 |
22. Связь напряжений и деформаций.
|
|
|
|
22. Связь напряжений и деформаций.
Часто возникает необходимость выразить напряжения через деформации. Решим уравнения обобщенного закона Гука относительно 
:
,
,
.
Пусть:
,
.
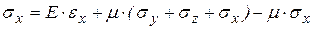Определим 
. Суммируя напряжения, получим:
,
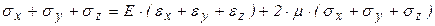или
,
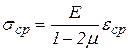где - 
, 
.
Тогда:
.
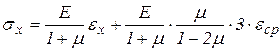Или
, 
;
, 
;
, 
.
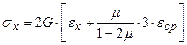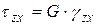Выражения также определяют запись обобщенного закона Гука для объемного напряженного состояния через деформации. Для нормальных напряжений можно записать:
; 
; 
,
где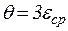 
(объемная деформация), 
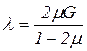(постоянная Ляме).
Определяя разность, имеем:
; 
;
.
Из последних соотношений определяется подобие кругов Мора для напряжений ( 
) и для деформаций (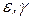 
). Применительно к «главному кубу», можно показать, что:
; 
; 
.
Получим упрощенную запись обобщенного закона Гука, используя выражение для обобщенного напряжения, действительно:
=
=
Учитывая, что:
Имеем:
.
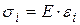Интенсивность напряжений прямо пропорциональна интенсивности деформаций. Если в процессе простого и сложного нагружения для каждого последующего момента времени интенсивность напряжения 
и интенсивность деформации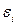 
превышают их значения для предыдущего момента времени, то такой процесс деформации называется активным. В противном случае – пассивным. Это имеет значение для теории пластичности, где имеет место различие законов нагрузки и законов разгрузки.
23. Постановка задачи теории упругости.
На базе изложенного теоретического материала появляется возможность спрогнозировать результат, определить напряженно-деформированное состояние в каждой точке очага деформации, т. е. рассчитать его. При этом отпадает необходимость производить многочисленные промежуточные преобразования и доказательства, а среди полученных конечных математических зависимостей выбрать те, которые необходимы для создания математической модели процесса упругого деформирования. К ним относятся: дифференциальные уравнения равновесия, физические уравнения связи напряжений и деформаций, геометрические соотношения или уравнения неразрывности деформаций, граничные или краевые условия задачи. В результате можно сформировать систему дифференциальных и алгебраических уравнений, которую называют постановочной системой уравнений теории упругости. Таким образом, имеем следующую постановку задачи теории упругости:
|
|
|
дифференциальные уравнения равновесия;
,
,
.
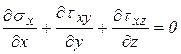физические уравнения связи напряжений и деформаций;
, 
;
, 
;
, .
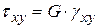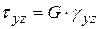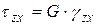дифференциальные уравнения неразрывности деформаций;
,
,
,
,
,
.
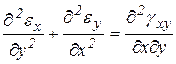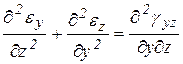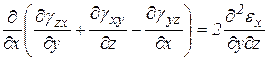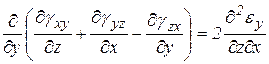граничные условия;
;
;
.
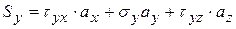Для решения задачи имеем 18 неизвестных и 18 уравнений теории упругости, включая граничные условия. Система статически определимая. Однако ее решение имеет большие математические трудности, что заставляет искать решения в упрощенном варианте. В представленной постановке задача считается замкнутой, т. к. решение должно удовлетворять уравнениям относящихся к напряжениям, так и деформациям. В противном случае задача считается не замкнутой. Последовательность решения следующая: Из уравнений равновесия определяются компоненты тензора напряжений, далее через физические уравнения связи - компоненты тензора деформаций, компоненты тензора деформаций должны удовлетворять уравнениям неразрывности деформаций.
|
|
|
