 |
19. Скорости деформаций. Тензор скоростей деформаций.
|
|
|
|
19. Скорости деформаций. Тензор скоростей деформаций.
При решении динамических задач теории пластичности и задач в условиях сложного нагружения пользуются теорией пластического течения, где вместо деформаций используются скорости деформаций. Рассмотрим этот деформационный параметр.
В процессе деформации материальные точки тела находятся в движении таким образом, что расстояние между ними изменяется. Чем быстрее изменяется расстояние между точками, тем больше скорость перемещения точки. Если деформации малы, то компоненты скоростей перемещений:
, 
, 
.
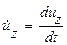Если существует предел отношения разности скоростей точек к расстоянию между ними при стремлении последней к нулю, тогда скорость деформации:
, 
,
или
, 
.
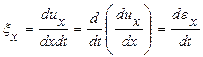
В итоге можно записать: скорости относительных удлинений и относительных сдвигов:
, 
;
, 
;
, 
.
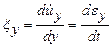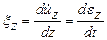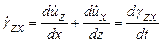Компоненты скоростей деформаций, образуют тензор скоростей деформаций
.
При пластической деформации объём тела не изменяется и тензор скоростей деформации является девиатором, следовательно 
.
Условие постоянства объема в деформациях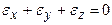 
, в скоростях деформаций 
.
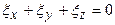Для скоростей деформации можно определить главные оси скоростей деформации, главные скорости сдвига, скорость октаэдрического сдвига, интенсивность скорости сдвига и интенсивность скоростей деформации. Тензор скоростей деформаций в главных координатах:
.
Интенсивность скоростей деформации сдвига и интенсивность скоростей деформаций
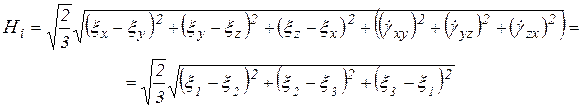
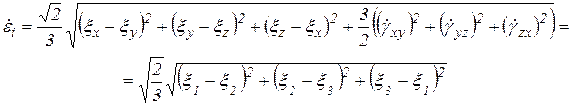Скорость октаэдрического сдвига
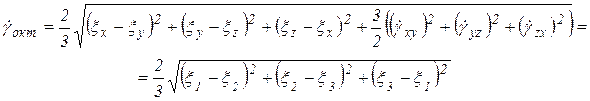Так же, как и для деформаций, последние величины характеризуют полностью скоростные и деформационные параметры материальной точки, т. к. под радикалом присутствуют все компоненты тензора скоростей деформаций.
|
|
|
20. Общая характеристика обобщенного закона упругости.
1. 3. Обобщенный закон упругости
1. 3. 1. Связь деформаций и напряжений для пространственного
напряженного состояния
Известна связь между напряжением и деформацией при одноосном напряженном состоянии, установленным Гуком:
,
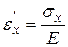где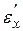 
- относительные удлинения параллелепипеда вдоль оси 
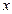под действием одного напряжения 
, 
– модуль упругости материала.
В направлении осе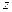й 
и 
, поперечных к действующей силе, имеет место деформация согласно закону Пуассона:
,
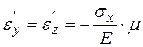где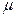 
- коэффициент Пуассона.
Соответственно для напряжени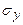й 
и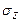 
имеем:
, 
,
, 
.
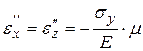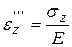Так как между напряжениями и деформациями линейная зависимость, то действует принцип суперпозиции или закон независимости действия сил, согласно которому:
; 
;
.
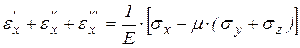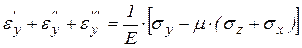Выражения предполагают, что не существует перекашивания прямых углов на гранях (углы сдвига) элементарного параллелепипеда.
Действие касательных напряжений искажают форму параллелепипеда. Принимается, что касательные напряжения или деформации сдвига не зависят от нормальных напряжений или линейных удлинений. Совокупность касательных напряжений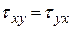 
, вызывает перекашивание граней, параллельных плоскости 
и оставляют без изменения другие грани. В соответствии со вторым законом Гука:
; 
,
где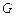 
– модуль упругости второго рода. Известно, что 
.
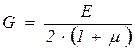От действия напряжений 
; 
,
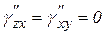от касательных напряжений 
; 
.
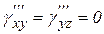Все компоненты напряжений определяют составляющие деформаций:
, 
;
, 
;
, .
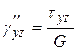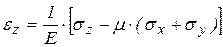Последние выражения представляют собой обобщенный закон упругости для изотропного тела.
Компоненты тензора деформаций в данной точке тела находятся в линейной зависимости от компонентов тензора напряжений в той же точке.
При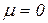 
компонент тензора напряжений прямо пропорционален соответствующему компоненту тензора деформации.
|
|
|
|
|
|
