 |
26. Характеристика гипотез наступления пластической деформации.
|
|
|
|
26. Характеристика гипотез наступления пластической деформации.
Критерий, который определяет условия возникновения пластической деформации при сложном напряженном состоянии, называется условием пластичности.
2. 2. 1. Первое предельное состояние
Рассмотрим одноосное напряженное состояние, в этом случае имеем нормальное растягивающее напряжение 
. На рис. 2. 1 представлена схема напряжений, действующих на наклонной площадке растягиваемого образца. Напряжения растяжения 
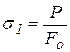. Напряжение на наклонной площадке:
, при этом 
,
,
.
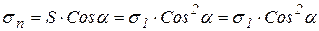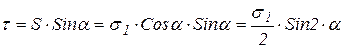Рисунок 2. 1 - Схема напряжений, действующих на наклонной площадке
Аналогичные формулы можно получить, используя выражения для нормальных и касательных напряжений на наклонной площадке при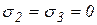 
.
Действительно:
, 
, 
.
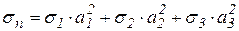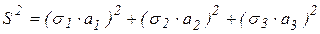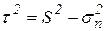При этом:
, 
, 
= 
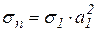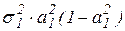
т. к.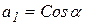 
, 
, тогда 
Пластическая деформация реализуется под действием максимальных касательных напряжений, т. е. при максимальном значении тригонометрической функции и максимальном значении напряжения 
, тогда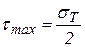 
, или: 
.
Последняя формула представляет первое предельное состояние при линейном напряженном состоянии.
Первое предельное состояние позволяет установить подходы реализации условия пластичности для объемного напряженного состояния, воспользовавшись гипотезой «единой кривой». В этом случае предполагается независимость вида уравнений от схемы напряженного состояния. В последнем выражении, с одной стороны предел текучести 
, зависящий от деформационных, скоростных и температурных факторов. С другой, величина, характеризующая напряженное состояние точки, в данном случае .
Гипотеза «единой кривой» позволяет поставить знак равенства между значениями, характеризующие объемное напряженное состояние и пределом текучести, полученного на основании опытных данных в условиях линейного растяжения или сжатия.
|
|
|
2. 2. 2. Условие пластичности Треска-Сен-Венана или условие
максимальных касательных напряжений
При объемном напряженном состоянии, кроме главного напряжения присутствуют еще напряжения, 
и 
. Какое сочетание главных напряжений определяет напряженное состояние точки? В общем, для определения условия пластичности, необходимо знать зависимость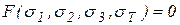 
.
Принимая положение о наступлении пластической деформации под действием максимальных касательных напряжений, следует рассмотреть напряжения на диагональных площадках, на которых касательные напряжения получают экстремальное значение и имеют вид:
, 
, 
.
Записывая соотношения 
, имеем максимальную разность и максимальные касательные напряжения 
. Выше было показано, что при линейном напряженном состоянии, когда 
, 
.
Используя гипотезу «единой кривой», запишем 
или 
, условие пластичности Треска – Сен-Венана.
Принципиальным отличием от условия первого предельного состояния заключается в том, что напряженное состояние точки определяется разностью главных нормальных напряжений, а не величиной одного главного напряжения .
В общем случае, напряженное состояние тела неоднородно, отсюда условие пластичности применяют для каждой точки деформируемой среды. Поэтому максимальные разности для отдельных точек могут меняться, тогда
, 
, 
.
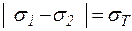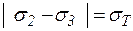Условие Треска – Сен-Венана имеет, в данной форме, наглядную геометрическую интерпретацию в координатах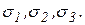 
Фигура представляет собой правильную шестигранную призму, ось которой проходит через начало координат, одинаково наклоненной к координатным направлениям. Поверхность призмы называется поверхностью пластичности. Если напряженное состояние определяется точкой расположенной внутри призмы пластичности, то тело находится в упругом состоянии, если на поверхности - тело находится в пластическом состоянии. Вне пределов призмы – смысла нет. Сечение поверхности пластичности плоскостью 
показано на рис. 2. 2.
|
|
|
Характерные точки 
- переход в предельное состояние при одноосном растяжении (сжатии). Точки 
- переход в предельное состояние при двухосном растяжении (сжатии).
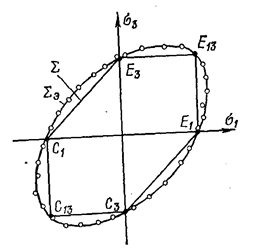
Рисунок 2. 2 - Сечение поверхности пластичности
|
|
|
