 |
27. Аналитическое решение плоской задачи теории упругости.
|
|
|
|
Выше приведенные теоретические материалы теории упругости можно использовать при постановке и решении задач теории упругости. В литературе рассматривается множество направлений и упрощений для прикладных вопросов механики сплошной среды. Одним из упрощений является использование плоской задачи вместо пространственной.
Постановка плоской задачи теории упругости включает уравнения равновесия, уравнение неразрывности деформаций и граничные условия. Уравнение неразрывности деформаций выражено через напряжения, за счет уравнений равновесия и закона Гука.
Имеем следующую постановку плоской задачи:
уравнения равновесия
уравнение неразрывности деформаций
,
граничные условия в напряжениях
,
где 
- среднее нормальное напряжение или гидростатическое давление.
Граничные условия в такой постановке вызывают вопросы. Их следует обозначить для дальнейших исследований. Используя выражение интенсивности касательных напряжений, для плоской задачи:
,
можно определить разность нормальных напряжений:
.
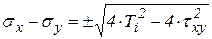При подстановке выражений в граничные условия, имеем:
,
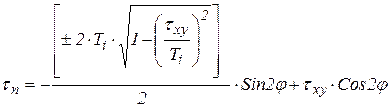В таком виде, задача не решается. Однако, используя тригонометрическую подстановку:
,
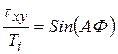задача с граничными условиями значительно упрощается:
,
где 
- функция координат очага деформации, совпадающая по функциональному назначению с интенсивностью касательных напряжений.; 
– постоянный коэффициент, определяющий упругое состояние деформируемой среды; 
- функция координат, характеризующая контактные касательные напряжения, одна из вводимых в рассмотрение аргумент функций; 
- угол наклона площадки.
|
|
|
Для линейных дифференциальных уравнений в частных производных принимается экспоненциальная подстановка вида:
,
где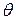 
- неизвестная и вторая аргумент функция.
Тогда касательные напряжения и разности нормальных напряжений запишутся:
,
.
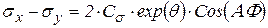При подстановке касательных напряжений в уравнение равновесия, получим:
, 
.
Записывая конечный результат интегрирования задачи, в конечном виде имеем:
,
.
,
при условии
, 
.
, 
.
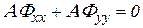Дифференциальные соотношения между аргумент функциями представляют собой соотношения Коши-Римана и уравнения Лапласа. Функции, удовлетворяющие уравнениям Лапласа, называются гармоническими.
Анализируя выражения для нормальных напряжений, убеждаемся в том, что задача еще не решена, т. к. неизвестны значения средних нормальных напряжений. Для их определения воспользуемся уравнением неразрывности деформаций, в виде:
,
где 
.
Такое выражение принято на основании того, что в формулах для нормальных напряжений эта зависимость является определяющей. Для того, что бы решить уравнение Лапласа необходимо взять производные по координатам и подставить в уравнение. После подстановки имеем два оператора, вида:
+ 
=0.
где 
- мнимая единица.
Если будет доказано, что оба оператора равны нулю тогда уравнение Лапласа превращается в тождество, и среднее напряжение считается определенным. При этом должно выполняться условие существование решения:
, .
, .
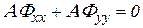В итоге решение плоской задачи теории упругости имеет вид:
,
.
,
,
при условии
, .
, .
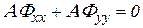Для достоверности полученного результата протестируем выражения на конкретном практическом примере. Покажем влияние их построения на распределение контактных напряжений в упругой зоне. Исследуем напряженное состояние упругого полупространства под действием силы P массивного штампа, шириной 2b, (рис. 4. 5).
|
|
|
Рисунок 4. 5 - Действие плоского штампа на упругое полупространство
На контакте отсутствуют касательные напряжения. В реальных условиях задача может отнестись к геомеханике. Представляет интерес нагружение слоев грунта под действием массивных сооружений. В результате подстановки граничных условий окончательно имеет расчетные значения формул:
,
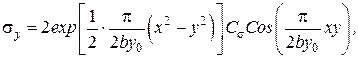
где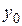 
– положение точки в глубине полуплоскости в случае экстремального значения тригонометрической функции. Если задать положение на контакте, т. е. y=0:
.
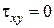Видно, что экстремальные значения тригонометрических функций находятся не только на контакте, но и в глубине полупространства.
На рис. 4. 6 показано распределение нормальных напряжений на контакте и в глубине полупространства. Графики выполнены с использованием относительных величин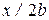 
и 
где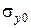 
– минимальное значение нормальных напряжений в зоне деформации.
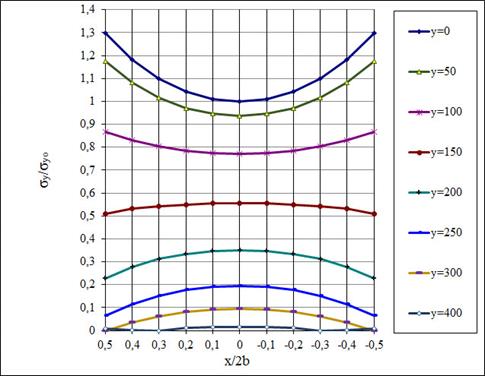
Рисунок 4. 3 - Распределение нормальных напряжений на контакте и в глубине полупространства при действии плоского штампа без учета трения.
Особенностью данного решения является затухание поверхностного воздействия по мере увеличения вертикальной координаты, т. е. глубины пространства. В пределе напряжения равны нулю. Полученные расчетные данные соответствуют реальному распределению напряжений вдоль и поперек внешнего нагружения.
|
|
|
