 |
28. Аналитическое решение плоской задачи теории пластичности.
|
|
|
|
28. Аналитическое решение плоской задачи теории пластичности.
Предлагается решение плоской задачи теории пластичности с использованием современного метода решения задач механики сплошной среды - метода аргумент функций.
Задача решается в напряжениях без привлечения деформационной составляющей. Привлекаются уравнения равновесия, обобщенное уравнение равновесия и граничные условия в напряжениях. Уравнение Прандтля имеет вид:
,
где 
- интенсивность касательных напряжений.
Используя тригонометрическую подстановку, удается линеаризировать уравнение Прандтля, имеем:
, 
.
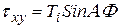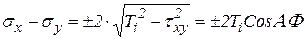где 
- неизвестная функция или первая аргумент функция. Граничные условия имеет вид:
.
где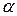 
- угол наклона площадки.
Используется фундаментальная подстановка с привлечением второй аргумент функций, вида:
,
определяется функциональная зависимость вида
.
Подставляя касательные напряжения в уравнения равновесия, интегрируя, получим:
, 
,
,
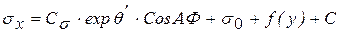при выполнении соотношений Коши-Римана:
, 
,
и уравнений Лапласа:
, 
.
С использованием полученных решений рассмотрим задачу осадки полосы на шероховатых бойках. Для более полного удовлетворения граничных условий, искомые функции можно представить в виде суммы гармонических функций, т. е.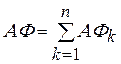 
, 
. Тогда из уравнений Лапласа и соотношений Коши-Римана определяем аргумент функции, имеем:
,
.
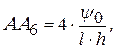
В выражениях постоянные величины определялись из реальных граничных услови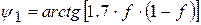й:
,
, 
,
и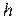 
- длина, и высота очага деформации при осадке полосы, 
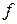- коэффициент трения. Коэффициент:
,
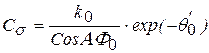при этом:
,
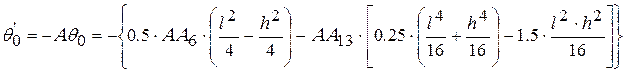
Имеем рабочие формулы для расчета контактных напряжений при осадке на шероховатых бойках:
|
|
|
, 
,
.
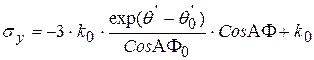На рис. 2. 3 и 2. 4 представлено распределение нормальных и касательных напряжений на контакте полосы при разных значениях фактора формы 
и коэффициента трения . Анализ вычислений по выражениям показывает, что решения плоской задачи реагирует на технологические параметры процесса, т. е. коэффициент трения и фактор формы.
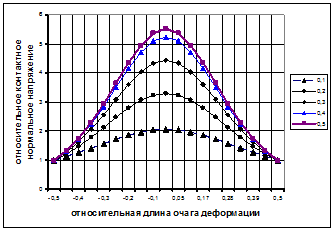
Рисунок 2. 4 - Распределение нормальных и касательных напряжений на контакте при осадке на шероховатых бойках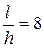 
, 
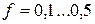
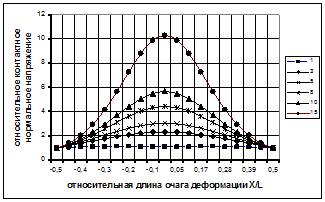
Рисунок 2. 5 - Распределение нормальных и касательных напряжений на контакте при осадке на шероховатых бойках 
, 
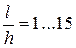
С увеличением коэффициента трения растут контактные нормальные и касательные напряжения. При этом наблюдается ограничение роста с увеличением коэффициента трения. Фактор формы очага деформации оказывает существенное влияние на величину и характер распределения напряжений по длине очага деформации. При этом получены простые выражения для расчета, единые для всего очага деформации.
29. Условие пластичности Губера-Мизеса.
Недостатком условия пластичности Треска - Сен-Венана является отсутствие учета в напряженном состоянии точки среднего главного напряжения 
.
Обобщенной характеристикой напряженного состояния можно считать октаэдрическое касательное напряжение 
, с учетом запишем:
.
При линейном напряженном состоянии, с учетом первого предельного состояния, октаэдрическое касательное напряжение равно 
.
Воспользуемся гипотезой «единой кривой», тогда:
= 
,
или
= 
.
В левой части интенсивность касательных напряжений в главных координатах, т. е. 
. В произвольных координатах:
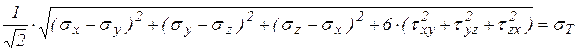
Последние три равенства представляют собой условие пластичности Губера-Мизеса, которое формулируется следующим образом: предельное состояние пластичности наступит тогда, когда интенсивность напряжений при объемном напряженном состоянии достигнет предела текучести. При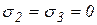 
имеем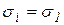 
, т. е. переходим к первому предельному состоянию в условиях линейного напряженного состояния 
.
|
|
|
Условие Губера-Мизеса в литературе имеет несколько наименований:
- условие постоянства интенсивности напряжений;
- условие постоянства октаэдрического касательного напряжения;
- условие постоянства удельной энергии изменения формы или «энергетическое условие».
Условие Губера-Мизеса имеет геометрическую интерпретацию. Поверхность пластичности отображается цилиндрической поверхностью, ось которой одинаково наклонена к направлениям 
Сечение поверхности пластичности плоскостью 
, называется контуром пластичности и имеет вид эллипса, рис. 2. 2. В точках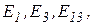 
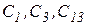условие пластичности Губера-Мизеса и Треска - Сен-Венана дают одинаковый результат. Представляет интерес определение напряжений 
, и 
таким образом, чтобы они удовлетворяли условие пластичности. Показано, что главные напряжения могут тождественно удовлетворить уравнение пластичности при условии:
, 
, 
где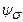 
- угол вида напряженного состояния. Подставляя напряжения в условия пластичности, получим тождество.
|
|
|
