 |
Основные аффинные и метрические задачи
|
|
|
|
Раздел 1_3 - Метод координат
На плоскости и в пространстве
Лекция 7
Аффинная и прямоугольная декартова
Системы координат
Понятие аффинной и прямоугольной декартовой
Систем координат
| О |

|
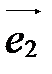
|
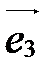
|
| Рис. 31 |
| О |

|
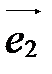
|
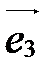
|
| х |
| у |
| z |
| Рис. 32 |
 ,
, 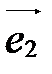 ,
, 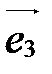 в пространстве, называется аффинной системой координат в пространстве и обозначается
в пространстве, называется аффинной системой координат в пространстве и обозначается  или
или 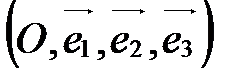 (рис. 31).
(рис. 31).
Точка О называется началом координат, векторы 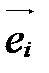 ,
, 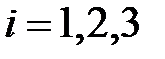 , - координатными векторами:
, - координатными векторами:  - первый координатный вектор,
- первый координатный вектор, 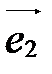 - второй,
- второй, 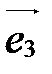 - третий.
- третий.
Направленные прямые, на которых положительное направление определяется базисными векторами и которые проходят через точку О, называются координатными осями:
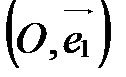 - ось абсцисс;
- ось абсцисс;
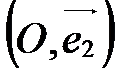 - ось ординат;
- ось ординат;
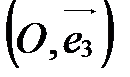 - ось аппликат (рис. 32).
- ось аппликат (рис. 32).
Оси абсцисс, ординат и аппликат обозначаются и так: Ох, Оу, О z.
Плоскости, определяемые осями Ох и Оу, Оу и О z, Ох и О z, называются координатными плоскостями и обозначаются Оху, Оу z, Oxz, а систему координат  иногда обозначают Oxyz.
иногда обозначают Oxyz.
| Рис. 33 |

|
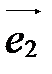
|
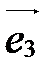
|
| О |
| М |
 - аффинная система координат, М – произвольная точка пространства. Вектор
- аффинная система координат, М – произвольная точка пространства. Вектор 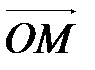 называется радиус-вектором точки М относительно точки О (рис. 33).
называется радиус-вектором точки М относительно точки О (рис. 33).
Понятие координат точки вводится на основе понятия координат вектора.
Координатами точки М в системе координат  называются координаты ее радиус-вектора
называются координаты ее радиус-вектора 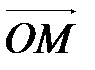 в базисе
в базисе  ,
, 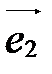 ,
, 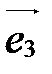 .
.
Обозначение  или просто М(х;у; z): х – абсцисса точки М, у – ордината, z – аппликата.
или просто М(х;у; z): х – абсцисса точки М, у – ордината, z – аппликата.
Если в пространстве задана аффинная система координат, то устанавливается взаимно однозначное соответствие между точками пространства и упорядоченными тройками (х;у; z) действительных чисел.
|
|
|
Рассмотрим особенности расположения точки относительно аффинной системы координат, если некоторые ее координаты являются нулевыми. Пусть М(х;у; z).
1) Если z =0, то М(х;у;0) Þ 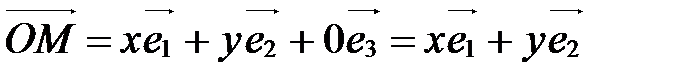 Þ
Þ 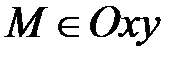 . Верно и обратное:
. Верно и обратное: 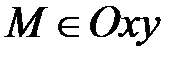 Þ z =0.
Þ z =0.
2) Докажите самостоятельно, что если у=0, то  , и наоборот, если
, и наоборот, если  , то у=0.
, то у=0.
3) Докажите самостоятельно, что если х=0, то 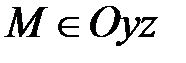 , и наоборот, если
, и наоборот, если 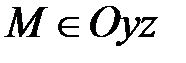 , то х=0.
, то х=0.
4) Если z =0 и у=0, то 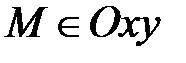 и
и  Þ
Þ 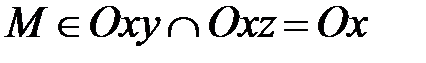 Þ
Þ 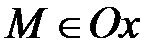 . Верно и обратное:
. Верно и обратное: 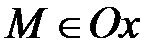 Þ z =0 и у=0.
Þ z =0 и у=0.
Докажите самостоятельно, что:
5) Если х =0 и у=0, то 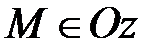 и наоборот, если
и наоборот, если  , то х =0 и у=0.
, то х =0 и у=0.
6) Если х =0 и z =0, то 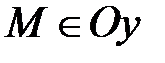 и наоборот, если
и наоборот, если 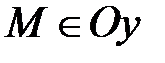 , то х =0 и z =0.
, то х =0 и z =0.
7) Так как 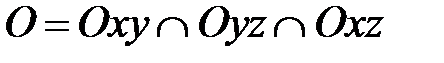 , то из пунктов 1) – 3) следует, что О (0;0;0) в системе координат
, то из пунктов 1) – 3) следует, что О (0;0;0) в системе координат 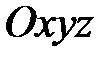 .
.
Чтобы построить точку М(х;у; z) по ее координатам в системе координат  , надо сначала построить точку М1 (х;0;0), затем точку М2 (х;у;0), а затем точку М (х;у;z). Процесс построения этих точек показан на рис. 34. Ломаная ОМ1М2М называется координатной ломаной точки М.
, надо сначала построить точку М1 (х;0;0), затем точку М2 (х;у;0), а затем точку М (х;у;z). Процесс построения этих точек показан на рис. 34. Ломаная ОМ1М2М называется координатной ломаной точки М.
| М1 |
| М |
| М2 |
| О |

|

|

|
| Рис. 34 |
 или
или 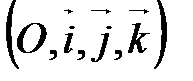 , где
, где 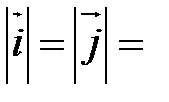
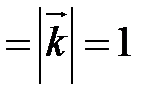 ,
, 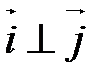 ,
, 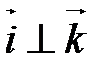 и
и 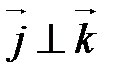 .
.
Прямоугольная декартова система координат является частным случаем аффинной.
Замечание. На плоскости аффинная система координат состоит из точки О (начала координат) и двух базисных векторов  и
и 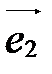 (координатных векторов) (рис. 35). Поэтому в системе координат на плоскости любая точка имеет две координаты
(координатных векторов) (рис. 35). Поэтому в системе координат на плоскости любая точка имеет две координаты 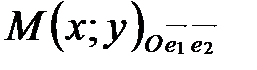 . Прямоугольная декартова система координат на плоскости изображена на рис. 36.
. Прямоугольная декартова система координат на плоскости изображена на рис. 36.
| О |
| О |

|
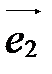
|
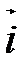
|
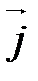
|
| Рис. 35 |
| Рис. 36 |
Задания для самостоятельной работы
1. Известны координаты точки М (-2;1;0) в аффинной системе координат  . Каковы координаты точки М в системе координат
. Каковы координаты точки М в системе координат 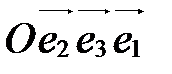 ?
?
2. Дано изображение аффинной системы координат  . Постройте точки Р (0;-2;0), Q (0;-3;-1), N (-1;2;-4).
. Постройте точки Р (0;-2;0), Q (0;-3;-1), N (-1;2;-4).
|
|
|
3. М – центр тяжести (точка пересечения медиан) треугольника АВС. Найдите координаты точки В в системе координат 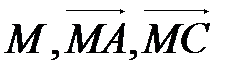 , не достраивая треугольник АМС до параллелограмма.
, не достраивая треугольник АМС до параллелограмма.
4. Докажите, пользуясь определением координат точки, что если соответственные (одноименные) координаты двух точек равны, то эти точки совпадают.
Основные аффинные и метрические задачи
Задача называется метрической, если в ней фигурируют метрические свойства фигур, т.е. свойства, которые можно выявить непосредственным измерением (длина отрезка, расстояние между точками, расстояние от точки до прямой или плоскости, величина угла, перпендикулярность, площадь, объем). В аффинных задачах метрические свойства не рассматриваются. Аффинные задачи решаются в аффинной системе координат, а, следовательно, и в прямоугольной декартовой. Метрические задачи удобно решать в прямоугольной системе координат.
Основные аффинные и метрические задачи, решаемые с помощью координат, сформулируем в виде теорем.
Основные аффинные задачи
1. Координаты вектора, заданного двумя точками.
Теорема 1. Если в аффинной системе координат 
 и
и  , то
, то  .
.
Представим вектор 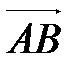 в виде разности векторов
в виде разности векторов 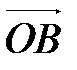 и
и 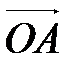 :
:
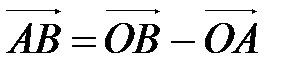 .
.
Так как  , то по определению координат точки
, то по определению координат точки 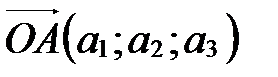 . Аналогично
. Аналогично 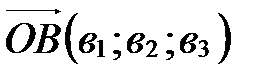 . Применяя свойство координат векторов (координаты разности двух векторов равны разности их соответствующих координат), получаем, что вектор
. Применяя свойство координат векторов (координаты разности двух векторов равны разности их соответствующих координат), получаем, что вектор 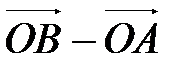 имеет координаты
имеет координаты 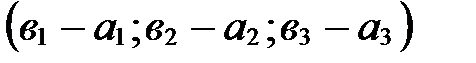 Þ
Þ  .
.
2. Деление отрезка в данном отношении.
Говорят, что точка М делит направленный отрезок 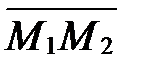 в отношении
в отношении 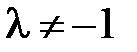 , если выполняется векторное равенство:
, если выполняется векторное равенство:
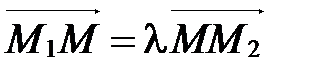 . (1)
. (1)
Число 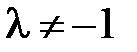 при этом называется простым отношением трех точек М1, М2 и М. Простое отношение трех точек М1, М2 и М обозначается так:
при этом называется простым отношением трех точек М1, М2 и М. Простое отношение трех точек М1, М2 и М обозначается так: 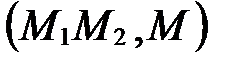 .
.
Почему в определении деления отрезка в данном отношении 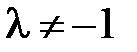 ?
?
Пусть М1 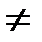 М2 и точка М делит направленный отрезок
М2 и точка М делит направленный отрезок 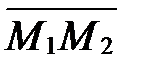 в отношении l=-1. Тогда по определению деления отрезка в данном отношении
в отношении l=-1. Тогда по определению деления отрезка в данном отношении
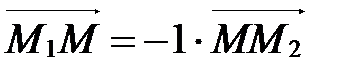 ,
,
т.е. 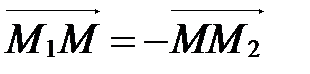 Þ
Þ 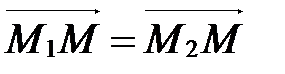 Þ
Þ  . А так как начало у векторов
. А так как начало у векторов 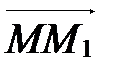 и
и 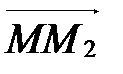 общее и они равны, то М1=М2. Получили противоречие с условием, следовательно,
общее и они равны, то М1=М2. Получили противоречие с условием, следовательно, 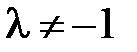 .
.
Из векторного равенства (1) следует, что если 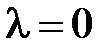 , то
, то 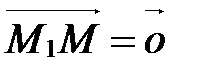 , т.е. точка М совпадает с точкой М1; если l>0, то точка М лежит внутри отрезка
, т.е. точка М совпадает с точкой М1; если l>0, то точка М лежит внутри отрезка 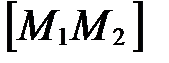 (рис. 37), т.е.
(рис. 37), т.е. 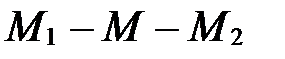 ; если l<0, то точка М лежит на прямой
; если l<0, то точка М лежит на прямой 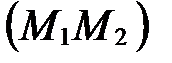 вне отрезка
вне отрезка 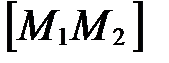 (рис. 38), т.е.
(рис. 38), т.е. 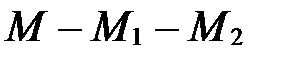 или
или 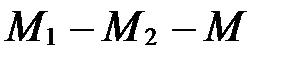 .
.
|
|
|
| М1 |
| М |
| М2 |
| Рис. 37 |
| М |
| М1 |
| М2 |
| М2 |
| М1 |
| М |
| Рис. 38 |
Теорема 2. Пусть в аффинной системе координат 
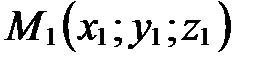 ,
, 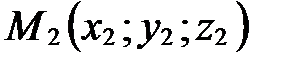 . Тогда координаты точки
. Тогда координаты точки 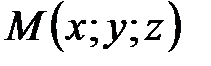 , делящей направленный отрезок
, делящей направленный отрезок 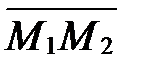 в отношении
в отношении 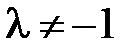 , находятся по формулам:
, находятся по формулам:
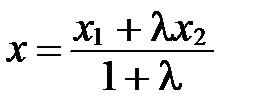 ;
; 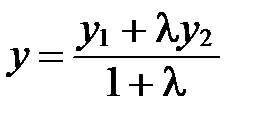 ;
; 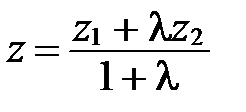 . (2)
. (2)
По определению деления отрезка в данном отношении 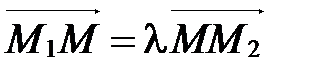 .
.
| О |

|
|
|
| М1 |
| М |
| М2 |
| Рис. 39 |
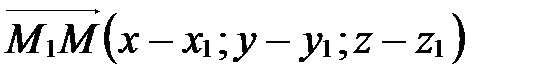 ,
, 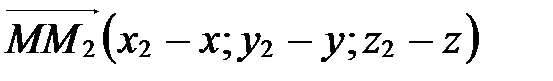 . Тогда
. Тогда 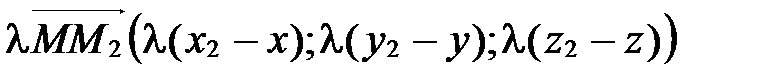 . Так как два вектора равны тогда и только тогда, когда равны их соответствующие координаты, то
. Так как два вектора равны тогда и только тогда, когда равны их соответствующие координаты, то 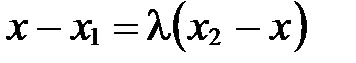 ;
; 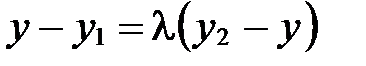 ;
; 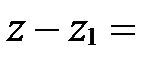
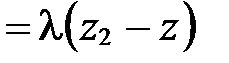 , откуда получаем:
, откуда получаем: 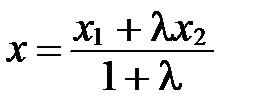 ;
; 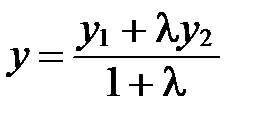 ;
; 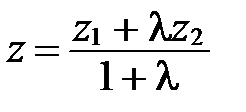 .
.
Формулы (2) называются формулами деления отрезка в данном отношении в координатах.
Из теоремы 2 получаем
Следствие. Если М(х;у; z) – середина отрезка М1М2 с концами 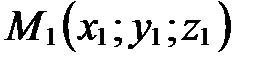 и
и 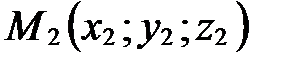 , то
, то 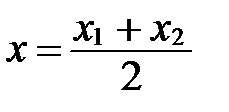 ,
, 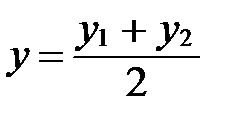 ,
,  .
.
Так как М – середина М1М2, то 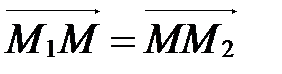 Þ l=1. Применяя формулы деления отрезка в данном отношении в координатах, получаем:
Þ l=1. Применяя формулы деления отрезка в данном отношении в координатах, получаем:
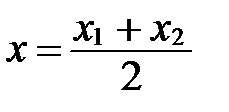 ,
, 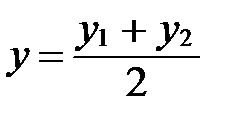 ,
,  .
.
|
|
|


