 |
Задания для самостоятельной работы
|
|
|
|
1. Приведите уравнение гиперболы к каноническому виду:
а)  ;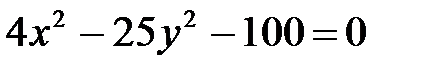
| в)  ;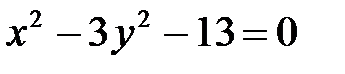
|
б)  ;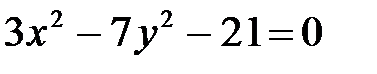
| г)  .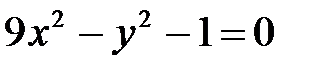
|
2. Дано каноническое уравнение гиперболы. Найдите действительную и мнимую «полуоси», координаты вершин, координаты фокусов, фокальное расстояние, фокальные радиусы точки 
, эксцентриситет, уравнения директрис:
а)  ;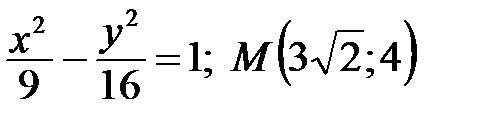
|
б)  .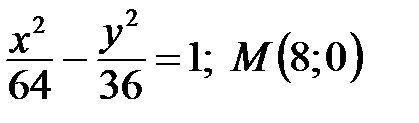
|
3. Постройте изображение гиперболы, ее фокусов и директрис:
а)  ;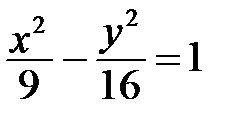
| б)  .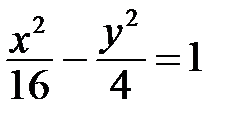
|
4. Докажите, что эксцентриситет равносторонней гиперболы равен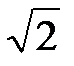 
.
Парабола
Параболой называется множество всех точек плоскости, расстояние каждой из которых до данной точки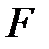 
равно расстоянию до данной прямой 
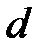, не содержащей точку .
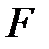Точка 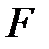называется фокусом параболы, а прямая 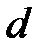- директрисой.
Расстояние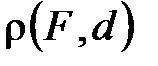 
от фокуса до директрисы называется фокальным параметром параболы и обозначается через 
:
.
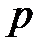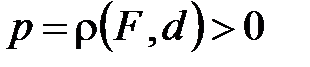Коротко определение параболы 
можно записать так:
.
|
|
|
|
|
|
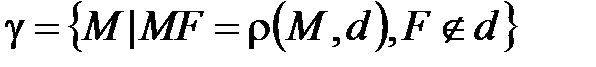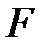
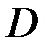
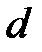
| Рис. 95 |
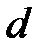и точка 
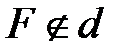. Проведем из точки 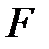перпендикуляр 
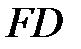к прямой 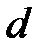. Выберем прямоугольную декартову систему координат 
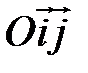так, чтобы точка 
была серединой отрезк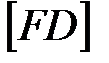а 
, а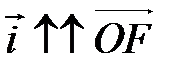 
(рис. 95).
Выведем уравнение параболы с фокусом 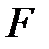и директрисой 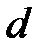в системе координат .
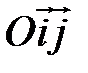Найдем координаты точки 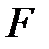и прямой 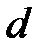в системе : 
.
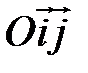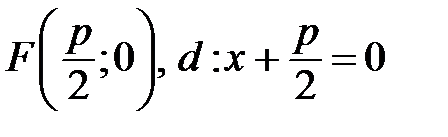Пусть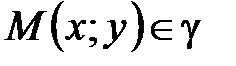 
. Тогда по определению параболы 
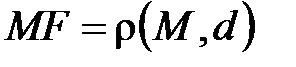. Учитывая, что 
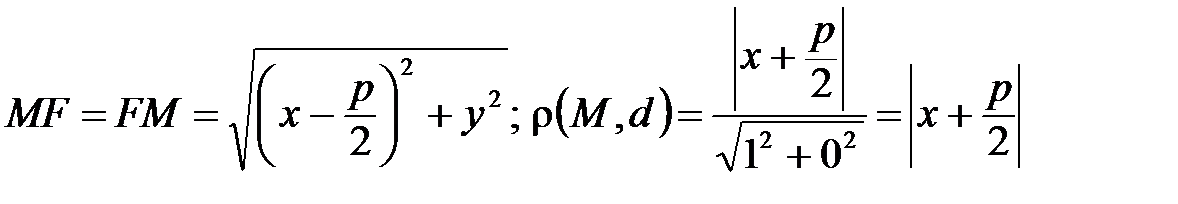, получим:
.
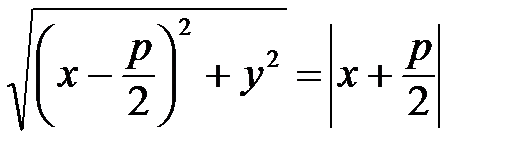Преобразуем это уравнение:
;
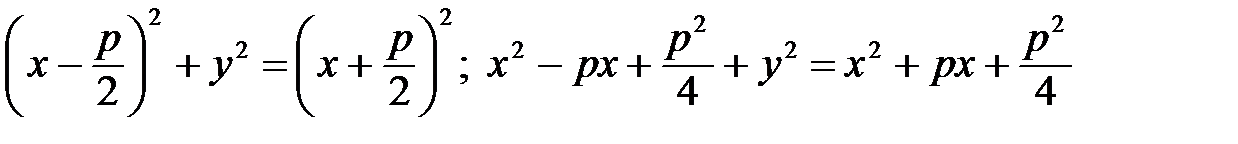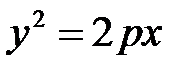. (42)
Итак, если точка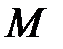 
принадлежит параболе , то ее координаты удовлетворяют уравнению (42).
Пусть, обратно, координаты точки 
удовлетворяют уравнению (42), т.е.
.
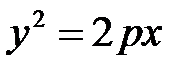Тогд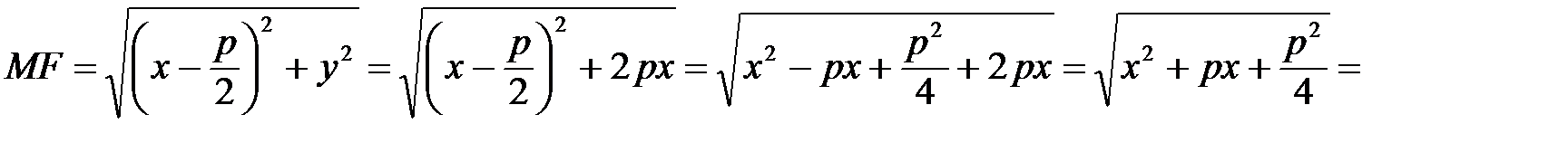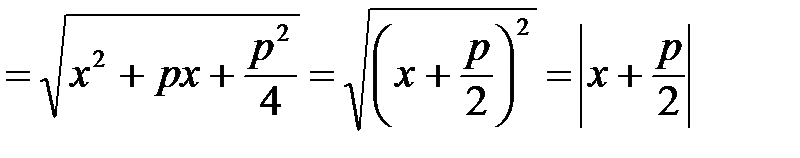а 
; а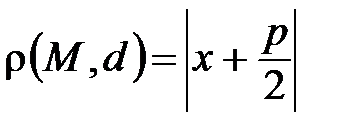 
. Следовательно, 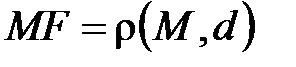, т.е. 
(по определению параболы).
|
|
|
Таким образом, доказано, что уравнение (42) есть уравнение параболы с фокусом 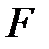и директрисой 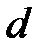. Уравнение (42) называется каноническим уравнением параболы.
Чтобы изобразить параболу по ее каноническому уравнению, исследуем геометрические свойства параболы.
Свойства параболы
1°. Так как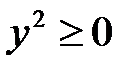 
и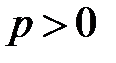 
, то из уравнения (42) следует, что 
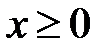, т.е. все точки параболы принадлежат полуплоскости .
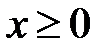2°. Выясним, симметрична ли парабола 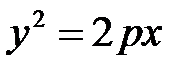относительно начала координат и осей координат.
Пусть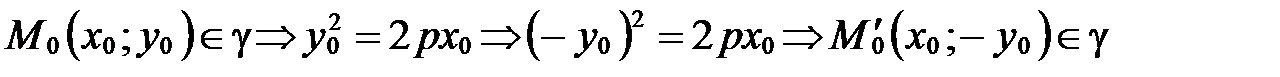 
, т.е. парабола симметрична относительно оси 
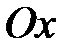. Ось симметрии параболы называется осью параболы.
Заметим, что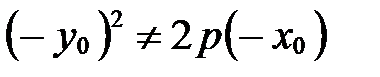 
и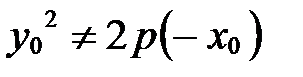 
, следовательно, 
и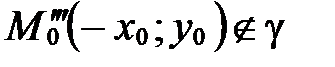 
, т.е. парабола не симметрична относительно начала координат и оси 
.
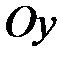3°. Найдем точки пересечения параболы с осями координат.
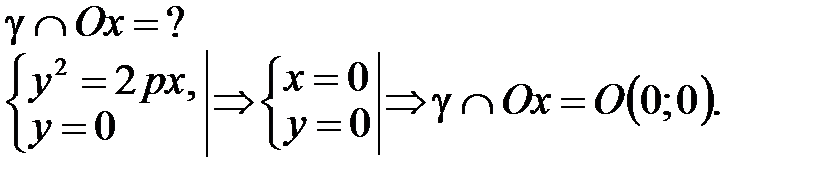
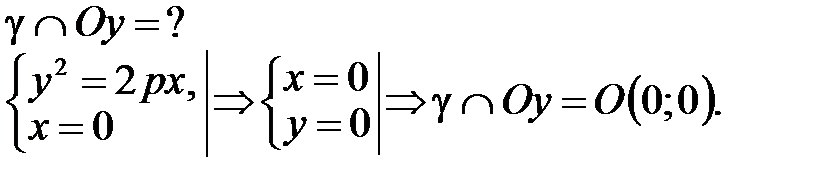
Таким образом, парабола имеет одну вершину.
4°. Зависимость формы параболы от ее фокального параметра.
Чем больше фокальный параметр 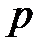, тем сильнее парабола вытягивается вдоль оси .
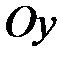5°. Чтобы изобразить параболу, найдем координаты четырех вспомогательных точек, принадлежащих параболе.
.
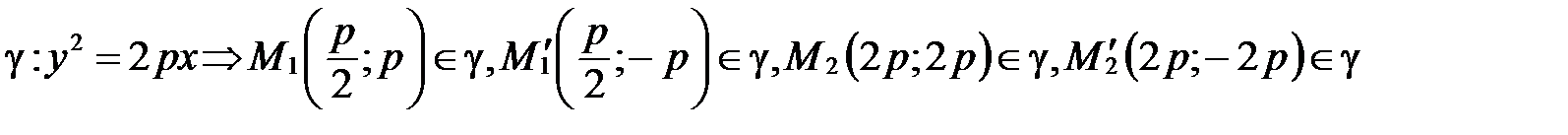Построение изображения параболы по ее каноническому уравнению выполняется в следующей последовательности: выбираем на плоскости прямоугольную декартову систему координат 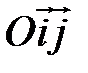; строим точки 
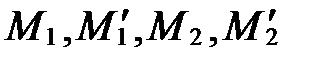; проводим через точки 
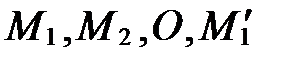и 
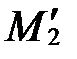параболу; строим фокус 
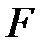и директрису 
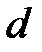(рис. 96).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
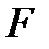
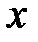
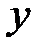
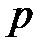
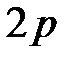
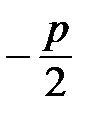
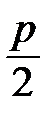
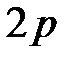
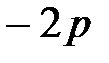
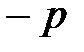
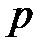
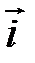
| Рис. 96 |
Эксцентриситетом параболы называется число единица.
Из определения параболы следует, что 
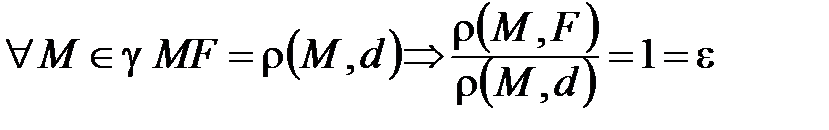, т.е. для параболы также имеет место директориальное свойство.
Директриса параболы также никогда не пересекает параболу.
Если построить параболы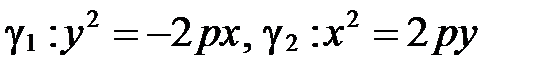 
и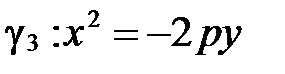 
в той же канонической системе координат 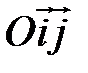, то они будут расположены так (рис. 97):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
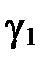
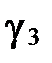
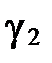
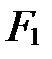
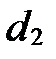
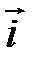
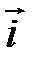
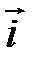
| Рис. 97 |
|
|
|
Заметим, что на ось параболы в ее каноническом уравнении указывает та переменная, которая стоит в первой степени.
Задания для самостоятельной работы
1. Приведите к каноническому виду уравнение параболы:
а)  ;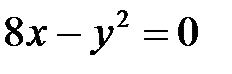
| г)  ;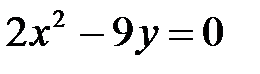
|
б)  ;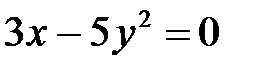
| д)  ;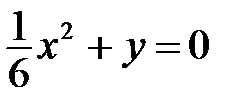
|
в)  ;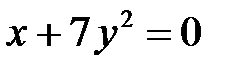
| е)  .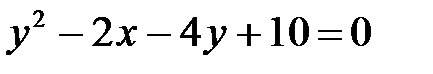
|
2. Дано каноническое уравнение параболы. Найдите фокальный параметр параболы, координаты фокуса и уравнение директрисы:
а)  ;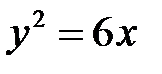
| в)  ;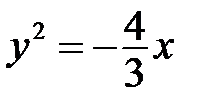
|
б)  ;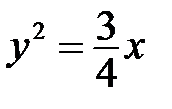
| г)  .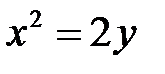
|
3. Изобразите параболу, ее фокус и директрису:
а)  ;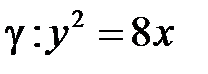
| в)  ;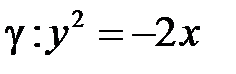
|
б)  ;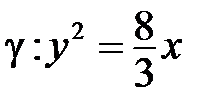
| г)  .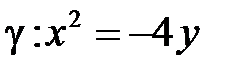
|
Лекция 15
Понятие о классификации линий второго порядка.
Приведение общего уравнения линии второго
|
|
|
