 |
Основная метрическая задача
|
|
|
|
Теорема 3(расстояние между двумя точками в координатах). Если в прямоугольной декартовой системе координат 
 ,
,  , то расстояние АВ между точками А и В находится по формуле:
, то расстояние АВ между точками А и В находится по формуле:
 .
.
Учитывая, что  ,
,  и используя формулы для нахождения длины вектора в координатах, получаем:
и используя формулы для нахождения длины вектора в координатах, получаем:
 .
.
Формулы, доказанные в теоремах 1 и 2, можно использовать и в аффинной, и в прямоугольной декартовой системе координат, а формулу из теоремы 3 – только в прямоугольной декартовой системе координат.
Задания для самостоятельной работы
1. Найдите координаты точки А, если В (3;0;-2),  .
.
2. С – середина отрезка АВ. Найдите координаты точки В, если А (1;0;-4), С (3;1;0).
3. Точки Р и Q лежат внутри отрезка АВ, причем АР=Р Q = Q В. Найдите (В Q,А).
4. На плоскости дан отрезок [АВ]. Постройте точку С, делящую направленный отрезок  в отношении
в отношении  ;
;  .
.
5. Известны координаты вершин треугольника АВС: А(4;3), В(0;5),С(-2;2). Пользуясь теоремой, обратной теореме Пифагора, выясните, будет ли этот треугольник прямоугольным.
6. Можно ли вывести формулы для нахождения расстояния между двумя точками, координаты которых даны в аффинной системе координат?
Раздел 1_4 - Формулы преобразования координат
Преобразование аффинной системы координат
Возьмем на плоскости две аффинные системы координат 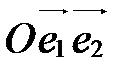 и
и  . Первую назовем старой, вторую - новой. Пусть М – произвольная точка плоскости, которая в старой системе
. Первую назовем старой, вторую - новой. Пусть М – произвольная точка плоскости, которая в старой системе 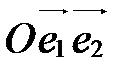 имеет координаты х,у, а в новой системе
имеет координаты х,у, а в новой системе  - координаты
- координаты  (рис. 40).
(рис. 40).
| О |
| О' |
| М |

|

|

|

|
| Рис. 40 |
 ,
,  ,
,  , (3)
, (3)
выразить координаты х,у точки М в старой системе координат, через координаты  этой точки в новой системе.
этой точки в новой системе.
|
|
|
Из формул (3) следует, что
 ;
;  ;
;  . (4)
. (4)
 (по правилу треугольника).
(по правилу треугольника).
Так как  ,
,  , то по определению координат точки
, то по определению координат точки 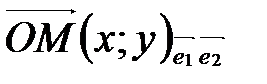 ,
,  , т.е.
, т.е.  ;
;  .
.
Тогда, используя формулы (4), получим:
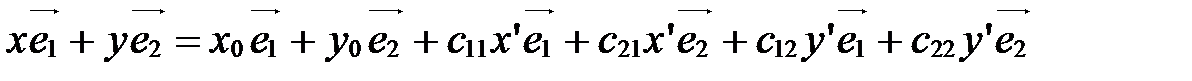 ,
,
т.е.  ,
,
откуда находим:
 ; ;
|
. Так выражаются координаты х,у произвольной точки М в старой системе 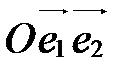 через ее координаты
через ее координаты  в новой системе
в новой системе  .
.
Формулы (5) называются формулами преобразования аффинной системы координат.
Коэффициенты 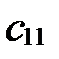 ,
,  при
при 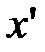 - координаты нового вектора
- координаты нового вектора  в старой системе
в старой системе 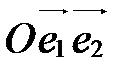 ; коэффициенты
; коэффициенты  ,
,  при
при  - координаты нового вектора
- координаты нового вектора 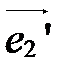 в старой системе, свободные члены
в старой системе, свободные члены  ,
,  - координаты нового начала
- координаты нового начала  в старой системе:
в старой системе:
Координаты точки М
в новой системе 
| х |
| у |
| = |
| = |
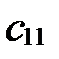
|

|

|

|
| + |
| + |

|
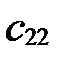
|

|

|
| + |
| + |

|

|
Координаты точки М в старой системе 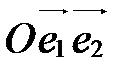
|
Координаты нового вектора  в старой системе в старой системе 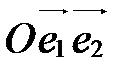
|
Координаты нового вектора 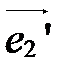 в старой системе в старой системе 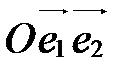
|
Координаты нового начала  в старой системе в старой системе 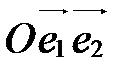
|
Таблица  называется матрицей перехода от базиса
называется матрицей перехода от базиса  ,
, 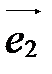 к базису
к базису  ,
,  .
.
Частные случаи преобразования аффинной
Системы координат
1. Перенос начала.
При этом преобразовании  ,
,  , а
, а  (рис. 41).
(рис. 41).
Найдем координаты векторов  и
и  в старой системе, т.е.
в старой системе, т.е. 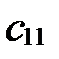 ,
,  ,
,  и
и  :
:
 Þ
Þ  Þ
Þ  ,
,  ;
;
 Þ
Þ  Þ
Þ  ,
,  .
.
Тогда формулы (5) примут вид:
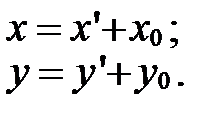
|
| (6) |
Формулы (6) называются формулами переноса начала.
| О |
| О' |

|

|

|

|
| Рис. 41 |

|

|

|

|
| О'=О |
| Рис. 42 |
2. Замена координатных векторов.
При этом преобразовании системы координат имеют общее начало и отличаются координатными векторами (рис. 42).
Так как  , то
, то  ,
,  . Тогда формулы (5) примут вид:
. Тогда формулы (5) примут вид:
|
|
|
 ; ;
 . .
|
| (7) |
Формулы (7) называются формулами замены координатных векторов.
Задания для самостоятельной работы
1. Напишите формулы преобразования аффинной системы координат 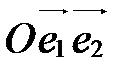 в аффинную систему координат
в аффинную систему координат  , если
, если  ,
,  ,
,  в системе
в системе 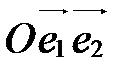 .
.
2. Может ли матрица перехода от базиса  ,
, 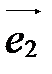 к базису
к базису  ,
,  иметь вид
иметь вид  и почему?
и почему?
3. Напишите формулы переноса начала, если  в системе координат
в системе координат 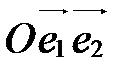 .
.
4. Напишите формулы замены координатных векторов, если  ,
, 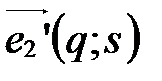 .
.
5. Запишите матрицу перехода от базиса  ,
, 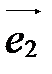 к базису
к базису  ,
,  в случае:
в случае:
а) переноса начала;
б) замены координатных векторов.
Понятие направленного угла между векторами.
|
|
|



