Преобразование прямоугольной системы координат
Понятие направленного угла между векторами вводится на ориентированной плоскости.
Пусть  и
и  - ненулевые векторы, заданные в определенном порядке (
- ненулевые векторы, заданные в определенном порядке ( - первый вектор,
- первый вектор,  - второй вектор).
- второй вектор).
Если  ||
||  , то направленным углом между вектором
, то направленным углом между вектором  и вектором
и вектором  называется
называется
величина  , если базис
, если базис  ,
,  - правый;
- правый;
величина  , если базис
, если базис  ,
,  - левый.
- левый.
Если  , то направленный угол между ними считается равным
, то направленный угол между ними считается равным  , если
, если  , то
, то  (рис. 43).
(рис. 43).
Направленный угол между вектором

и вектором

обозначается так:
 .
.
На чертеже направленный угол между векторами  и
и  показывают дугой со стрелкой, идущей от первого вектора ко второму.
показывают дугой со стрелкой, идущей от первого вектора ко второму.
Из определения направленного угла между векторами  и
и  следует, что он находится в следующих пределах:
следует, что он находится в следующих пределах:
 . .
|
Рассмотрим две прямоугольные декартовы системы координат 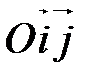 и
и 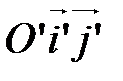 . Пусть М(х;у) в
. Пусть М(х;у) в 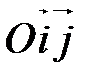 ,
,  в
в 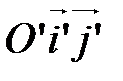 . Так как прямоугольная система координат - частный случай аффинной, то можно пользоваться формулами (5) из §12, но коэффициенты
. Так как прямоугольная система координат - частный случай аффинной, то можно пользоваться формулами (5) из §12, но коэффициенты 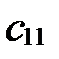 ,
,  ,
,  ,
,  уже не могут быть произвольными.
уже не могут быть произвольными.
Найдем координаты векторов  ,
,  в старой системе
в старой системе 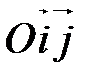 . Рассмотрим два случая.
. Рассмотрим два случая.
1) Базисы  ,
,  и
и  ,
,  одинаково ориентированы (рис. 44).
одинаково ориентированы (рис. 44).
Пусть направленный угол  . Приведем векторы
. Приведем векторы  и
и  к общему началу О (рис. 45).
к общему началу О (рис. 45).
Прямоугольные треугольники 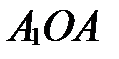 и
и 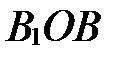 равны по гипотенузе и острому углу (
равны по гипотенузе и острому углу ( ,
,  ), следовательно,
), следовательно,  и
и  .
.
Из  находим:
находим:
 ;
;
 .
.
Следовательно, 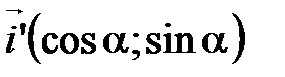 .
.
 ;
; 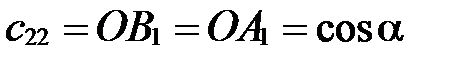 .
.
Следовательно,  . Тогда формулы (5) примут вид:
. Тогда формулы (5) примут вид:
 ;
;
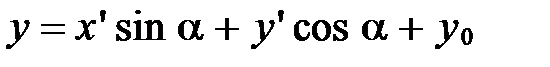 . (8)
. (8)
Заметим, что определитель матрицы перехода от базиса  ,
,  к базису
к базису  ,
, 
 .
.
2) Базисы  ,
,  и
и  ,
,  противоположно ориентированы (рис. 46).
противоположно ориентированы (рис. 46).
Пусть

. Приведем векторы

и

к общему началу
О (рис. 47).
Рассуждая аналогично случаю 1), получим:
 ;
;
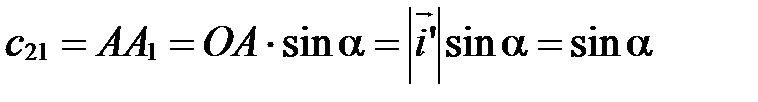 ;
;
 ;
; 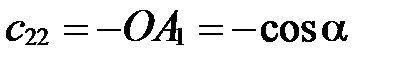 .
.
Следовательно,  ;
;  .
.
Тогда формулы (5) примут вид:
 ;
;
 . (9)
. (9)
Заметим, что определитель матрицы перехода от базиса  ,
,  к базису
к базису  ,
,  в этом случае
в этом случае
 .
.
Формулы (8) и (9) можно объединить:
 .
.
Частные случаи преобразования
Прямоугольной системы координат
1. Перенос начала:  ,
,  .
.
 . .
|
2. Поворот координатных векторов на угол a:  ,
,  .
.
Задания для самостоятельной работы
1. Определите (приближенно), чему равна величина направленного угла  (рис. 48, а, б).
(рис. 48, а, б).
2. Может ли величина направленного угла между векторами быть равна  ?
?  ?
?  ? Почему?
? Почему?
3. Найдите формулы преобразования прямоугольной системы координат, если координатные векторы повернуты на угол  , а начало координат перенесено в точку
, а начало координат перенесено в точку  .
.
4. Как по формулам преобразования координат узнать, какая система координат подвергается преобразованию: аффинная или прямоугольная?
5. Сделайте чертежи старой и новой систем координат для частных случаев преобразования прямоугольной декартовой системы координат.
Полярные координаты
Если указано правило, по которому положение точек плоскости можно определить с помощью упорядоченных пар действительных чисел, то говорят, что на плоскости задана система координат. Кроме аффинной системы координат, которая была рассмотрена в §10, в математике часто применяют полярную систему координат на плоскости.
Система полярных координат вводится на ориентированной плоскости.
Пара, состоящая из точки О и единичного вектора  , называется полярной системой координат и обозначается
, называется полярной системой координат и обозначается  или
или  . Направленная прямая
. Направленная прямая  называется полярной осью, точка О - полюсом (рис. 49).
называется полярной осью, точка О - полюсом (рис. 49).
Пусть
М – произвольная точка плоскости. Расстояние

от точки
О до точки
М называется
полярным радиусом точки М.
 . .
|
Таким образом,  . Если М совпадает с О, то
. Если М совпадает с О, то 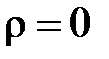 . Для любой точки М ее полярный радиус
. Для любой точки М ее полярный радиус
Направленный угол

называется
полярным углом точки М (рис. 50).
 . .
|
Если М совпадает с полюсом О, то j - неопределенный. Из определения направленного угла между векторами (см. §13) следует, что полярный угол
Полярный радиус r и полярный угол j называются полярными координатами точки
М.
На рис. 51 построены точки 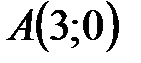 ,
,  ,
,  по их полярным координатам.
по их полярным координатам.
Выведем формулы перехода от полярных координат к прямоугольным декартовым и обратно.
Пусть  - полярная система координат на ориентированной плоскости,
- полярная система координат на ориентированной плоскости,  ,
,  в
в  . Присоединим к полярной системе
. Присоединим к полярной системе  единичный вектор
единичный вектор  , ортогональный вектору
, ортогональный вектору  так, чтобы базис
так, чтобы базис  ,
,  был правым (рис. 52).
был правым (рис. 52).
 ,
, 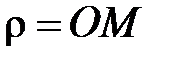 .
.
Пусть М(х;у) в  . Тогда
. Тогда  ;
;  (рис. 52).
(рис. 52).
Получили формулы перехода от полярных координат к прямоугольным:
Возведем обе части этих равенств в квадрат и сложим:
 , откуда
, откуда 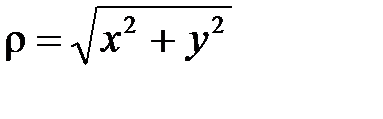 (корень берется со знаком «+», т.к.
(корень берется со знаком «+», т.к.  ).
).  Þ
Þ  Þ
Þ 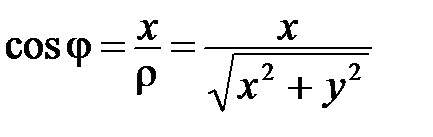 ;
; 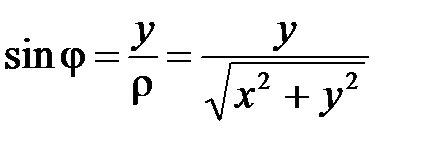 .
.
Получили формулы перехода от прямоугольных декартовых координат к полярным:
Замечание. При решении задач на переход от прямоугольных декартовых координат к полярным недостаточно найти только

или только
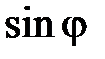
, т.к. по одной тригонометрической функции определить полярный угол однозначно невозможно: в промежутке

существуют два угла с одинаковыми косинусами (два угла с одинаковыми синусами) (рис. 53). Поэтому правильно найти полярный угол j вы сможете, только если одновременно вычислите

и
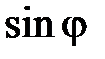
.
Воспользуйтесь поиском по сайту:


 и
и  - ненулевые векторы, заданные в определенном порядке (
- ненулевые векторы, заданные в определенном порядке ( - первый вектор,
- первый вектор,  - второй вектор).
- второй вектор). ||
||  , то направленным углом между вектором
, то направленным углом между вектором  и вектором
и вектором  называется
называется , если базис
, если базис  ,
,  - правый;
- правый; , если базис
, если базис  ,
,  - левый.
- левый. , то направленный угол между ними считается равным
, то направленный угол между ними считается равным  , если
, если  , то
, то  (рис. 43).
(рис. 43).











 и вектором
и вектором  обозначается так:
обозначается так:
 .
. и
и  показывают дугой со стрелкой, идущей от первого вектора ко второму.
показывают дугой со стрелкой, идущей от первого вектора ко второму. и
и  следует, что он находится в следующих пределах:
следует, что он находится в следующих пределах: .
.
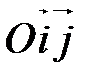 и
и 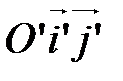 . Пусть М(х;у) в
. Пусть М(х;у) в 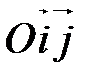 ,
,  в
в 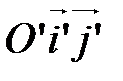 . Так как прямоугольная система координат - частный случай аффинной, то можно пользоваться формулами (5) из §12, но коэффициенты
. Так как прямоугольная система координат - частный случай аффинной, то можно пользоваться формулами (5) из §12, но коэффициенты 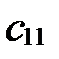 ,
,  ,
,  ,
,  уже не могут быть произвольными.
уже не могут быть произвольными. ,
,  в старой системе
в старой системе 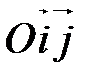 . Рассмотрим два случая.
. Рассмотрим два случая. ,
,  и
и  ,
,  одинаково ориентированы (рис. 44).
одинаково ориентированы (рис. 44).



 . Приведем векторы
. Приведем векторы  и
и  к общему началу О (рис. 45).
к общему началу О (рис. 45).

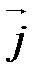



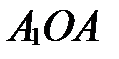 и
и 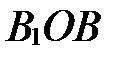 равны по гипотенузе и острому углу (
равны по гипотенузе и острому углу ( ,
,  ), следовательно,
), следовательно,  и
и  .
. находим:
находим: ;
; .
.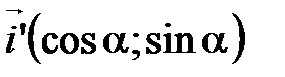 .
. ;
; 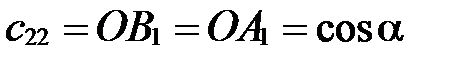 .
. . Тогда формулы (5) примут вид:
. Тогда формулы (5) примут вид: ;
;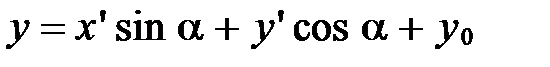 . (8)
. (8) ,
,  к базису
к базису  ,
, 
 .
. ,
,  и
и  ,
,  противоположно ориентированы (рис. 46).
противоположно ориентированы (рис. 46).









 . Приведем векторы
. Приведем векторы  и
и  к общему началу О (рис. 47).
к общему началу О (рис. 47).
 ;
;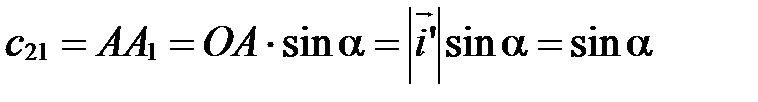 ;
; ;
; 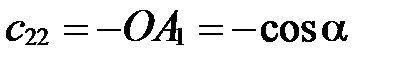 .
. ;
;  .
. ;
; . (9)
. (9) ,
,  к базису
к базису  ,
,  в этом случае
в этом случае .
. ,
,
 ,
,

 .
. ,
,  .
. .
.
 ,
,  .
.
 (рис. 48, а, б).
(рис. 48, а, б).



 ?
?  ?
?  ? Почему?
? Почему? , а начало координат перенесено в точку
, а начало координат перенесено в точку  .
. , называется полярной системой координат и обозначается
, называется полярной системой координат и обозначается  или
или  . Направленная прямая
. Направленная прямая  называется полярной осью, точка О - полюсом (рис. 49).
называется полярной осью, точка О - полюсом (рис. 49).
 от точки О до точки М называется полярным радиусом точки М.
от точки О до точки М называется полярным радиусом точки М.
 .
.
 . Если М совпадает с О, то
. Если М совпадает с О, то 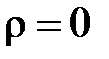 . Для любой точки М ее полярный радиус
. Для любой точки М ее полярный радиус
 называется полярным углом точки М (рис. 50).
называется полярным углом точки М (рис. 50).
 .
.

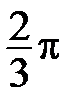

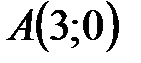 ,
,  ,
,  по их полярным координатам.
по их полярным координатам.

 - полярная система координат на ориентированной плоскости,
- полярная система координат на ориентированной плоскости,  ,
,  в
в  . Присоединим к полярной системе
. Присоединим к полярной системе  единичный вектор
единичный вектор  , ортогональный вектору
, ортогональный вектору  так, чтобы базис
так, чтобы базис  ,
,  был правым (рис. 52).
был правым (рис. 52). ,
, 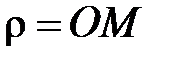 .
. . Тогда
. Тогда  ;
;  (рис. 52).
(рис. 52).
 , откуда
, откуда 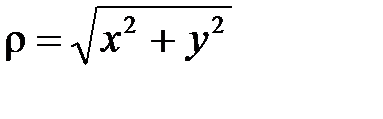 (корень берется со знаком «+», т.к.
(корень берется со знаком «+», т.к.  ).
).  Þ
Þ  Þ
Þ 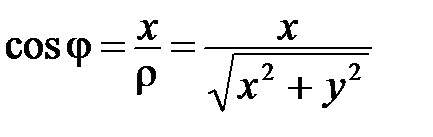 ;
; 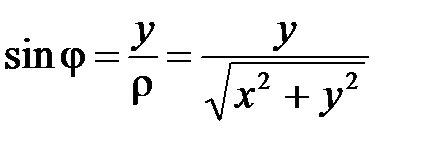 .
.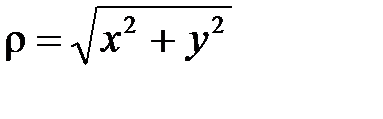 ,
,
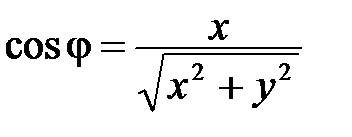 ,
,
 .
.


 или только
или только 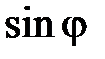 , т.к. по одной тригонометрической функции определить полярный угол однозначно невозможно: в промежутке
, т.к. по одной тригонометрической функции определить полярный угол однозначно невозможно: в промежутке  существуют два угла с одинаковыми косинусами (два угла с одинаковыми синусами) (рис. 53). Поэтому правильно найти полярный угол j вы сможете, только если одновременно вычислите
существуют два угла с одинаковыми косинусами (два угла с одинаковыми синусами) (рис. 53). Поэтому правильно найти полярный угол j вы сможете, только если одновременно вычислите  и
и 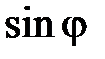 .
.


