Иллюстрация применения процедуры многомерного выбора

При решении некоторой конкретной производственной задачи используется шесть показателей: полная себестоимость реализованной товарной продукции (e₁), удельная прибыль (e₂), материалоемкость (e₃), фондоотдача (e₄), обеспеченность рабочей силой (e₅), ритмичность выпуска (e₆).

Эти показатели получили оценки 19 специалистов по 10-балльной шкале. Экспертные оценки показателей представлены в таблице 17.

Таблица 17

Оценки показателей каждым из опрошенных экспертов

Эксперт Критерий	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
e1	1	9	5	10	7	10	5	10	5	3	8	5	3	8	6	10	10	6	7
e2	3	4	5	8	5	3	8	5	8	7	2	8	8	6	5	9	9	3	3
e3	8	3	2	5	5	5	8	5	4	2	1	2	7	7	10	8	6	3	10
e4	2	6	2	5	10	5	10	10	9	6	3	1	2	6	2	2	4	5	5
e5	10	10	4	8	8	10	10	10	4	5	6	8	7	10	8	8	10	8	7
e6	9	8	3	5	5	4	10	8	6	7	10	10	9	10	7	3	5	6	6

Задача состоит в выборе наиболее значимого показателя (или группы показателей) при разных предположениях относительно требований к точности совпадения мнений всех экспертов.

Таким образом, в рассматриваемом примере в качестве объектов выступают перечисленные шесть показателей Е = {e_i}, i = 1…6, которые необходимо упорядочить с учетом мнений K экспертов, k = 1, 2…19.

Эксперты имеют одинаковую квалификацию и можно положить коэффициенты относительной значимости π_k равными между собой и равными «1».

Множество возможных результатов P_k, k = 1, 2…19 упорядочены по десятибалльной шкале с шагом, равным единице и одинаковы для всех k. Оценки рассматриваемых показателей каждым из опрашиваемых экспертов α^k_i, i = 1…6, k = 1…19 совпадают с данными таблицы 17.

Определим для каждой пары объектов (e_i, e_j) коэффициенты соответствия c_ij предположению, что объект e_i предпочтительнее объекта e_j. Результаты представляются в виде следующей матрицы:

	ei ej	e1	e2	e3	e4	e5	e6
С =	e1	х	0,37	0,26	0,37	0,74	0,53
	e2	0,68	х	0,47	0,53	0,74	0,74
	e3	0,74	0,74	х	0,58	0,89	0,74
	e4	0,74	0,54	0,58	х	0,84	0,74
	e5	0,47	0,37	0,26	0,26	х	0,37
	e6	0,47	0,31	0,31	0,26	0,74	х

Предположим, что e₁ предпочтительнее e₂. Это предположение разделяют 13 экспертов. Множество критериев, соответствующих этому предположению

С₁₂ ={2,3,4,5,6,8,11,14,15,16,17,18,19}.

Так как коэффициенты значимости π_k = 1, то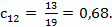

Множество критериев, соответствующих предположению e₂ предпочтительнее e₁

С₂₁ ={1,3,7,9,10,12,13} и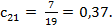

Значения показателей несоответствия для всех пар (e_i, e_j) могут быть представлены в виде матрицы Д (s). Полагая s =1, получим:

 

	ei ej	e1	e2	e3	e4	e5	e6
Д (1) =	e1	х	0,7	0,7	0,8	0,2	0,7
	e2	0,5	х	0,6	0,7	0,4	0,6
	e3	0,7	0,7	х	0,8	0,3	0,5
	e4	0,5	0,5	0,5	х	0,5	0,5
	e5	0,9	0,7	0,7	0,8	х	0,6
	e6	0,8	0,8	0,9	0,9	0,4	х

Для s = 2

	ei ej	e1	e2	e3	e4	e5	e6
Д (2) =	e1	х	0,6	0,6	0,6	0,2	0,6
	e2	0,4	х	0,5	0,7	0,2	0,3
	e3	0,4	0,5	х	0,6	0,3	0,4
	e4	0,4	0,5	0,5	х	0,2	0,3
	e5	0,5	0,7	0,6	0,7	х	0,5
	e6	0,6	0,6	0,8	0,7	0,3	х

Так, для пары (e₁, e₂) показатель d₁₂ (1) рассчитывается следующим образом:

(1) Выделяется множество Д₁₂ экспертов, не согласных с предложением предпочтительности объекта e₁ по отношению к e₂.

Д₁₂ = {1,7,9,10,12,13}.

(2) Для каждого kϵД₁₂ определяется величина несоответствия: [α^k₂ - α^k₁] – {2,3,3,4,3,5}.

(3) Величины, полученные в (2), упорядочиваются в невозрастающую последовательность – {5,4,3,3,3,2}.

(4) Показатель несоответствия d₁₂ (1) = 5/10 = 0,5 – вычисляется как отношение первого члена последовательности (3) к высоте самой большой шкалы. В нашем примере она равна 10. Соответственно, при s = 2 d₁₂ (2) = 4/10 = 0,4 и т.д.

Данные матриц С и Д (s) позволяют построить графы сравнения объектов при различных требованиях к порогам соответствия и несоответствия и выделить множество объектов E’, составляющих ядро соответствующего графа (см. рис. 1). Объекты, входящие в ядро графа, отмечены кружками.

 

 

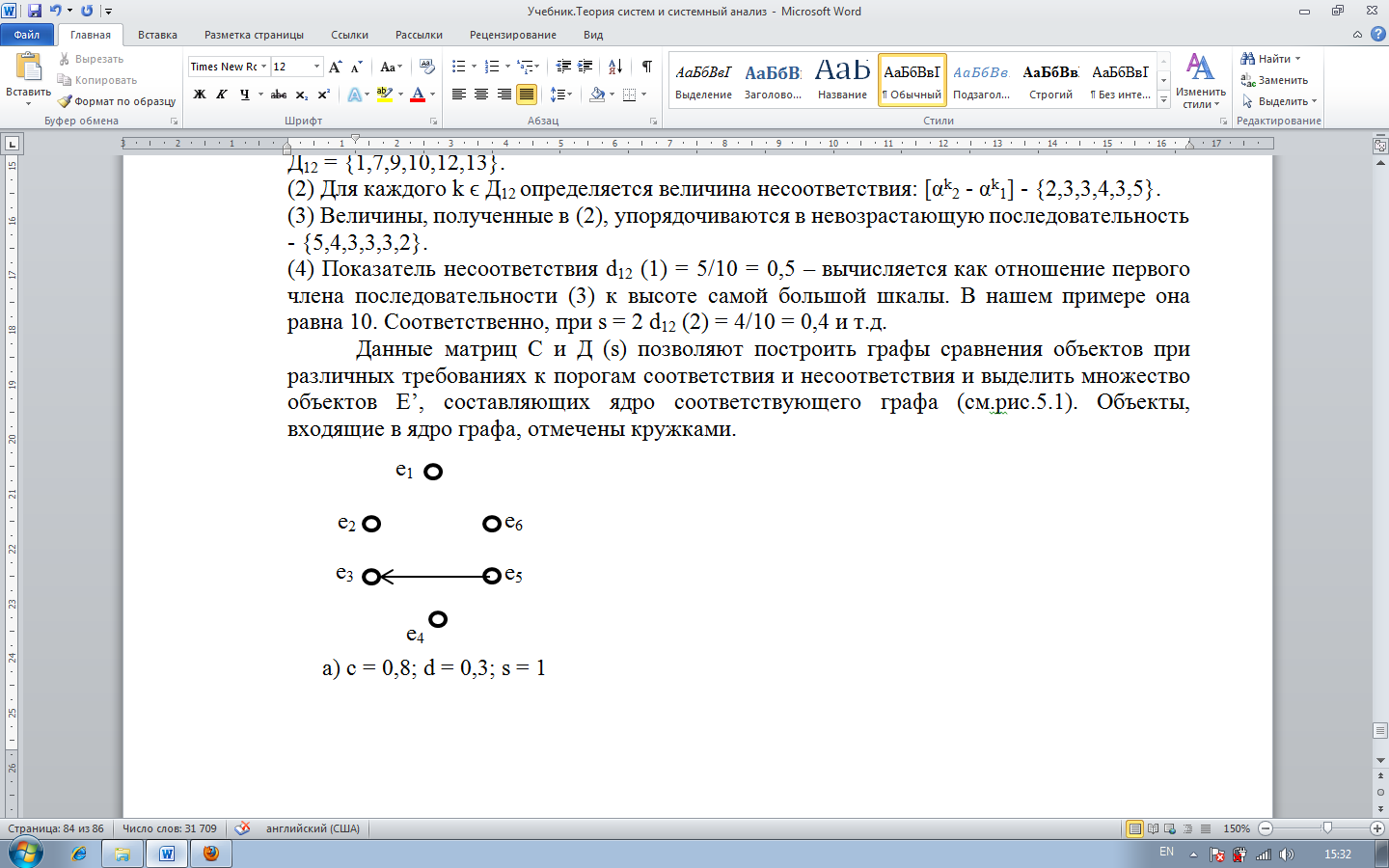
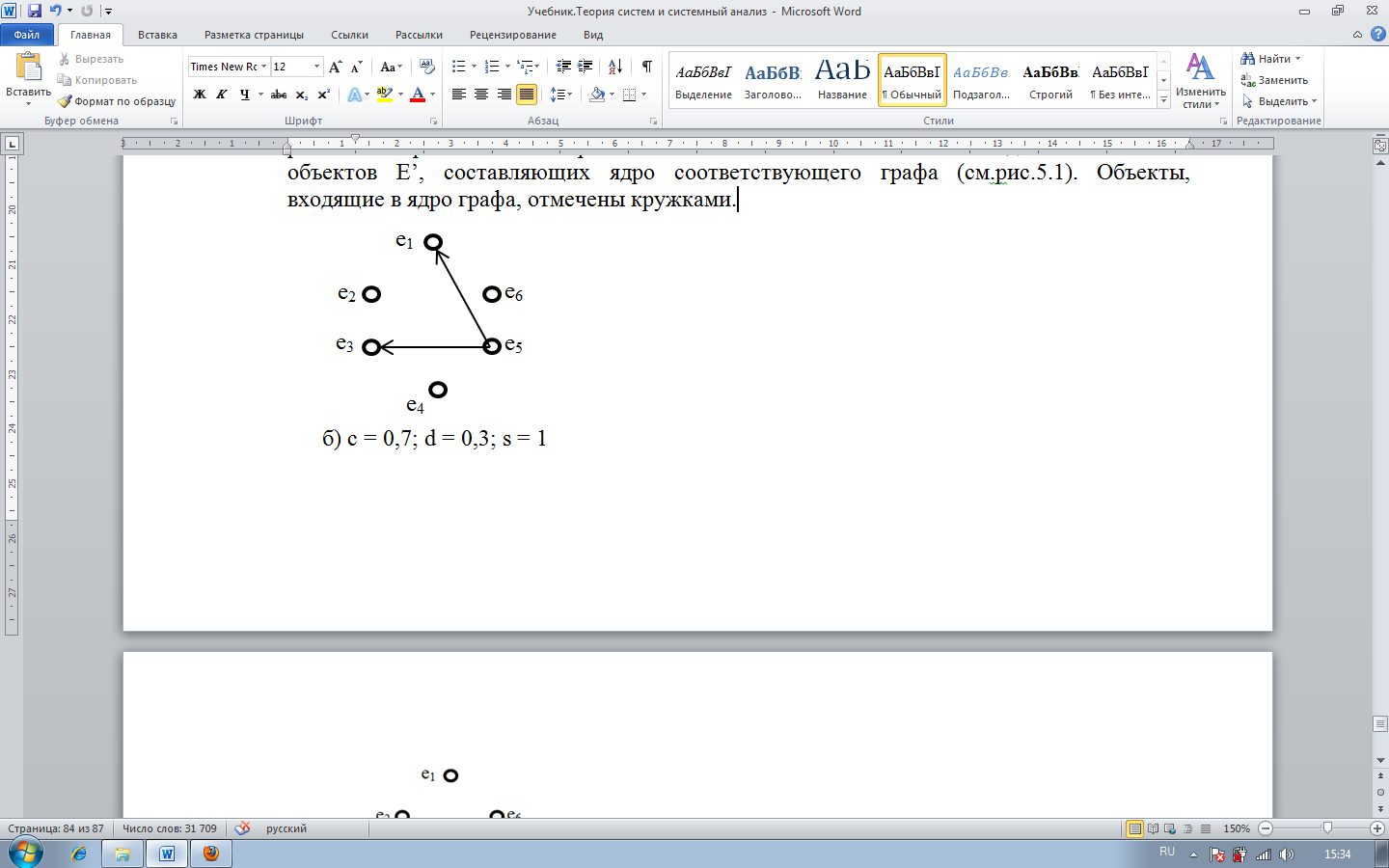
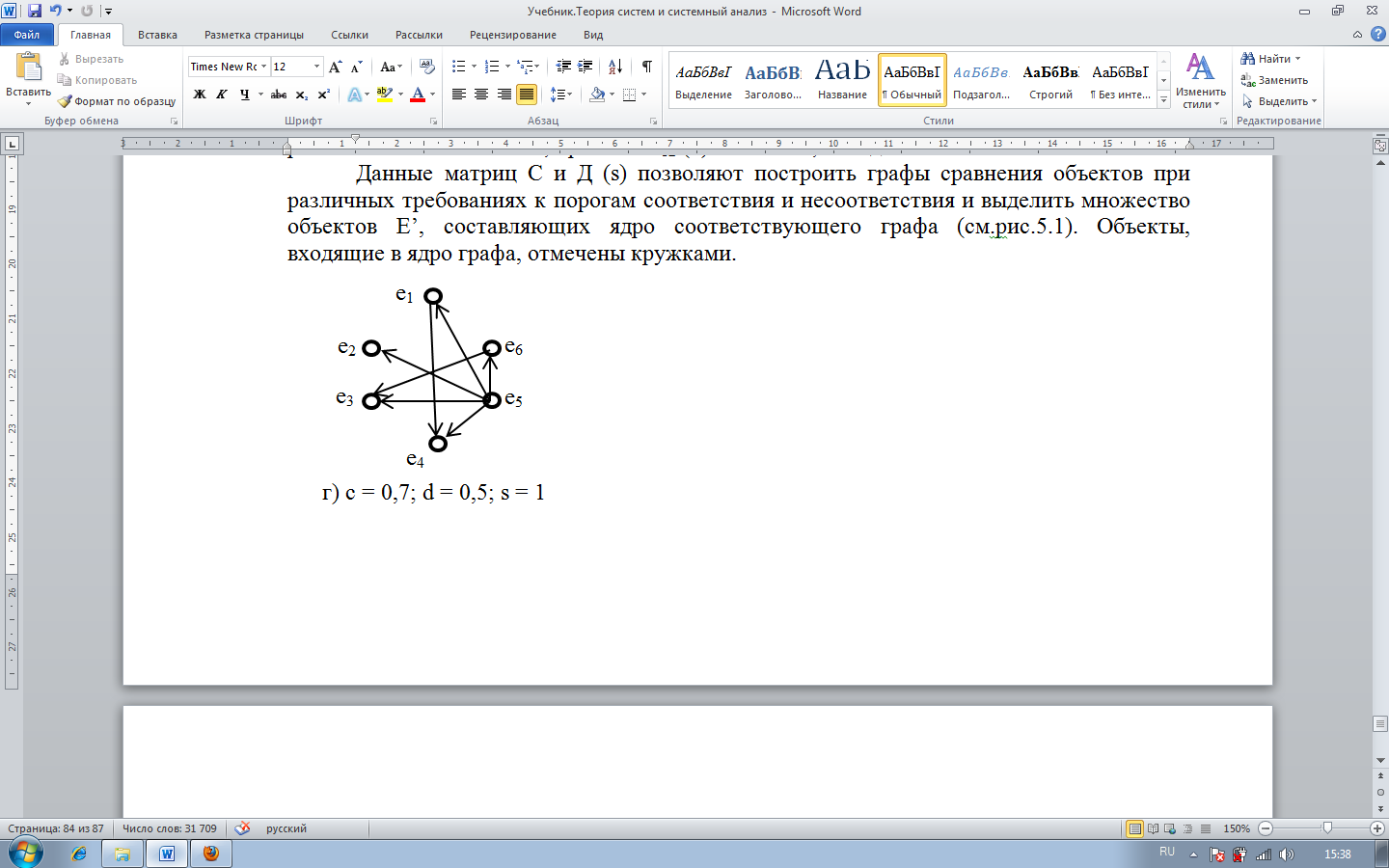
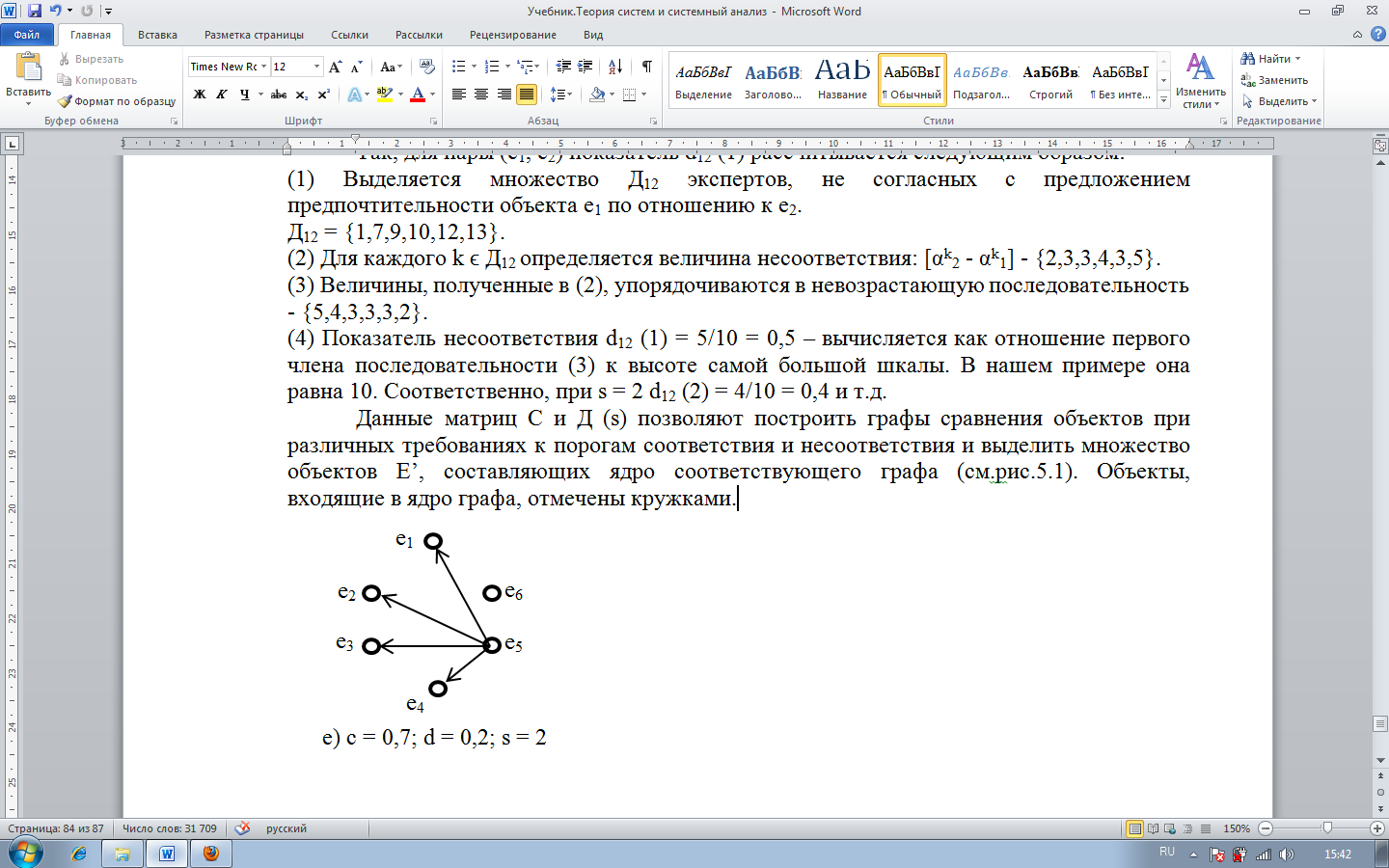
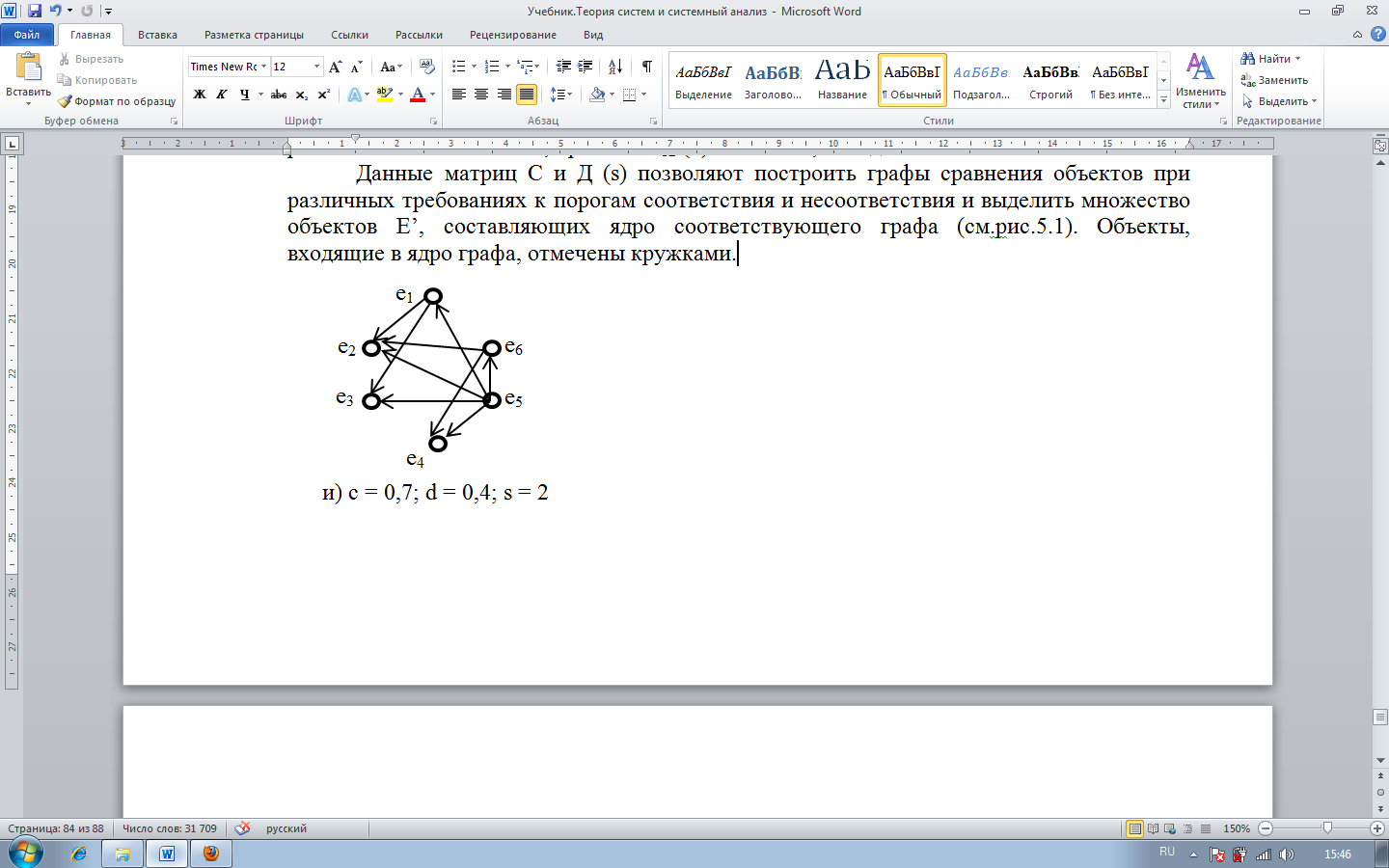
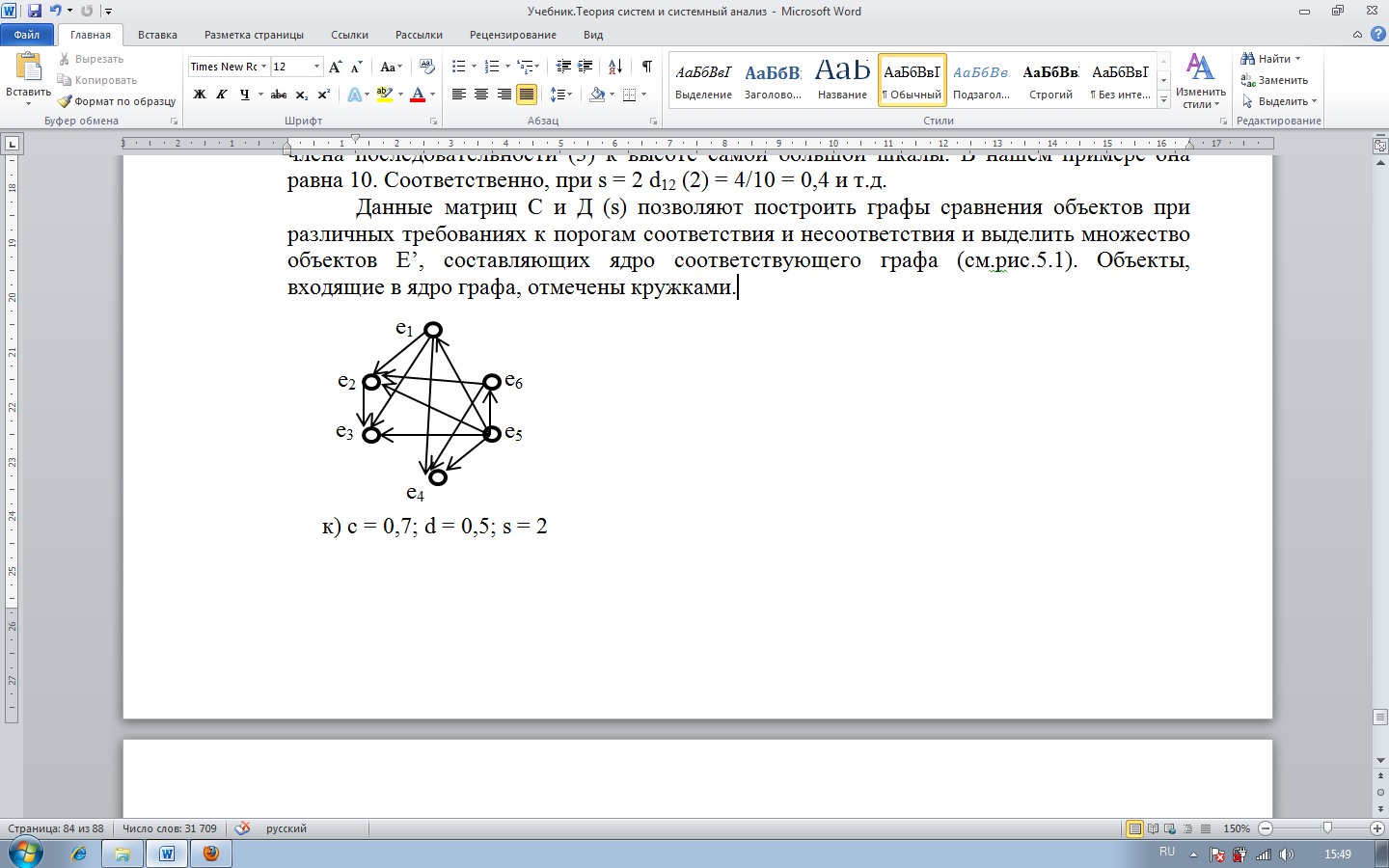
Рис. 1. Сравнение объектов при различных требованиях к параметрам согласования выбора

Рассмотрим «эволюцию» ядер графов. Полагая s = 1 и принимая пороги соответствия к несоответствия равными С = 0,8, d = 0,3, возможно провести сравнение только для двух элементов (показателей) e₃ и e₅ (рис. 1-а). Ядро графа G (0,8; 0,3; 1) включает в себя пять элементов – {e₁, e₂, e₄, e₅, e₆}. Другими словами, эти показатели при указанных требованиях к совпадению мнений экспертов не сравнимы между собой. При этом показатель e₅ – (обеспеченность рабочей силой) признается более значимым, чем показатель материалоемкости e₃.

Снижение требований к порогу соответствия С = 0,7 приводит к дополнительной возможности сравнения показателей e₁ и e₅ (рис. 1-б). Следовательно, ядро графа G (0,7; 0,3; 1) содержит теперь элементы {e₂, e₄, e₅, e₆}.

При s = 2 и тех же порогах соответствия ядро графа G (0,7; 0,3; 2) содержит единственный элемент (показатель), превосходящий все остальные (рис. 1-ж). Таким образом, показатель e₅ – обеспеченность рабочей силой – может быть принят в качестве основного при решении данной проблемы с указанной степенью риска, отраженной набором оценок степени согласованности мнений экспертов. Отметим, что дополнительной информацией, которая может оказаться полезной при принятии решений является то, что ритмичность производства (e₆) в данных условиях требует больше внимания руководства, чем показатель фондоотдачи (e₄). Точно также введение более строгих требований к порогу несоответствия (уменьшение значения d с 0,3 до 0,2) приводит к введению в ядро графа элемента e₆ (рис. 1-е). При таких ограничениях сравнение между показателями e₅ и e₆провести не представляется возможным без дополнительных исследований. Аналогично, анализируется все другие графы и их ядра.

Отметим, что упорядочивание по так называемым «взвешенным суммам» – 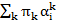 – приводит к следующим результатам:

 

Показатели	e5	e6	e1	e2	e3	e4
Взвешенные суммы	151	134	127	108	101	95

 

На основе этого метода показатель e₅ становится самым значимым, что совпадает с результатом, полученным при использовании описанной выше процедуры. Однако метод «взвешенных сумм» не позволяет сделать вывод о том, что мнения экспертов наиболее противоречивы относительно показателей е₆ и е₁. Таким образом, показатель e₆ не может автоматически быть принят как основа для выбора в том случае, если по каким-либо причинам показатель е₅ не принимается во внимание. Необходимо углубить сравнение е₆ и е₁ для более обоснованного выбора.

Интересно отметить, что только анализ ядер представленных графов позволяет выявить противоречивость мнений о показателе е₄. В то время как метод «взвешенных сумм» присваивает этому показателю минимальную оценку и тем самым не включает его в сферу первостепенного внимания лиц, ответственных за принятие решений, приоритет е₅ над е₄ проявляется при «несильных» требованиях к согласованности мнений экспертов. Дуга (е₅, е₄) появляется лишь в графе G (0,7; 0,5; 1) (рис. 1-г).

Исследование изменений ядер графов в зависимости от изменения требований к параметрам согласования различных критериев (в данном случае различных мнений экспертов) позволяет упорядочить рассматриваемые объекты или их группы по предпочтительности для каждых заданных значений параметров с и d (s). Значения параметров с и d (s) являются как бы оценками риска в принятии решения. Так при довольно высоких требованиях к значениям с и d (s) (см. рис. 1-а) G (0,8; 0,2; 1) все рассматриваемые объекты можно разделить лишь на две подгруппы {е₁, е₂, е₄, е₅, е₆}, {е₃}. Объекты, составляющие первую подгруппу, неразделимы при заданных требованиях точности. Уменьшение требований к значениям с и d, до 0,7 и 0,3, соответственно позволяет получить более детальное разделение {е₅}, {е₁, е₂, е₆}, {е₄, е₃}. Ранжирование объектов же, соответствующее упорядочиванию по методу средней арифметической, характеризуется довольно плохой согласованностью мнений экспертов (с = 0,7; d (1) = 0,5). Решение, полученное по методу средних, может, таким образом, получить количественную оценку степени его обоснованности. Такая количественная оценка может быть поставлена в соответствие и любому другому решению.

Предыдущая23242526272829303132333435363738Следующая

Поделиться:

Воспользуйтесь поиском по сайту: