 |
Слово, информация, алгоритм.
|
|
|
|
Лекция 1.
Часть I. Введение.
Тематика курса.
Очень упрощенно тематику курса можно представить в виде такой схемы.
Дано множество W (множество элементов, множество объектов, множество слов и т.п.; упорядоченное множество, пространство, метрическое пространство и т.п.). Задано свойство S, которым обладает часть элементов этого множества Ws. Требуется найти значения |Ws|, оценки значения |Ws|, оценки, значение или асимптотику отношения |Ws||/|W|и т.п.
Вы скажете, что это чисто комбинаторная задача, и в предыдущих курсах по дискретному анализу (а также в других) вы только этим и занимались. На это есть два возражения: конструктивное и неконструктивное.
Неконструктивное. Название нашего курса содержит слова «Дополнительные главы …». Это значит, что мы будем брать темы, до которых в предыдущих курсах руки не дошли.
Конструктивное. Обозначим некоторые особенности, акценты, выделяющие тематику курса. Такие особенности в предыдущих и текущих курсах дискретного анализа задавались, например, следующими понятиями: булевы функции, алгебра логики, алгебраические конструкции (высшая алгебра), теория алгоритмов, формальные системы, комбинаторные методы и пр.
Ключевым объектом исследования у нас будет понятие «слово». Понятие слово тесно связано с понятием информация, а понятие информация – с понятием алгоритм.
Понять, что такое «информация», пока не удалось никому. Однако многочисленные исследования и рассуждения на тему этого феномена позволяют предположить, что тут есть определённая проблема, находящаяся на стыке математики и других естественных и гуманитарных дисциплин.
Принято считать, что информация «локализует» объект и что чем больше информации об объекте, тем точнее его можно определить.
|
|
|
Не менее трудно понять, что такое «передача информации», если не ограничиваться классической моделью Шеннона и попытаться найти адекватные выражения и описания для значительно более общих ситуаций. В частности, передача информации и перенос информации могут означать разные деяния.
Причинно-следственные связи являются важнейшим компонентом любой науки, но не имеют сколько-нибудь серьёзного фундамента за пределами ряда разделов точных наук.
Одним из способов выражения такого рода связей является понятие «зависимости». Такая зависимость может быть «функциональной», «линейной», «вероятностной» и так далее.
Понятие информации даёт возможность ввести в обиход «информационную» зависимость, выражающую в какой-то степени один из видов причинно-следственных связей, но не совпадающих ни с одним из приведённых выше видов зависимостей.
Под анализом информации обычно подразумевают извлечение полезных данных из «текста», в котором эти данные представлены косвенным, искажённым или недостаточно полным образом. Такой анализ необходим во многих содержательных ситуациях, связанных с восстановлением повреждённых сообщений, сравнением генетических последовательностей, автоматическим переводом с одного языка на другой и так далее.
Ключевые понятия в такой деятельности следующие: текст, контекст, слово, фрагмент, подслово, смысл, форма, содержание, близость, похожесть и так далее.
Под анализом понимается изучение изучение возможностей восстановления исходной информации с максимальной достоверностью.
Исходным объектом является слово. Это слово представимо некоторым набором своих частей. Требуется путём анализа этих частей восстановить исходное слово с той точностью, которую допускает исходная информация. Под «точностью» в содержательном смысле понимается множество всех кандидатов на роль неизвестного слова. Под контекстом понимается априорная информация или информация о множестве слов, которому заведомо принадлежит предмет поиска. Априорная информация может иметь различную форму: предикатное описание, «таблица обучения», набор признаков, геометрическое расположение и так далее.
|
|
|
Например, объекты из упомянутого выше множества W надо как-то задавать, кодировать. Здесь возникают слова как коды объектов. Значения и оценки |Ws|, упомянутые выше, надо как-то получать. Один из самых распространенных приемов – сконструировать процедуру порождения объектов из Ws и посмотреть, сколько объектов она породит. Здесь и возникает алгоритм.
Слово, информация, алгоритм.
Два интуитивных понятия: информация и алгоритм взаимно обуславливают друг друга.
Формальные подходы к понятию алгоритма заслужили внимание благодаря гипотезам типа тезиса Черча.
Этот тезис говорит об эквивалентности широкого неформального и смутного понятия "интуитивный алгоритм" узкому и весьма замысловатому, на первый взгляд, формализму типа алгорифма Маркова или машины Тьюринга (МТ). Утверждается, что для любой задачи, для которой существует «интуитивный» алгоритм решения, можно, например, построить МТ, которая будет решать эту задачу.
Сделаем одно замечание. Во всех перечисленных ниже формальных подходах алгоритм имеет дело с преобразованием одних слов в другие. То есть, условие задачи Z, которую решает алгоритм, можно рассматривать как слово в некотором алфавите A.
Обозначим все множество слов этого алфавита через A*. Подмножество слов алфавита назовем языком. Обратим внимание, что в содержательном смысле не все слова алфавита являются условиями индивидуальных задач из Z.
Очевидно, что алгоритма без информации не существует. Если мы хотим дать определение алгоритма, нам нужно определение информации.
Следующая фраза, конечно, не является математическим определением (а такового, видимо, и не существует для «интуитивно очевидных понятий» типа информации, числа, алгоритма и пр.), но кое-что проясняет.
Информация – это продукт деятельности субъекта (человека), предназначенный для другого субъекта (человека), представляющий собой инструкцию (часть инструкции) по преобразованию окружающего мира с минимальными затратами ресурсов (энергии).
|
|
|
Но, как и для алгоритма, для информации существует тезис, в каком-то смысле «заменяющий» определение.
Тезис. Любая информация может быть представлена словом в конечном алфавите.
Справедливо и обратное: информации без алгоритма не существует.
По поводу этих тезисов заметим, что они справедливы только в одну сторону. Не любая Машина Тьюринга представляет собой алгоритм и не любое слово является информацией!
Итак, условие задачи – это информация, текст алгоритма – информация, результат работы алгоритма – информация и т.п. Еще раз хочу подчеркнуть, что нет алгоритма без информации и наоборот.
Теперь поясним, что будет пониматься под количеством информации, кодированием информации и сжатием информации.
Очевидно, что множество слов может быть представлено одним словом. (Например, с помощью операции конкатенации.)
Опр. Количество символов в слове α будем называть длиной слова α и обозначать через l(α) или |α|.
Опр. Конкатенация слов  и
и  получается путем последовательной записи символов одного слова вслед за символами другого, т.е.
получается путем последовательной записи символов одного слова вслед за символами другого, т.е.

Поэтому понятия кодирование информации, количества информации и сжатие информации могут относиться как к одному слову, так и к множеству слов.
Кодирование информации – это создание слова α в алфавите А.
Так как информация словом не является, а лишь представляется, а не любое слово – это информация, то слово, представляющее собой информацию (об объекте) будем называть информационным объектом.
Количество информации – это некоторая количественная характеристика H(α), сопоставляемая слову (множеству слов) α.
Сжатие информации - это преобразование одного слова α в другое слово β. Поэтому сжатие – это преобразование информации, которое можно задать с помощью некоторого отображения φ. Таким образом, β=φ(α).
Вообще говоря, термин сжатие информации тесно связан с понятием количества информации. Сжатие происходит тогда, когда количество информации, приходящейся на один символ исходного слова α меньше, чем количество информации, приходящейся на один символ слова β=φ(α).
|
|
|
Понятие кодирование применительно к информации будет рассматриваться в двух аспектах:
Создание самого Информационного объекта. То есть нанесение на материальный носитель информации о некотором объекте в виде слова α в алфавите А. В этом случае данное слово будет рассматриваться как код объекта. То есть код объекта – это символ интерпретации субъектом информации об объекте. (Назовем это кодированием в широком аспекте.)
Преобразование информации. Вначале информация была представлена словом α, а затем эта же информация представляется словом β, которое получено из α в результате некоторого преобразования φ. Тогда слово β=φ(α) называется кодом слова α. (Назовем это просто кодированием.)
| Преобразование одних слов в другие слова. |
| Код. Кодирование. |
| Код объекта – символ интерпретации субъектом информации об объекте. |
Первый аспект возникает тогда, например, в программировании, когда нужно представить объект в виде набора данных. Эта проблема возникает как для «математических объектов»: числа, фигуры, группы, поля, алгоритмы и т.п., так и для объектов из других областей знаний: месторождения в геологии, болезни в медицине, каталоги в промышленности и т.п. Здесь результатом кодирования является слово, в то время как исходный объект кодирования либо представляет собой формализованный математический объект, либо вообще не формализован.
Часто бывает, что кодирование (создание информационного объекта) - это итерационный процесс. То есть, сначала есть объект B, есть информация о нём I(B), потом есть информация об информации о нём I(I(B)) и т.д. В результате можно получить некоторую структуру данных, состоящую из всех таких информаций.

Примеры кодировок
Приведем простые примеры кодирования объектов.
Целые числа
Целое число n может быть представлено (закодировано), например, следующими тремя способами.
а) Словом α = 01…10 (n штук «1» и 0 по бокам) в алфавите А=(0,1). В этом случае длина кода l(α) (количество символов алфавита в слове) равна n +2;
б) Словом α = a 1 a 2 … ak в виде десятичной записи в алфавите А=(0,1,…,9). Длина кода равна [lg n ]+1.
в) В мультипликативной форме (произведение степеней простых множителей) в виде слова α = a 1 p 1 a 2 p 2 … akpk, (здесь a 1 … ak – простые числа).
Длина кода: 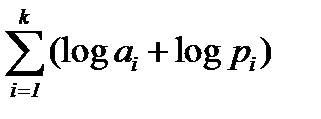 .
.
Вектора и матрицы
Вектор с компонентами a 1 … an, записанными в десятичной форме имеет, может быть представлен в виде слова длины lg n +  .
.
|
|
|
Матрица M с компонентами в десятичной форме, M=  , может быть представлена словом длины lg n + lg m +
, может быть представлена словом длины lg n + lg m +  .
.
G = ( V, E ) – неориентированный граф.
Здесь множество вершин обозначено через V, а множество ребер через E. Пусть | V | = n, | E | = m.
Граф можно представить, например, следующими тремя способами (все числа в десятичной форме)
а) Списком ребер {(i 1, j 1), (i 2, j 2), …, (im, jm)}.
б) Списком соседей (вершин), записанных последовательно для вершины 1, вершины 2,…, вершины n.

в) Матрицей смежности
A = | aij | n × n, 


 .
.
Алфавит А кроме арабских цифр будет включать вспомогательные разделители, например, «,» и «;».
Длина кода l(α) без учета разделителей для каждого из трех случаев следующая:
а) 4 n + 1 0 m ≤ l(α) ≤4 n + 1 0 m + (n + 2 n).
б) 2 n + 8 m ≤ l(α) ≤ 2 n + 8 m + 2log n.
в) l(α) = n 2 – n – 1.
Свойства кодировок
К коду β объекта α обычно применяют следующие требования.
Декодируемость. В случае кодирования (как преобразования слов) это свойство не вызывает вопросов. Пусть есть объект α, код β= φ(α). Декодируемость означает наличие возможности восстанавливать α по коду β= φ(α). В случае же кодирования в широком аспекте словом является только β. Сам объект α словом не является. Поэтому в каждом конкретном случае нужно определять понятие восстановление. В качестве примера можно привести пример присвоения идентификатора (слово в алфавите) неформализованному объекту (изделие, книга, человек). Здесь под восстановлением понимается нахождение конкретного объекта по его идентификатору.
Неизбыточность. Это требование означает стремление уменьшить длину кода. Но пока речь не идет об оптимизации и минимизации. Неизбыточность в широком смысле означает не поиск минимально возможной (по длине кода) кодировки, а использование кодировки без искусственного увеличения ее длины. То есть из слова-кода нельзя выбросить букву без нарушения требования дешифруемости.
Разумность. Это термин из теории сложности алгоритмов (см., например, [1], стр. 23-24). Он означает, что способ кодировки должен соответствовать тем целям, для которых информация будет использоваться в дальнейшем.
Например, если мы решаем задачу о простоте числа (по заданному натуральному числу N требуется ответить на вопрос, является ли это число простым), то кодировка в мультипликативной форме (см. пример выше) не является разумной. Для большинства практических задач первый из видов кодировок целого числа n в приведенном выше примере не является разумной кодировкой.
Пусть мы теперь имеем "разумные" кодировки. На этом уровне принимается интуитивная гипотеза о некоторой эквивалентности всех возможных "разумных" кодировок входных данных одной и той же массовой задачи.
Второй пример показывает варианты длины кодировок в зависимости от способа задания чисел. Варианты длины кодировок в третьем примере зависят уже от структуры входных данных. Но в обоих случаях можно говорить о, так называемой, полиномиальной эквивалентности.
В дальнейшем нам полезно будет понятие полиномиальной эквивалентности двух функций. Две неотрицательные функции S(n) и R(n) полиномиально эквивалентны, если существуют два полинома Q(x) и P(x) такие, что для всех n справедливы неравенства S(n)£P(R(n)) и R(n)£Q(S(n)).
Пусть S и R две "разумные" схемы кодирования задачи массовой Z. Длины входа в этих схемах для задачи I обозначим через S(I) и R(I). К ним можно применить определение полиномиальной эквивалентности.
В примере кодирования графа все три схемы полиномиально эквивалентны.
|
|
|


