 |
Отображения конечных множеств.
|
|
|
|
Если  ,
,  — конечные множества, то положим, по определению, что
— конечные множества, то положим, по определению, что  — это множество всех отображений из
— это множество всех отображений из  в
в  , то есть соответствий
, то есть соответствий  этого вида:
этого вида:

Каждое такое отображение может быть задано с помощью матрицы

где  ,
,  и
и  для
для  . Таким образом, первая строка матрицы
. Таким образом, первая строка матрицы  — это множество
— это множество  , а вторая — мультимножество над
, а вторая — мультимножество над  . Ясно, что число таких матриц
. Ясно, что число таких матриц  равно
равно  , и отсюда следует формула
, и отсюда следует формула

Если 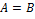 и
и  — взаимно однозначное отображение
— взаимно однозначное отображение  в себя, то
в себя, то  называется перестановкой и стандартная запись для
называется перестановкой и стандартная запись для  выглядит следующим образом:
выглядит следующим образом:

Множество 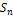 , где
, где  , называется множеством перестановок степени
, называется множеством перестановок степени  .
.
Как комбинаторный объект множество 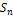 является неисчерпаемым источником проблем, зачастую имеющих глубокий математический и содержательный смысл.
является неисчерпаемым источником проблем, зачастую имеющих глубокий математический и содержательный смысл.
Если на множество 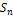 ввести операцию суперпозиции, то
ввести операцию суперпозиции, то 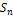 превращается в группу, которая называется симметрической группой степени
превращается в группу, которая называется симметрической группой степени  . Ясно, что
. Ясно, что  . Группа
. Группа 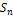 является универсальным алгебраическим объектом в силу следующего утверждения.
является универсальным алгебраическим объектом в силу следующего утверждения.
Теорема Кэли. Каждая конечная группа изоморфна некоторой подгруппе 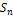 .
.
Каждая перестановка  единственным образом разлагается в произведение независимых циклов:
единственным образом разлагается в произведение независимых циклов:
 (1.4)
(1.4)
где  . Представление (1.4) играет существенную роль во многих проблемах, связанных с группой
. Представление (1.4) играет существенную роль во многих проблемах, связанных с группой 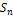 . Например, по разложению (1.4) легко найти порядок элемента g в группе
. Например, по разложению (1.4) легко найти порядок элемента g в группе 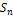 . Действительно, искомый порядок
. Действительно, искомый порядок  равен Н.О.К. длин циклов
равен Н.О.К. длин циклов 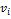 , то есть
, то есть
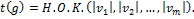
Упражнения.
Пусть  — конечное множество,
— конечное множество, 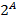 — семейство всех подмножеств
— семейство всех подмножеств 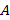 ;
;  — семейство всех
— семейство всех  -элементных подмножеств
-элементных подмножеств 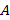 ; «
; « », «
», « », «—» — обычные теоретико-множественные операции объединения, пересечения и дополнения.
», «—» — обычные теоретико-множественные операции объединения, пересечения и дополнения.
Первым объектом при изучении системы 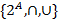 является отображение
является отображение
|
|
|

определяемое следующим образом:

где  — число элементов множества B.
— число элементов множества B.
Задачи первого уровня сложности, связанного с отображением, часто имеют выражение в терминах биномиальных коэффициентов  , имеющих «бытовое» название — «число сочетаний из
, имеющих «бытовое» название — «число сочетаний из  по
по  ».
».
По определению

и комбинаторный смысл этой формулы следующий:  — это число
— это число  -элементных подмножеств
-элементных подмножеств  -элементного множества.
-элементного множества.
Биномиальные коэффициенты в значительной мере представляют собой «базис» элементарной комбинаторики и на их языке формулируются многие факты, представляющие интерес для комбинаторного анализа в целом.
Имеют место следующие хорошо известные и легко проверяемые соотношения:
-
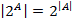 ,
, -
 ,
,
а также простейшие соотношения для биномиальных коэффициентов (б. к.)
-
 ,
, -
 ,
, -
 ,
, -
 ,
, -
 ,
, -
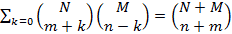 . (1.5)
. (1.5)
Формулы вида (1.5) составляют часть общего класса комбинаторных тождеств, насчитывающих тысячи соотношений подобного рода и играющих значительную роль во многих разделах математики и теоретической физики. Наиболее естественный способ для обоснования приведённых выше формул и получения новых — это метод производящих функций.
Упражнения.
a) Найти число подмножеств из  , содержащих фиксированный элемент
, содержащих фиксированный элемент  .
.
b) Найти число подмножеств  , которые пересекаются с данным подмножеством
, которые пересекаются с данным подмножеством  .
.
c) Найти число решений уравнения

при  и для упорядоченных решений.
и для упорядоченных решений.
d) Найти число решений уравнения
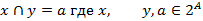
при  и для упорядоченных решений.
и для упорядоченных решений.
e) Найти число неупорядоченных решений уравнения

при 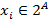 , где
, где 
f) Найти число решений «неравенства» 

g) Найти число подмножеств мощности  , которые пересекаются с данным множеством
, которые пересекаются с данным множеством  , где
, где  ,
,  .
.
Лекция 2. Упорядоченные множества.
Порядок на множествах.
Если перейти от «обычного» конечного множества к частично упорядоченному множеству (Ч.У.М.), то количество и сложность комбинаторных проблем резко возрастает. Понятие упорядоченности (что больше?) играет исключительно важную роль во многих разделах математической науки и, в том числе, в комбинаторном анализе. Поэтому многие из задач, относящихся к Ч.У.М., имеют глубокий математический и содержательный смысл.
|
|
|
Итак, пусть  — множество с бинарным отношением
— множество с бинарным отношением  , удовлетворяющим стандартным требованиям рефлексивности, антисимметричности и транзитивности. Такое множество называется частично упорядоченным или кратко (Ч.У.М.).
, удовлетворяющим стандартным требованиям рефлексивности, антисимметричности и транзитивности. Такое множество называется частично упорядоченным или кратко (Ч.У.М.).
Функция  , определённая на Ч.У.М.
, определённая на Ч.У.М.  соотношением
соотношением
 (2.1)
(2.1)
характеризует «сравнимость» элементов  и называется дзета-функцией.
и называется дзета-функцией.
Если  конечно, то соотношение (2.1) характеризует инцидентность элементов
конечно, то соотношение (2.1) характеризует инцидентность элементов  и может быть описано с помощью соответствующей матрицы
и может быть описано с помощью соответствующей матрицы  , которая и называется матрицей инцидентности Ч.У.М.
, которая и называется матрицей инцидентности Ч.У.М.  .
.
Нетрудно понять, что 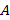 является верхне-треугольной и потому существует обратная матрица
является верхне-треугольной и потому существует обратная матрица  , элементы которой
, элементы которой 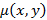 определяют функцию Мёбиуса частичного порядка
определяют функцию Мёбиуса частичного порядка  .
.
Любое подмножество  такое, что элементы
такое, что элементы  попарно сравнимы, образует цепь, то есть
попарно сравнимы, образует цепь, то есть  .
.
Антицепь — это множество из 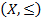 с противоположным свойством, то есть любые два элемента антицепи
с противоположным свойством, то есть любые два элемента антицепи  несравнимы или
несравнимы или

Цепи и антицепи — это подмножества Ч.У.М., в значительной степени характеризующие его структуру, и потому им обычно уделяется внимание при исследовании конкретных Ч.У.М. Одним из самых значительных результатов в теории Ч.У.М., касающихся введённых выше понятий, является следующее утверждение.
Теорема (Дилуорс). Максимальная мощность антицепи в 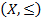 равна минимальному числу непересекающихся цепей, покрывающих
равна минимальному числу непересекающихся цепей, покрывающих  .
.
Доказательство. В одну сторону очевидно: если порядок разбит на k непересекающихся цепей, то любая антицепь пересекается с каждой из цепей не более чем по одному элементу и в антицепи не больше k элементов.
В другую сторону - индукция по числу элементов в порядке.
База — порядок из одного элемента — очевидно выполнена.
Пусть утверждение теоремы справедливо для порядков с количеством элементов не больше n.
Рассмотрим порядок P, в котором n+1 элемент. В любом конечном порядке есть минимальные элементы. Пусть m —минимальный элемент в порядке P. Отбрасывая этот элемент, получаем порядок Q, для которого утверждение теоремы выполнено. Обозначим наибольший размер антицепи в Q через s.
|
|
|
По предположению индукции порядок Q можно разбить на s непересекающихся цепей. Наибольший размер антицепи в P либо равен s, либо равен s + 1.
В последнем случае m содержится в антицепи размера s + 1 и порядок P легко разбивается на s + 1 цепь: одна состоит только из элемента m, а остальные разбивают Q на s непересекающихся цепей.
Осталось рассмотреть случай, когда наибольший размер антицепи в P равен s. Элемент m тогда сравним с какими-то элементами порядка Q, а поскольку он минимальный, то он меньше каких-то элементов. Рассмотрим в каждой цепи в Q минимальный элемент, входящий в антицепь максимального размера. Совокупность всех этих элементов образует антицепь M. Действительно, если для двух таких элементов a < b, то рассмотрим максимальную антицепь, в которой лежит a. Эта антицепь пересекается с цепью, в которой лежит b.
В силу минимальности b по транзитивности получаем сравнимость двух элементов антицепи, что дает противоречие. Один из элементов q построенной антицепи M сравним с m (иначе в P есть антицепь размера s+1).
То есть, получается, что m < q, а все элементы, меньшие q в цепи C разбиения Q на s непересекающихся цепей, не входят в антицепи размера s. Выделим цепь, состоящую из m и всех элементов цепи C, начиная с q и больше. Порядок на оставшихся элементах не содержит антицепей размера s (так как любая такая антицепь обязана пересекать остаток от цепи C) и в нем не больше n элементов. Значит, для этого порядка утверждение теоремы справедливо и его можно разбить на s−1 непересекающуюся цепь. Добавляя выделенную цепь, получаем разбиение исходного порядка P на s цепей.
Таким образом, утверждение теоремы справедливо и для порядка P. По принципу математической индукции теорема справедлива для всех конечных порядков.
Теорема доказана.
Мы используем эту теорему для получения следующей известной верхней границы числа антицепей в произвольном конечном Ч.У.М.
Утверждение. Если  — максимальная мощность антицепи в
— максимальная мощность антицепи в  , то для числа
, то для числа 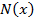 -антицепей в
-антицепей в  справедлива оценка
справедлива оценка
|
|
|
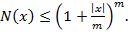
Доказательство. В силу теоремы Дилуорса для  справедливо следующее разложение на множество непересекающихся цепей:
справедливо следующее разложение на множество непересекающихся цепей:

Каждая антицепь в  содержит не более одного элемента из каждой цепи
содержит не более одного элемента из каждой цепи  . Отсюда получаем границу
. Отсюда получаем границу

Здесь мы использовали неравенство о среднем арифметическом и среднем геометрическом и дизъюнктивность  , то есть
, то есть

Мощность максимальной антицепи в  оценивается в следующем утверждении, которое называется леммой Шпернера.
оценивается в следующем утверждении, которое называется леммой Шпернера.
Лемма Шпернера. Если  — антицепь в
— антицепь в  , то
, то

Доказательство. Общее число цепей длины 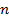 , «соединяющих» точки
, «соединяющих» точки 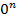 и
и  , равно
, равно  . Если
. Если  — антицепь, то число цепей длины
— антицепь, то число цепей длины 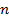 , проходящих через
, проходящих через  , равно
, равно  , и так как все эти цепи различны, то общее число цепей, проходящих черeз
, и так как все эти цепи различны, то общее число цепей, проходящих черeз  , оценивается как
, оценивается как
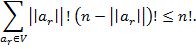
Отсюда получаем
 (2.2)
(2.2)
Так как  , то из (2.2) следует
, то из (2.2) следует

что и требовалось доказать.
Так как любой слой  в
в  является антицепью, то лемму Шпернера можно уточнить следующим образом: если
является антицепью, то лемму Шпернера можно уточнить следующим образом: если 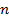 — чётное число, то единственной антицепью мощности
— чётное число, то единственной антицепью мощности  является «слой». Если же
является «слой». Если же 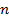 нечётно, то таких антицепей ровно две — это «слои»
нечётно, то таких антицепей ровно две — это «слои» 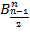 ,
,  .
.
Пусть  — множество натуральных чисел со следующим бинарным отношением:
— множество натуральных чисел со следующим бинарным отношением:  —
—  — делитель
— делитель  . Это отношение порождает отношение частичного порядка на
. Это отношение порождает отношение частичного порядка на  :
:

Множество  с этим отношением порождает дистрибутивную решётку в том смысле, что для любой пары натуральных чисел существует единственный минимальный (в смысле введённого порядка) и единственный максимальный элемент. Этими элементами являются классические теоретико-числовые функции: наибольший общий делитель и наименьшее общее кратное. Если же рассмотреть только ограниченный интервал
с этим отношением порождает дистрибутивную решётку в том смысле, что для любой пары натуральных чисел существует единственный минимальный (в смысле введённого порядка) и единственный максимальный элемент. Этими элементами являются классические теоретико-числовые функции: наибольший общий делитель и наименьшее общее кратное. Если же рассмотреть только ограниченный интервал  натурального ряда с этим же отношением частичного порядка, то множество
натурального ряда с этим же отношением частичного порядка, то множество  будет также Ч.У.М., но уже не будет решёткой. Если [a, b] — интервал в
будет также Ч.У.М., но уже не будет решёткой. Если [a, b] — интервал в  , то «длина» этого интервала равна
, то «длина» этого интервала равна  то есть
то есть

где  —теоретико-числовая функция — число всех делителей
—теоретико-числовая функция — число всех делителей  . Если [a, b] = [3, 36], то
. Если [a, b] = [3, 36], то  Если [a, b] = [12, 48], то
Если [a, b] = [12, 48], то 
Оценим теперь мощность максимальной антицепи в  . Пусть
. Пусть  =
= 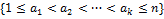 — произвольное подмножество
— произвольное подмножество 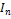 .
.
Определение. Преобразование  — называется сдвигом
— называется сдвигом  .
.
Лемма. Если  — антицепь в
— антицепь в 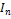 и
и  , то
, то  — антицепь в
— антицепь в 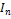 .
.
Доказательство. С одной стороны, ни одно из чисел  не делится на
не делится на  . С другой, если
. С другой, если  — целое число, то из условий
— целое число, то из условий  и
и  следует, что
следует, что  или
или 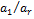 — что противоречит тому, что
— что противоречит тому, что  — антицепь. Таким образом,
— антицепь. Таким образом,  — антицепь.
— антицепь.
Следствие. Если  — антицепь в
— антицепь в 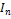 , то
, то 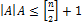 .
.
Доказательство. Из предыдущей леммы следует, что если  — антицепь в
— антицепь в 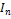 , то
, то  может быть «размещена» в интервале
может быть «размещена» в интервале  , что и завершает обоснование приведённой выше верхней граница. Само «размещение»
, что и завершает обоснование приведённой выше верхней граница. Само «размещение»  проводится путём применения итераций преобразования
проводится путём применения итераций преобразования  .
.
|
|
|
Замечание. Иногда это следствие формулируют в следующей теоретико-числовой форме: если в отрезке [1,  ] выбрать
] выбрать  число, то найдётся пара из них таких, что одно делится на другое.
число, то найдётся пара из них таких, что одно делится на другое.
ЧУМ подслов и фрагментов.
Пусть  — конечный алфавит и
— конечный алфавит и  — множество всех слов конечной длины над алфавитом
— множество всех слов конечной длины над алфавитом  . Под конкатенацией (произведением) слов
. Под конкатенацией (произведением) слов  будем понимать слово
будем понимать слово  . При этом удобно ввести понятие пустого слова
. При этом удобно ввести понятие пустого слова 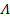 , которое обладает следующим свойством:
, которое обладает следующим свойством:

для любого слова  .
.
Множество  с операцией конкатенации образует моноид. Если
с операцией конкатенации образует моноид. Если  , где
, где  , то слово
, то слово  называется подсловом или фактором слова
называется подсловом или фактором слова  .
.
Если же  и
и  , где
, где  , то
, то  — это фрагмент слова
— это фрагмент слова  . Ясно, что каждое подслово слова
. Ясно, что каждое подслово слова  является одновременно и фрагментом
является одновременно и фрагментом  . Таким образом, и подслово, и фрагмент являются частями исходного слова, которые несут об этом слове определённую информацию.
. Таким образом, и подслово, и фрагмент являются частями исходного слова, которые несут об этом слове определённую информацию.
Если  , то длина слова
, то длина слова  по определению равна
по определению равна 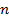 . При этом используется обозначение
. При этом используется обозначение

Отображение

является гомоморфизмом моноида  в полугруппу натуральных чисел
в полугруппу натуральных чисел  . При этом выполнены очевидные соотношения.
. При этом выполнены очевидные соотношения.
1) 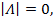
2) 
3) 
Бинарные отношения «быть подсловом» и «быть фрагментом» превращают моноид  в частично-упорядоченное множество. Диаграммы Хассе этих частичных порядков существенно различаются.
в частично-упорядоченное множество. Диаграммы Хассе этих частичных порядков существенно различаются.
1) Частичный порядок — быть подсловом.
Мы будем писать
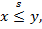
если слово  является подсловом слова
является подсловом слова  .
.
Пусть  и
и  — множество всех слов длины
— множество всех слов длины  над бинарным алфавитом. Диаграмма Хассе Ч.У.М.
над бинарным алфавитом. Диаграмма Хассе Ч.У.М.  выглядит следующим образом (рис. 1):
выглядит следующим образом (рис. 1):

Общая геометрическая характеристика диаграммы Хассе частичного порядка  состоит в следующем.
состоит в следующем.
a) Степень исхода вершины  равна четырём, если
равна четырём, если  и равна трём, если
и равна трём, если  , где
, где  .
.
b) Степень захода вершины  равна единице, если
равна единице, если  и равна двум, если
и равна двум, если  .
.
Таким образом, «вверх» из каждой вершины этой диаграммы Хассе идут три или четыре ребра, а «вниз» — одно или два ребра.
|
|
|


