 |
Корректирующие способности кодов.
|
|
|
|
Очевидно, что параметры (n, M, d)-кода зависят друг от друга, отсюда следует, что для каких-то значений этой тройки параметров коды существуют, а для каких-то нет. В приведенном выше примере декодирования на основе таблицы декодирования был построен (5,4,3)- код. Уже из определения таблицы декодирования и описанной выше схемы следует, что, например, (5,4,5)-код построить нельзя, так как для любого (5,4, d)- кода в столбце таблицы декодирования будет 7 элементов, а в шаре радиуса 2, который требуется для (5,4,5)-кода, 15 точек.
В этом разделе будут приведены несколько утверждений, которые помогают ответить на вопрос о существовании кода с заданными параметрами.
Но для начала сформулируем очевидное утверждение.
Определение. Код называется кодом, исправляющим t ошибок, если алгоритм декодирования правильно декодирует все слова, в которых при передаче по каналу произошло не более t ошибок.
Утверждение. (n, M, d)-код – код с исправлением  ошибок.
ошибок.
Замечание. Есть еще коды, обнаруживающие ошибки.
Опр. Код называется кодом, обнаруживающим t ошибок, если в случае, когда
произошло не более t ошибок, декодер выдает сообщение об ошибке.
Утверждение. (n, M, d)-код обнаруживает  ошибку.
ошибку.
Лекция 13. Теорема Шеннона для канала с шумом.
Введение.
Есть несколько теорем Шеннона. Одна была рассмотрена выше (теорема Шеннона для канала без шума). Здесь мы докажем еще одну теорему Шеннона и об одной просто упомянем. (Эти теоремы известны как теоремы Шеннона для канала с шумом.)
В теореме Шеннона для канала с шумом будет показано, что существуют коды, когда для любого ε>0 при V(C)< 1- H(p) вероятность ошибки декодирования не более ε.
Рассмотрим некоторый код C = { x 1… xM }, где { x 1… xM }– кодовые слова (вектора Bn).
|
|
|
Применяем декодирование в ближайшее слово (по принципу наибольшего правдоподобия и согласно приведенной выше схеме декодирования, а,в случае нескольких вариантов, в кодовое слово с наименьшим номером). Обозначим через T(C) таблицу декодирования.
Передача Прием
a x 1 T(C) – таблица
 b x 2
b x 2
… …
… xM
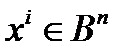
Зададим некоторое ρ>0. Тогда в ситуации 1 таблица Tρ(C) состаляется так, чтобы под каждым кодовым словом 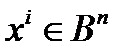 в столбце находились все слова из Sρ (x i), а в ситуации 2 работают эвристические правила, примеры которых приведен выше.
в столбце находились все слова из Sρ (x i), а в ситуации 2 работают эвристические правила, примеры которых приведен выше.
Замечание.
Подчеркнем еще раз, что кодом называется любое подмножество булева куба Bn мощностью M. Поэтому не любой код будет кодом, исправляющим ошибки. Но к любому коду можно формально применить описанную выше схему декодирования. Все точки кода окружаем шарами радиуса ρ, а полученный вектор декодируем в центр шара. Если же вектор попадает в несколько кодовых шаров, то, возможно, что произошла ошибка декодирования. Правило, по которому в этом случае декодер производит декодирование несущественно. Например, применяется какое-нибудь дополнительное правило декодирования: в случайный, в ближайший и т.п.
Возьмем точку x в Bn и шар S[ pn] (x) радиуса [ pn] с центром в этой точке. Оценим число точек в нем.
Лемма 13.1. Справедливо неравенство
| S[ pn] (x)| ≤ 2 nH ( p )
Доказательство. | S[ pn] (x)| =  .
.
Вспомним, что 0 ≤ p < 1\2. Согласно принципу наибольшего правдоподобия – декодирование в ближайшее кодовое слово – выполняется соотношение
(1 – p)n ≥ p(1 – p)n-1 ≥ … ≥ pk(1-p)n-k.
|
|
|
Отсюда следует.

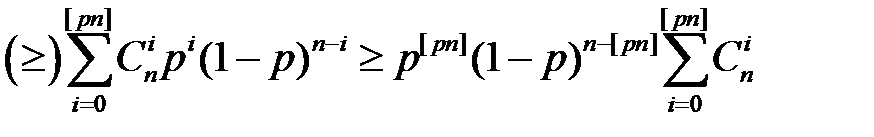 ,
,
где  - мощность шара радиуса [pn].
- мощность шара радиуса [pn].
Тогда | S [ pn ](x)| ≤ (p [ pn ] (1 – p) n – [ pn ])-1 =  ≤ 2 nH ( p ).
≤ 2 nH ( p ).
Лемма доказана.
Комбинаторное доказательство.
Теорема 13.1. (Вторая теорема Шеннона).
Для любого R: 0 < R < C (ρ), такого что M=2[nR], выполняется соотношение:
P *(M, n, p)  1.
1.
Доказательство.
Пусть имеется код Vk  L={
L={  }. Напомним, что P (Vk) – вероятность правильного декодирования для Vk.
}. Напомним, что P (Vk) – вероятность правильного декодирования для Vk.
Рассмотрим 3 функции:

Пусть Ak(i) – число векторов в Bn, находящихся на расстоянии i от некоторого кодового слова кода Vk и декодируемых в это кодовое слово.
Тогда P (Vk) = 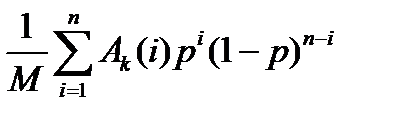 - вероятность правильного декодирования Vk. Здесь
- вероятность правильного декодирования Vk. Здесь 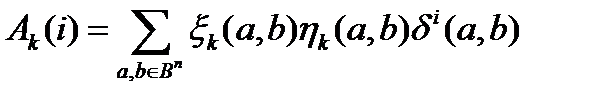 . Действительно, каждое слагаемое в этой сумме равно единице, если выполняются все три условия:
. Действительно, каждое слагаемое в этой сумме равно единице, если выполняются все три условия:
1)  ,
,
2) расстояние от a до b равно i,
3) b декодируется в a.
В формуле для вероятности правильного декодирования P (Vk) параметр Ak(i) – это число точек из 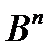 , которые находятся на расстоянии i от некоторого кодового слова и декодируются в это кодовое слово.
, которые находятся на расстоянии i от некоторого кодового слова и декодируются в это кодовое слово.
Всего таких кодов  :
:  ,
,  .
.
Усредняем вероятность правильного декодирования по всем кодам и получаем среднюю вероятность правильного декодирования


 =
= 
 (13.1)
(13.1)
Рассмотрим саму внутреннюю сумму в последней формуле приведенных выше выкладок. Эта сумма равна числу кодов Vk таких, что  , и b декодируется в a. Заметим, что точка b обязательно декодируется в a тогда и только тогда, когда в коде Vk нет кодовых точек расположенных к b ближе, чем точка a. Это означает, что в шаре (обозначим его S(a,b)) радиуса ρ(a,b) с центром в точке b нет других точек кода Vk. Поэтому, если точки a, b фиксированы, то остальные (M -1) точку кода мы можем выбирать произвольным образом из множества Γ= Bn\ S(a, b). Мощность этого множества
, и b декодируется в a. Заметим, что точка b обязательно декодируется в a тогда и только тогда, когда в коде Vk нет кодовых точек расположенных к b ближе, чем точка a. Это означает, что в шаре (обозначим его S(a,b)) радиуса ρ(a,b) с центром в точке b нет других точек кода Vk. Поэтому, если точки a, b фиксированы, то остальные (M -1) точку кода мы можем выбирать произвольным образом из множества Γ= Bn\ S(a, b). Мощность этого множества  , где
, где  количество точек из
количество точек из 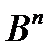 в шаре радиуса ρ. (Так как это количество не зависит от x, а зависит только от n и ρ, то, чтобы подчеркнуть этот факт, ниже при необходимости мы наряду с обозначением
в шаре радиуса ρ. (Так как это количество не зависит от x, а зависит только от n и ρ, то, чтобы подчеркнуть этот факт, ниже при необходимости мы наряду с обозначением  будем пользоваться и другим -
будем пользоваться и другим -  ). Отсюда следует, что упомянутая внутренняя сумма равна
). Отсюда следует, что упомянутая внутренняя сумма равна  .
.
Отметим два комбинаторных факта и продолжим начатую выше цепочку соотношений.
1) Число пар точек из 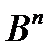 , лежащих на расстоянии i равно
, лежащих на расстоянии i равно 
2) Справедливо известное комбинаторное равенство

Далее из (13.1) имеем
(=) 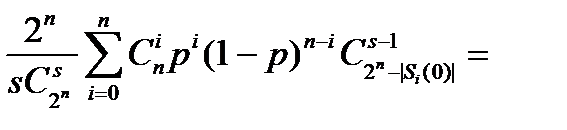
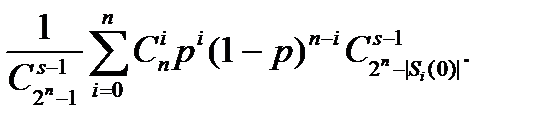 (13.2)
(13.2)
Мы доказали одно из основных равенств, которое будем использовать ниже.
|
|
|
Отметим несколько моментов:
1) Функция  выпукла вверх.
выпукла вверх.
2) Тогда функция  выпукла вниз.
выпукла вниз.
3) Сумма выпуклых функций выпукла.
4) Выпуклая функция от выпуклой функции выпукла.
5) Отсюда следует, что функция f(i)=  является функцией, выпуклой вниз.
является функцией, выпуклой вниз.
6) Вспомним неравенство Йенсена. Пусть даны числа α 1 … αn, αi> 0, 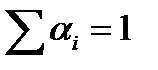 . Тогда для выпуклой вниз функции f(x) справедливо неравенство.
. Тогда для выпуклой вниз функции f(x) справедливо неравенство.


7) В качестве α i возьмем  . Очевидно, что
. Очевидно, что  , а
, а  .
.
Используя 1-7, получим
 . (13.3)
. (13.3)
Далее используем очевидные соотношения
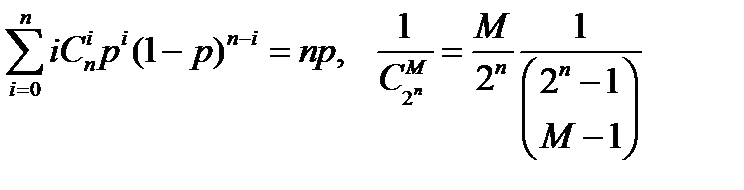 . (13.4)
. (13.4)
Заметим далее, что максимальная вероятность больше средней, т.е.
P *(M, n, p)≥  .
.
Из этого факта и соотношений (13.2), (13.3), (13.4) получаем:
P *(M, n, p) ≥ =  .
.
Далее



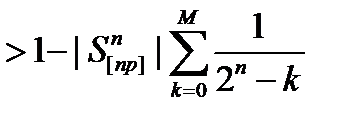 =
=  ≥
≥ 
Теперь устремляем n→∞ и раскладываем в ряд, оставляя главные члены каждого слагаемого. Получаем
 = 1- (
= 1- (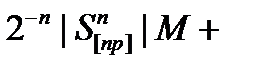

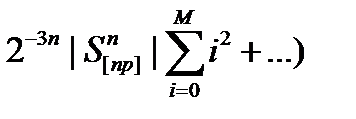 =
=
=1-  О(
О( ),
),
Что асимптотически при n→∞ равно

Вспомним лемму (13.1):
| S[ pn] (x)| ≤ 2 nH ( p ).
Кроме того, заметим, что по условию: 0 < R < C (ρ), M=2[nR].
Отсюда получаем
 ≥
≥ 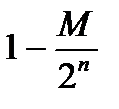 2 nH ( p ) ≥
2 nH ( p ) ≥ 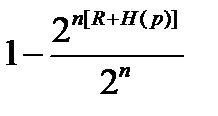 = 1- 2 n(R-C(p)).
= 1- 2 n(R-C(p)).
Таким образом мы доказали, что при 0 < R < C (p) и n→∞ справедливо неравенство
P *(M, n, p)> 1- 2 n(R-C(p)).
Но это значит, что P *(M, n, p) →1 при n→∞.
Теорема доказана.
Дополнения и замечания.
Теорема Шеннона – это теорема существования, и она не дает методов построения кодов. Разбор, классификация и общее представление совокупности таких методов – предмет отдельной дисциплины – теории кодирования.
А что будет, если R>C(p)? На этот вопрос отвечает третья Теорема Шеннона.
Теорема 13.2. (Третья теорема Шеннона.) Для любого R: R > C (p)>0, такого что M=2[nR], не существует кода C, для которого бы выполнялось соотношение:
PC (M, n, p) →1 при n→∞.
Мы оставим эту теорему без доказательства.
Доказательство этой теоремы базируется на нескольких фактах (см. [7]). В лемме 13.1 было доказано, что | Bpn (x)| ≤ 2 nH ( p ). На самом деле, справедлива более точная оценка: | Bpn (x)| ~ 2 nH ( p ) (при n → ∞). И это асимптотическое равенство достигается для совершенных кодов (см. ниже). В итоге получим, что
|
|
|
k = n – n H (p)
для совершенного кода. А отсюда можно получить, что максимум вероятности правильного декодирования достигается именно на совершенном коде. После этого в качестве кода C при доказательстве теоремы можно брать только совершенный код. А это уже конструкция с определенными свойствами, которые и используются для доказательства теоремы.
|
|
|


