 |
Лекция 4. Кодирование слов. Комбинаторика слов и фрагментов.
|
|
|
|
Кодирование слов.
Как уже выше говорилось, любая информация может быть представлена словом в конечном алфавите. Есть объект O, субъект S, а перед субъектом стоит задача Z, связанная с данным объектом. Субъект решает эту задачу с помощью алгоритма A(Z), входом которого является информация об объекте в виде слова I(O). Как мы уже выше видели на примерах чисел, графов и признаковых векторов информацию эту об объекте можно представлять по-разному: разными словами в разных алфавитах. Предполагается, конечно, что любое такое представление дешифруемо, неизбыточно и разумно.
Но предположим, что имеется критерий предпочтения одних представлений другим, например, минимизация длины этого самого слова-представления. Возникает задача преобразования одного слова I(O) в другое J(O).
В этом случае рассматривается следующая модель. Есть два алфавита
А = (а 1, …, а n) и B = (b 1, …, bq).
Кодирование φ это отображение слов α в алфавите А в слова β=φ(α) в алфавите В.
Кодирование будет дешифруемым, если по слову β однозначно восстанавливается α. Тогда отображение φ – биекция.
Например, у нас есть кодируемые объекты x - слова в алфавите A. Есть другой алфавит, например, бинарный. Нельзя ли найти минимальную длину K(x) кода объекта x, пусть даже в другом алфавите B?
Простейший случай. Есть два алфавита. Когда кодирование более «экономно»?
Пример. Сериальное кодирование.
Здесь А = (0,1) и B = (0,1,…,9,*). Символ * играет роль разделителя.
В данном примере битовые последовательности кодируются натуральными числами. Как это следует из свойств данного кодирование, оно дает эффект сжатия, когда битовые последовательности представляют собой чередование сравнительно больших блоков нулей и единиц.
|
|
|
Алгоритм кодирования. Пусть дана битовая последовательность α и а 
(0,1) ее первый символ. Серией назовем часть последовательности, состоящую из одинаковых символов. Тогда любую битовую последовательность можно представить, как чередование серий из нулей и единиц. Пусть в последовательности α всего S серий, длина первой - x1, длина второй - x2,…, длина S–й - xS. Тогда кодом α будет слово β=φ(α)=а* x1* x2*…* xS.
Алгоритм декодирования очевиден.
Ниже мы более подробно проанализируем свойства сериального кодирования.
Слова и языки
Существует много способов получать из одних слов другие слова. Так возникают специальные классы слов, языки и другие алгебраические конструкции. На эту тему у вас был обширный и глубокий курс лекций и семинаров. Приведем лишь несколько примеров.
Пример. Если 
и 
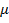—морфизм,
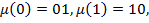
то итерации морфизма 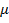порождают слова по стандартным правилам:
,
,
,
.
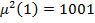Аналогичным образом могут быть найдены все итерации морфизма 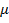. Бесконечные слова 
и 
называются словами Туэ — Морзе.
Другим способом построения языков является использование частей одного и того же слова.
Пример. Пусть 
и 
. Рассмотрим последовательность всех фрагментов длины 
слова 
, выписанных в лексикографическом (по способу построения) порядке:
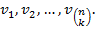
Положим по определению
Таким образом, 
— это конкатенация всех фрагментов длины у слова , выписанных в лексикографическом порядке. Длина слова равна 
.
Применяя к слову то же самое преобразование, мы получим слово 
. Так формируется язык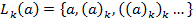 
.
Отметим далее, что отображение 
:
(4.1)
заданное формулой (4.1), является линейным, и если фрагменту 
сопоставить матрицу 
такую, что
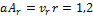
то матрица 
линейного преобразования является конкатенацией матриц , то есть
Пример
1) Пусть 
, 
и фрагменты длины два упорядочены лексикографически: 
, 
, 
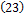. Фрагмент реализуется матрицей 
, — 
, — 
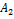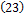, где
|
|
|
Поэтому матрица линейного преобразования
выглядит так:
Ясно, что
«Геометрические» свойства преобразования описываются в следующих утверждениях.
Предложение. 
Доказательство. Пусть 
. Тогда число фрагментов длины 
у слова 
, имеющих вес, равный 
, равно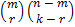 
. Поэтому
Предложение. 
Предложение. 
.
Выбор фрагмента в качестве «части» слова при построении языка 
является реализацией лишь одного из возможных способов построения языка, исходя из фиксированного слова и его частей.
Выбрав вместо фрагмента «подслово» фиксированной длины, можно получить другие языки с теми или иными структурными особенностями.
Разумеется, существует много разных формальных языков и много разных конструкций, позволяющих строить и анализировать эти языки.
Слова и фрагменты
Если 
, то под биномиальным коэффициентом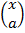 
понимается число вхождений слова в качестве фрагмента в слово 
. Так как
то функция 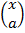является, в определённом смысле, обобщением биномиального коэффициента, что и послужило основанием для использования классического обозначения .
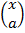Для произвольного слова 
множество чисел вида 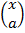, где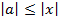 
, называются параметрами Уитни слова . Эти параметры играют значительную роль как в комбинаторике слов, так и в различных приложениях.
Пример
2) 
, 
,
, 
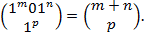
Следующие свойства являются прямыми следствиями определений:
1) 
;
2) 
, 
;
3) 
.
Здесь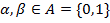 
, 
— символ Кронекера.
Далее в этом разделе всюду рассматривается только двоичный алфавит.
Обсудим теперь следующую проблему: как формально описать вычисление биномиального коэффициента
Пусть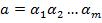 
и
Лемма. Справедлива формула
(4.2)
Формула (4.2) свидетельствует о том, что биномиальный коэффициент может быть выражен в виде полинома от переменных 
с целыми коэффициентами.
Следствие. Справедливы соотношения
Лемма дается без доказательства. Доказательство соотношений из данного следствия можно провести без использования леммы. Это предлагается вам сделать в качестве задач из задания. Сделав эти задачи, вы легко поймете смыл формулы (4.2).
Полином 
может быть представлен в виде суммы моногенных слагаемых, по которым восстанавливается весь полином. Возвращаясь к предыдущему примеру, мы находим эти полиномы в следующей форме:
|
|
|
или, что то же самое,
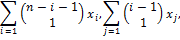
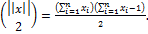
В общем виде ситуация выглядит следующим образом.
Лемма. Справдлива формула
Здесь 
— подпоследовательность последовательности 
.
Доказательство. Так как 
— подпоследовательность , то 
может быть выбран 
-способами, 
— 
-способами, …, 
— 
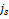-способами. Что и требовалось доказать.
Утверждение. Если 
— номера единиц в слове 
и 
, то
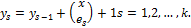
Доказательство этого утверждения будет приведено в следующих лекциях. Смысл утверждения состоит в том, что номера единичных букв в слове могут быть выражены в терминах числа фрагментов определённого вида и длины. В частности, если 
, то слово , как будет показано далее, может быть восстановлено по фрагментам длины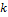 
.
|
|
|
