Лекция 5. Примеры кодирований: сериальное кодирование, кодирование натуральных чисел, побуквенное кодирование.

Сериальное кодирование.

Определение сериального кода было дано в предыдущей лекции. Рассмотрим его свойства.

Определение.      Длиной сериального кода назовем число где

 [ log x]*=1 при x=1 и [ log x]*= [ log x] при x>1.

Определение. Средней длиной кода для n-последовательностей назовем число

,

Где сумма берется по всем двоичным последовательностям длины n.

Свойства такого кодирования иллюстрируются следующими двумя утверждениями.

Утверждение. Если все x_i=1, то l(α)=|α|.

Утверждение. Если все x_i>1, то .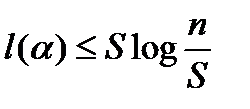

Доказательство.

.

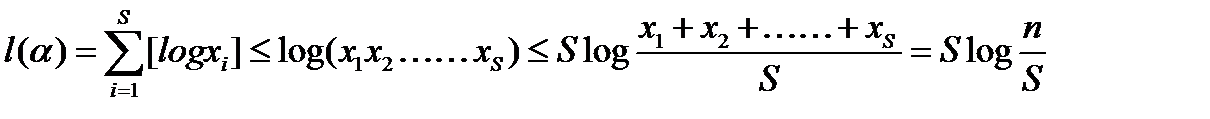Утверждение. Средняя длина слова с S сериями в сериальном кодировании
              .

Утверждение. Справедлива асимптотическая оценка

 

Из этих утверждений следует.

Таким образом, сериальное кодирование при малых количествах серий и большой длине серий приводит к тому, что при таком кодировании возникает эффект сжатия.

Если серии короткие и их много, например:  и , то эффекта сжатия не возникает.

Пусть  — число слов из  веса , имеющих ровно  серий.

Лемма. Справдлива формула

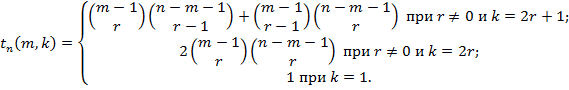 (5.2)

Доказательство. Если слово  имеет  серий, то

 

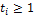где  и  и  для .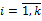

При этом если , то

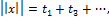
и если , то

Далее, если  и , то  равно числу решений системы уравнений:

 (5.3)

Если , то (5.3) переходит в следующую форму:

 (5.4)

Число неизвестных в первом уравнении равно , а во втором — .

Так как множества неизвестных не пересекаются, то число решений системы (5.4) равно . Если  и , то  равно числу решений системы уравнений

или

 (5.5)

Таким образом, число решений системы (4.5) равно . Поэтому в случае , то есть , число  задаётся следующей формулой:

при 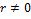. Если же , то есть , то .

Если же , то есть , то, повторяя предыдущие рассуждения, получаем следующее выражение для :

Окончательно получаем формулу (5.2).

Лемма доказана.

Коды натурального ряда.

Здесь мы будем рассматривать алфавиты А = (0,1,…,9)  и B= (0,1).

Задача кодирования натуральных чисел битовыми последовательностями актуальна, так как часто необходимо хранить и передавать информацию в бинарном виде. Особенно остро она встала в 50-е годы прошлого века в связи с распространением компьютеров.

В данной модели предполагается, что нужно работать (хранить, передавать) с битовой информацией, изначально представимой, например, в десятичных числах. При этом набор чисел представляется битовой последовательностью без разделителей.

Простой переход к двоичной записи не обеспечивает префиксности, а, следовательно, и декодируемости этой битовой последовательности.

Приведем примеры кодов, которые это обеспечивают.

Пусть n > 1, двоичную запись числа n обозначим BIN(n) = α ₁… α_n, α _i {0, 1}. (Например, BIN(30) = 11110, BIN(75) = 1001011). Заметим, что k = |BIN(n)| = [log n ] + 1. Пусть B(n) – двоичная запись n без первого символа. (Например, B(30) = 1110, B(75) = 001011). Тогда |B(n)| = [log n ].

Так как любая двоичная запись натурального числа начинается с единицы, то префиксность можно обеспечить с помощью тривиального кода

TK(n)= 0…0BIN(n),

Где число нулей префиксе равно [log n ] + 1. Длина такого кода 2[log n ] + 2. Следующие два примера дают более экономное кодирование.

Код Элайеса.

Код Элайеса неотрицательного целого числа n обозначим через El (n). Положим El (0) = 10, El (1) = 11.

Пусть n > 1. В этом случае длина слова BIN(n) больше единицы. Код Элайеса состоит из трех фрагментов. Вначале идет некоторое количество нулей, подсчитав которые, мы найдем число символов в двоичной записи |BIN(n)|. Для экономии, учитывая предыдущее замечание можно взять количество нулей на единицу меньшее числа символов в двоичной записи |BIN(n)|. (Так как любая двоичная запись начинается с единицы, то мы всегда знаем, где заканчивается наша цепочка нулей). Теперь мы это количество символов записи |BIN(n)| отсчитываем после последнего нуля, а затем полученный фрагмент из нулей и единиц переводим в десятичную запись и получаем длину закодированного слова. Зная эту длину, мы отсчитываем нужное нам число символов, а полученный фрагмент и будет двоичной записью закодированного натурального числа. Опять же для экономии первую единицу данного фрагмента можно в коде опустить.

Тогда El (n)= 00…0 BIN([log n ]+1) B (n), где 00…0 – маркер, необходимый для того, чтобы знать, сколько последующих за 0 символов может задавать  длину записи числа. Поэтому в данном коде количество нулей перед BIN([log n ]+1) равно |BIN([log n ]+1)|-1.

Примеры (пробелы стоят только для иллюстрации):

El (5) = 0 11 01.

El (75) = 00 111 001011.

Утверждение. Длина | El (n)| не превосходит log n + 2 log (log n) + 3.

Код Левенштейна

В коде Элайеса мы сэкономили по сравнению с тривиальным кодом за счет уменьшения префикса. В коде Левенштейна эта идея доведена до определенного истощения: от двоичной записи числа мы сначала переходим к двоичной записи длины BIN(n) (это было и в коде Элайеса), но затем мы переходим к длине длины, длине длины длины и т.д.

Введем для удобства формальной записи этой идеи некоторые обозначения. Пусть λ ₀(n) = [log n ]. А далее по аналогии до   λ ^k ₀(n) = λ ₀ (λ ^{k -1}₀(n)) = [log…[log n ]].

Для любого n существует S такое, что: λ ^S ₀(n) = 0, λ ^{S -1}₀(n) = 1.

Положим Lev (0)=0, Lev (1) =10. Пусть n > 1. Тогда для такого сила вышеупомянутый параметр S>1. Если в префиксе кода мы ставим S подряд идущих единиц, а затем ноль (чтобы показать, где эта цепочка единиц заканчивается), то это не может быть ни кодом 0, ни кодом 1. А так как λ ^S ₀(n) = 0, λ ^{S -1}₀(n) = 1, то эти соотношения никакой информации для кодирования не содержат, и в код надо включать информацию о длинах, начиная с B (λ ^{S -2}₀(n). Отсюда и следует формула для кода Левенштейна.

Lev (n) = 11…10 B (λ ^{S -2}₀(n))… B (λ ₀(n)) B (n),

где 11…10 – слово из S единиц и одного нуля.

Утверждение.  Длина кода Левенштейна задается соотношением

| Lev (n)| = log n + log log n + o(log log n).

Пример (пробелы только для иллюстрации):

  Lev (75) = 11110 0 11 001011                        

S = 4

Lev(5)=1110 0 01. Lev(62)=11110 0 01 11110.

Побуквенное кодирование.

Мы видели, что при словарном кодировании объектов найти код минимальной длины – это решить алгоритмически неразрешимую проблему. В такой ситуации уместна более слабая постановка задачи. Так как кодирование – это отображение одного множества слов в другое, то ослабление задачи заключается в наложении ограничений на вид такого отображения.

В предыдущей лекции мы рассмотрели два примера таких ограничений: сериальное кодирования и кодирование натурального ряда. Второй из этих примеров является частным случаем более общей ситуации: префиксного кодирования.

Если пренебречь разделителями, то в качестве двух алфавитов возьмем алфавиты

А = (а ₁, …, а _n) и B = (b ₁, …, b_q).

Алгоритм побуквенного (алфавитного) кодирования. Каждой букве a_i алфавита A ставится в соответствие B_i= φ(a_i) – слово в алфавите B длины l_i.

Алфавитное кодирование будет дешифруемым, если отображение  таково, что для .

 

Заметим, что в приведенном определении термин дешифруемость используется в другом смысле, нежели выше при описании основных свойств кодирования (дешифруемость – неизбыточность - разумность). Поэтому в других учебниках используются иные термины, например, разделимость. Но не будем загромождать изложение терминами, тем более, что из контекста всегда ясно, о чем идет речь.

Обратим внимание на следующий важнейший факт, который, по сути дела, и оправдывает интерес к такому виду кодирования. Очевидно, что ограничение на вид отображения φ сразу влечет дешифруемость однобуквенных (в алфавите А) слов. Но из дешифруемости однобуквенных слов сразу следует дешифруемость слов (в алфавите A) любой длины.

Заметим также, что в случае дешифруемого кодирования все слова B_i= φ(a_i) обязательно различны.

Оказывается, что дешифруемость накладывает ограничение на набор длин кодовых слов. Об этом говорит утверждение, известное как неравенство Крафта.

Теорема. Если алфавитное кодирование с длиной кодов l ₁, …, l_n дешифруемо, то выполняется неравенство:

Доказательство. Пусть А = (а ₁, …, а _n) и B = (b ₁, …, b_q). Каждой букве a_i алфавита A ставится в соответствие B_i= φ(a_i) – слово в алфавите B длины l_i. Положим

 Пусть . Возведем Z в некоторую степень m, тогда

.

Здесь введено обозначение S (n, t) – число слов длины t и вида B_{i 1} B_{i 2} … B_in. Из дешифруемости следует, что все такие слова различны, но число различных слов длины t в алфавите из q букв не превосходит q^t, поэтому

S (n, t) q^t.

Тогда , где m – натуральное, а    l ≥ 0, целое. Это неравенство должно выполняться для любого m, но это возможно только тогда, когда Z не превосходит единицы, т.е.

.

Теорема доказана.

Напомним, что слово α является подсловом слова β, если существуют слова γ и δ (возможно пустые) такие, что β=γαδ. Если γ- пустое слово, то слово α называется префиксом слова β.

В общем случае из неравенства Крафта не следует дешифруемость.

Определение. Кодирование называется префиксным, если ни одно из кодовых слов не является началом другого.

Теорема. Префиксный код дешифруем.

Доказательство: Пусть есть α и β – два слова:

Покажем, что  из равенства φ (α) = φ (β)следует равенство α = β.

Пусть  

Поочередно слева направо сравниваем подслова слов α и β, используя знание функции ϕ, которая определяет наше побуквенное кодирование (эта функция позволяет находить B_i= φ(a_i) среди подслов слов α и β. Сначала сравниваем  и  , затем переходим к   и  и т.д.

Если длины слов  и одинаковы, то сами слова должны быть одинаковыми из того, что  Если длины слов разные, то одно из двух слов:  или – начало другого, что противоречит определению префиксности.

Значит, α = β.

Теорема доказана.

Из теоремы сразу следует алгоритм декодирования префиксного кода.

Алгоритм декодирования. Берем первый символ слова φ (α)и ищем однобуквенное слово среди кодовых слов. Если находим такое слово, например, B_i= φ(a_i), то декодируем слово B_i= φ(a_i) в букву a_i и продолжаем работать, начиная со следующего символа слова φ (α). Если не находим, то добавляем следующий символ и ищем среди кодовых слов уже двухбуквенное слово. И т.д.

В случае алфавитного кодирования можно ограничиться префиксными кодами, так как, в каком-то смысле, любой дешифруемый алфавитный (побуквенный) код можно «свести к префиксному». А существование префиксного кода полностью определяется неравенством Крафта.

Теорема (о существовании префиксного кода). Префиксный код с длинами кодов l ₁ … l_n существует тогда и только тогда, когда выполняется неравенство Крафта

.

Доказательство. Т.к. префиксный код дешифруем, то выполняется неравенство Крафта. С другой стороны, пусть выполняется неравенство Крафта. Покажем, что в этом случае существует префиксный код. Мы просто опишем алгоритм построения такого кода, т.е. построим отображение B_i= φ(a_i).

Пусть . Пусть среди чисел l ₁ … l_n имеется S ₁ единиц, S ₂ двоек, S ₃ троек и т.д. до S _l слов длины l.  При этом некоторые из S _i могут быть нулями. Упорядочим B_i= φ(a_i) по возрастанию длины.

B ₁ = | l ₁| = 1

B ₂ = | l ₂| = 1  S ₁ слов длины 1

…

B_{S 1}= | l_{S 1}| =1

B _{S 1+1} = | l _{S 1+1}| = 2 S ₂ слов длины 2

…

 

Тогда левую часть неравенства Крафта можно представить в виде:                                                                                                            

              S ₁                               S ₂                           S ₃

Теперь пошагово строим наш префиксный код.

Первый шаг: Любые S ₁ букв в B  можно использовать для кодирования слов длины. Это следует из того, что при выполнении неравенства Крафта справедливо соотношение: S ₁/ q ≤ 1, из которого следует, что   S ₁ ≤ q. Таким образом мы получили первую группу однобуквенных слов.

Второй шаг:  Аналогично из неравенства Крафта получаем S ₁/ q + S ₂/ q ≤ 1. Отсюда S ₁ q + S ₂ ≤ q ², S ₂ ≤ q ² – s ₁ q. Поэтому можно взять S ₂ слов длины 2 в алфавите B так, что они не начинаются со слов первой группы. Таким образом мы получили вторую группу двухбуквенных слов.

Третий шаг: На этом шаге строим группу трехбуквенных слов так, чтобы они не начинались с ранее построенных слов. Такие трехбуквенные слова в нужном количестве существуют, так как вновь из неравенства Крафта следует, что S ₁ / q + S ₂ / q + S₃ / q ≤ 1. А это означает, что S₃ ≤ q³ – qS ₂ – q ² S ₁.

Таким образом проходим все l шагов и в результате получаем дешифруемый префиксный код.

Теорема доказана.

Утверждение.  Код Элайеса – префиксный.

Доказательство: Рассмотрим El (n) и El (m). Если хотя бы одно из этих слов начинается с 1, то это либо 0, либо 1. Утверждение доказано. Пусть n, m больше 1, вспомним теорему о дешифруемости кода: El (n) = α ₁… α _k, El (m) = β ₁… β _S (для определенности k ≥ s). Пусть количество 0, с которых начинается α, совпадает с количеством 0, с которых начинается β. (В противном случае сразу следует свойство префиксности кода.) Далее рассмотрим вторые подслова слов El (n) и El (m). Если они не совпадают, то префиксность кода доказана. Если совпадают, то переходим к окончаниям слов. Если они совпадают, то m=n. В противном случае n не равно m. Таким образом, при m≠n выполняется соотношение B (n) ≠ B (m).

Утверждение доказано.

Докажите в качестве упражнения следующее утверждение.

Утверждение.  Код Левенштейна префиксный.

Предыдущая12345678910111213141516Следующая

Поделиться:

Воспользуйтесь поиском по сайту: