Сжатие информации. Энтропия по Шеннону.

Этот теоретический предел возможного сжатия и определяется количеством информации в том слове (множестве слов) с помощью которых информация представлена.

Математическая модель: алфавитное кодирование случайного источника.

Рассмотрим следующую модель. Имеется источник, который поочередно генерирует буквы алфавита A= (a ₁ … a_n) с вероятностями p ₁ … p_n. То есть имеет место следующая ситуация.

Источник

              

Каждая буква a_i генерируется с некоторой вероятностью p_i. Эта вероятность p_i не зависит от того, что выдал источник ранее и что он будет выдавать потом. Она также не зависит от очередности выдачи букв источником и от того, какой по счету от начала выдачи выдана данная буква. Такой источник называется источником Бернулли, что является частным случаем стационарного источника. На практике встречаются и другие источники. Для них приведенный ниже результаты неверны, но могут быть получены их аналоги.

Энтропия по Шеннону

Опр. Энтропией случайного источника (энтропией Шеннона) называется число

H (A) = .

Энтропия по Шеннону и энтропия по Хартли.

Заметим, что Энтропия по Хартли является частным случаем энтропии по Шеннону. Если все , то H (A) = log n, а это и есть Энтропия по Хартли множества из n элементов.В общем случае справедливо следующее утверждение, которое показывает, что энтропия по Хартли является оценкой сверху для энтропии по Шеннону. То есть ситуация равновероятных событий наихудшая с точки зрения информативности.

В следующем и других доказательствах нам потребуется математический факт, известный как неравенство Йенсена. 

Неравенство Йенсена. Пусть даны числа α ₁ … α_n, α_i> 0, 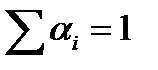. Тогда для выпуклой вверх функции f(x) справедливо неравенство.  

Для выпуклой вниз функции выполняется противоположное неравенство:

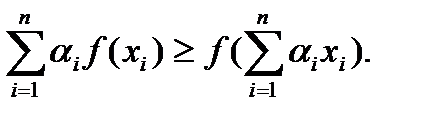
Теорема. Пусть имеется случайный источник, который генерирует буквы алфавита A = (a ₁ … a_n) с вероятностями p ₁ … p_n, тогда справедливо соотношение

H (A) =  .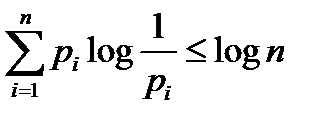

Доказательство. Рассмотрим функцию f (x) = - x log x. Так как f’ (x) = - log x – 1 / ln 2 и f’’ (x) = - 1 / x, то при x ≥ 0 функция f (x) выпукла вверх. Тогда для нее справедливо неравенство Йенсена:   Возьмем α ₁ … α_n, α_i> 0,

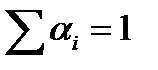
Положим α _i = 1 /n, x_i = p_i,i=1,…,n.

H (A) =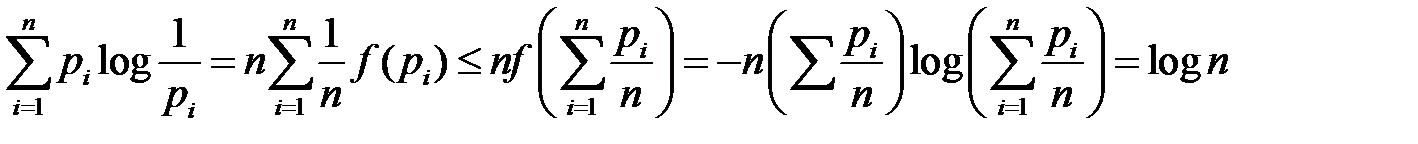

Здесь мы учли, что /n.

Теорема доказана.

Теорема Шеннона

Рассмотрим теперь математическую модель, являющуюся объединением двух предыдущих. Случайный источник генерирует буквы алфавита А = (а ₁, …, а _n), к которым потом применяется некоторый алгоритм алфавитного кодирования φ. (Каждой букве a_i алфавита A ставится в соответствие B_i= φ(a_i) – слово длины l_i в алфавите B = (b ₁, …, b_q)). Как можно оценить качество такого алгоритма?

В случае вероятностного источника такие количественные характеристики алгоритма как 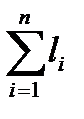или 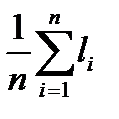 уже не являются информативными, так как не зависят от вероятностей.

В этом случае удобно использовать величину  , которая характеризует среднее количество букв алфавита B, приходящееся на один символ алфавита A при алфавитном кодировании φ. (Назовем эту величину стоимостью кодирования φ). Пусть теперь , где минимум берется по всем возможным дешифруемым алгоритмам алфавитного кодирования (при заданных алфавитах A и B и распределении вероятностей p ₁ … p_n). (Назовем эту величину минимальной стоимостью кодирования).

Если бы мы знали C(A), то смогли бы оценить качество нашего алгоритма φ.

Следующая теорема (она известна под названием теоремы Шеннона для канала без шума) дает ответ на этот практически важный вопрос.

Теорема.  Справедливо соотношение

.

Доказательство.

Сначала докажем оценку снизу:

.

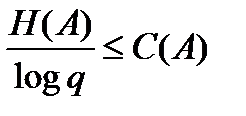В следующих выкладках все суммы берутся по i=1,..,n. Используется известное из математического анализа неравенство l n x   x – 1, log x  (x – 1) log e, а также неравенство Крафта (суммирование везде ведется от 1 до n).

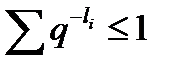( – по неравенству Крафта, ).

Для доказательства оценки сверху мы построим конкретный алгоритм алфавитного кодирования ϕ (известный как алгоритм Шеннона-Фано). Ведь если оценка сверху будет выполняться для некоторого C_ϕ(A), то она будет выполняться и для C(A).

В данном коде набор длин задается следующим соотношением.

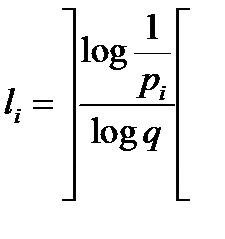(целая часть с избытком (сверху)).

Проверим, удовлетворяет ли этот набор неравенству Крафта.

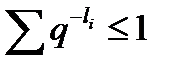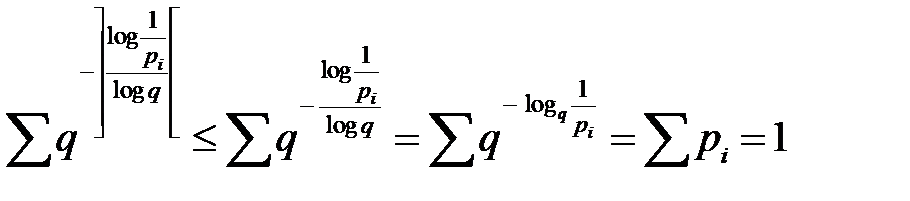
,  неравенство выполняется.

Теперь построим код точно также, как это делалось выше при доказательстве теоремы о существовании префиксного кода в случае выполнения неравенства Крафта (мы строили сначала слова B_i длины 1, затем слова длины два и т.д.).

 Оценим теперь сверху величину C_ϕ(A) для этого кода.

C_ϕ(A) = .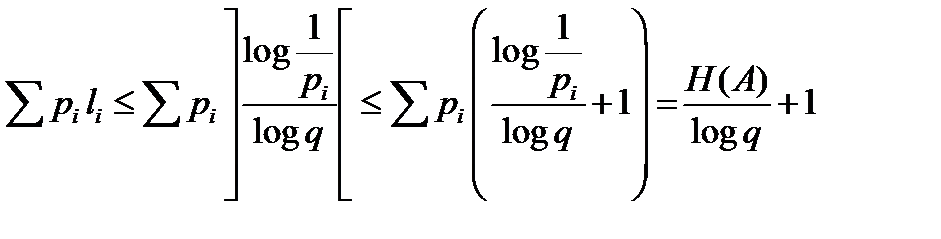

Теорема доказана.

В наших примерах часто будет использоваться двоичный алфавит. Очевидно, что для случая бинарного алфавита В получаем неравенство

Н (А)   С (А)   Н (А) + 1.

Предыдущая234567891011121314151617Следующая

Поделиться:

Воспользуйтесь поиском по сайту: