 |
Вероятностное доказательство второй теоремы Шеннона.
|
|
|
|
Это необязательное дополнение к лекциям для тех, кто уже знаком с самыми азами теории вероятностей. Базируется на лекциях [8].
Факты из теории вероятности.
Пусть  - случайная величина.
- случайная величина.  - мат. ожидание.
- мат. ожидание. 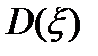 - дисперсия.
- дисперсия.
Теорема 13.3. (Неравенство Чебышева) Справедливо неравенство:
 .
.
Ошибки в канале моделируются испытаниями Бернулли, вероятность успеха p (неудача 1- p). Есть n испытаний. (Удачное испытание – произошла ошибка, неудачное – не произошла. Так как передается n символов, то мы получаем n испытаний во время передачи кодового слова.)
В случае источника Бернулли справедливы равенства: 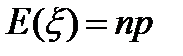 и D (ξ)= np (1- p).
и D (ξ)= np (1- p).
Первое из них очевидно, а ниже приведено краткое доказательство второго.
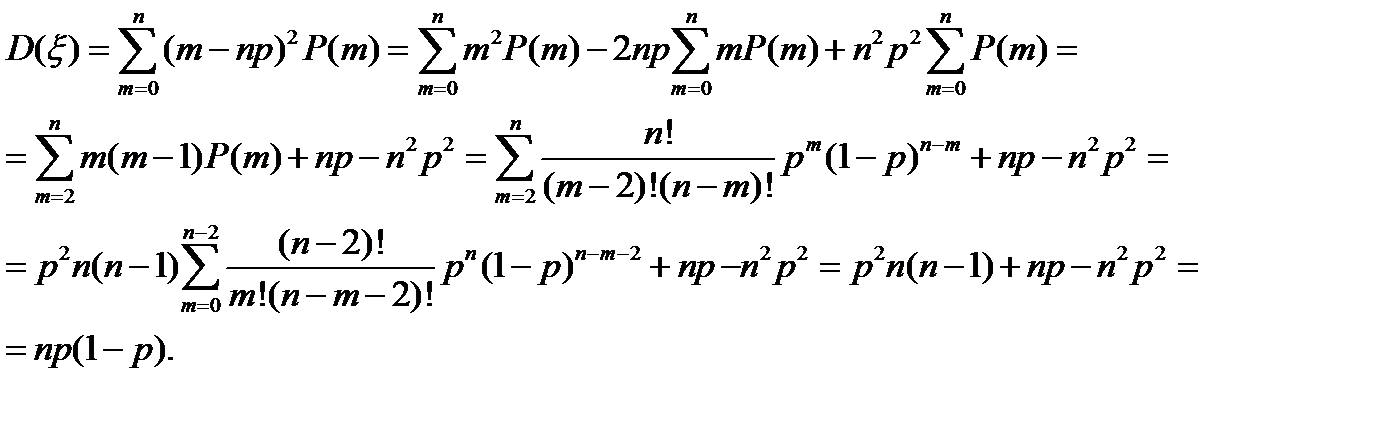
Пусть  - вектор ошибок. Он подчиняется распределению Бернулли, поэтому матожидание и дисперсия такого вектора
- вектор ошибок. Он подчиняется распределению Бернулли, поэтому матожидание и дисперсия такого вектора 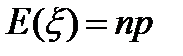 и D(ξ)= np(1- p).
и D(ξ)= np(1- p).
Рассмотрим некоторый код C = { x 1… xM }, где { x 1… xM }– кодовые слова (вектора Bn).
Применяем декодирование в ближайшее слово (по принципу наибольшего правдоподобия и согласно приведенной выше схеме декодирования, а,в случае нескольких вариантов, в кодовое слово с наименьшим номером). Обозначим через T(C) таблицу декодирования.
Пусть в канал передается вектор xi, а в декодер поступил вектор Y.
xi → канал → Y
Считаем, что Y = x i + e, где e – вектор ошибок.
Пусть τ – случайная величина, равная | e | (количество ошибок).
Т.к. так как относительно этой величины мы имеем распределение Бернулли, то E (τ) = np, D (τ) = np (1 – p).
Вводится некоторый параметр b =  , который носит чисто технический характер. Грубо говоря, если на одно слово приходится np ошибок, то мы будем окружать кодовые слова шарами радиуса ρ =[np+b], где b>0 – некоторая «маленькая» добавка
, который носит чисто технический характер. Грубо говоря, если на одно слово приходится np ошибок, то мы будем окружать кодовые слова шарами радиуса ρ =[np+b], где b>0 – некоторая «маленькая» добавка
|
|
|
Лемма 13.2. Справедливо соотношение
P { τ > ρ } ≤ ε \2
для любого заранее заданного ε.
Доказательство. Применим неравенство Чебышева:
P {| τ – E (τ)| > ε } ≤ D (τ)/ ε 2.
Положим ρ = [ E (τ) + b], тогда
P {| τ – np | > b} ≤ D (τ) / b 2.
Отсюда следует
P {| τ – np | > b } ≤ ε/ 2.
Тогда P (τ > ρ) = P {| τ – np | > b }. Это проиллюстрировано ниже:
- τ np τ
τ > nP + b
τ – nP > b
Отсюда следует P { τ > ρ }≤ P {| τ – np | > b}≤ D (τ) / b 2=ε/2.
Лемма доказана.
Лемма 13.3. Пусть ρ = [ E (τ) + b ] и b =  , тогда
, тогда
1\ n log | Sρ (x)| ≤ H(P) + O(n -1\2) при n → ∞.
Доказательство. Из леммы 13.1 и леммы 13.2 получаем неравенство:
| Sρ (x)| ≤ 2 nH (ρ \ n ).
Прологарифмируем и поделим на n, разложим логарифм в ряд (это корректно) и оставим главные члены:
1\ n log | Sρ (x)| ≤ H(ρ \ n) = - ρ \ n log ρ \ n – (1 – ρ \ n) log (1 – ρ \ n) = - [ nP + b ]\ n log [ nP + b ]\ n – (1 – [ nP + b ]\ n ] log (1 – [ nP + b ]\ n) ≈ - P log P – (1 – P) log (1 – P) + O(b \ n) = H(p)+ O(n -1\2).
Лемма доказана.
Введем некоторую функцию, определенную на парах векторов из Bn.
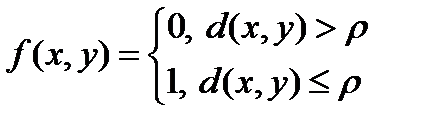 (13.5)
(13.5)
Лемма 13.4. Справедливо соотношение:
 (13.6)
(13.6)
Доказательство. Здесь P (xi) – вероятность неправильного декодирования переданного слова xi 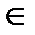 Bn. P (y| xi) - вероятность того, что при передаче слова xi на декодер попало слово y. Пусть Q(y| xi)- вероятность того, слово y декодировано в слово xi. Тогда
Bn. P (y| xi) - вероятность того, что при передаче слова xi на декодер попало слово y. Пусть Q(y| xi)- вероятность того, слово y декодировано в слово xi. Тогда

Заметим, что слово y может быть декодировано в слово xj, только если оно попало в шар соответствующего радиуса с центром в xj. Из этого следует, что

Если xi декодируется правильно, то y попало в шар нужного радиуса с центром в xi, и тогда 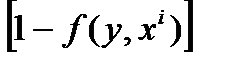 =0. В этом случае в неравенстве (13.6) слева 0, а справа неотрицательная величина. Если xi декодируется неправильно, то y попало в шар нужного радиуса с центром в xj, j≠i, и тогда, если
=0. В этом случае в неравенстве (13.6) слева 0, а справа неотрицательная величина. Если xi декодируется неправильно, то y попало в шар нужного радиуса с центром в xj, j≠i, и тогда, если 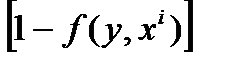 =0, то
=0, то

Если же 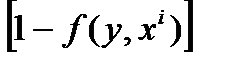 =1 (а это может быть, если шары пересекаются), то
=1 (а это может быть, если шары пересекаются), то
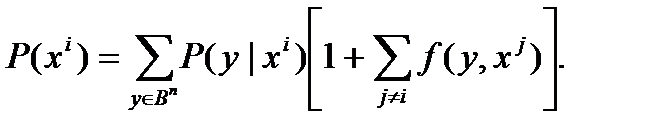
Лемма доказана.
Доказательство теоремы.
|
|
|
Теорема 13.4 (вторая теорема Шеннона). Для любого R: 0 < R < C (ρ), такого что M=2[nR], выполняется соотношение:
P *(M, n, P) → 0, n → ∞.
Доказательство. Пусть передаем x i, принято некое y, оцениваем ошибку декодирования.
Мы рассматриваем в качестве кодов все возможные подмножества Bn. Т.е. кодовые точки располагаются случайным образом. Точки упали как угодно, на них строим шары радиуса ρ.
Декодируем так: если точка у попала в шар радиуса t вокруг кодовой точки, то декодируем ее в данную кодовую точку, если в этом шаре нет других точек; если есть другие кодовые точки или у не попало ни в один из шаров вокруг кодовой точки, то у декодируем по эвристическим правилам. При этом возможна ошибка декодирования.
Вспомним введенную выше функцию f(x,y). Из леммы 13.4 следует, что вероятность того, что у находится от x i на расстоянии, большем ρ, задается формулой:

С другой стороны, из леммы 13.2 следует, что эта вероятность P { τ > ρ } ≤ ε \2.
Таким образом
Pc = 1\ M ∑ P (xi)= 


Заметим теперь, что E(f(y|xi)- математическое ожидание того, что у попал в шар с центром в x i, равно:
E(f(y|xi)=| Sρ (x)| / 2 n.
Теперь вспомним неравенство:
P *(M, n, p) ≤ 

Заметим теперь, что минимальное значение случайной величины не превосходит ее математического ожидания:
Minξ≤ E(ξ).
Из этих соотношений следует цепочка неравенств.
P *(M, n, p)  =
=
=  =
=  =
=
=  =
= 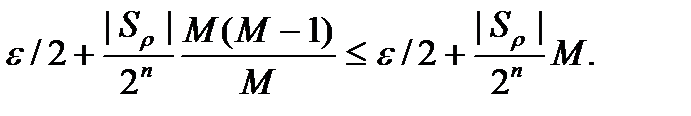
Таким образом
P *(M, n, p) – ε \2≤ 
Вспомним, что 0 < R < C (ρ), M=2[nR].
Применяем лемму 13.3 и соотношения: [nR] = log M, M = 2 Rn :
1\ n log (P *(M, n, P) – ε \2) ≤ 1\ n log (| Sρ | M \2 n)= 1\ n log | Sρ |2 Rn - n ≤ R – C (ρ) – 1+ O(n -1\2) + 1.
Пусть δ= C(P)-R. Тогда имеем при больших n неравенство
P *(M, n, P) < ε \2 + 2- δn.
Устремляем n→∞ и δ→0. Получаем
P *(M, n, P) →0.
Теорема доказана.
|
|
|


