 |
Тесты и матрица сравнений.
|
|
|
|
Определение. Множество 
-столбцов матрицы называется столбцовым покрытием для матрицы 
, если в подматрице 
, образованной столбцами из множества , нет нулевых строк. Длиной столбцового покрытия называется мощность множества , то есть 
.
Определение. Глубиной матрицы называется следующая величина:
(3.1)
Минимум в (3.1) берётся по множеству всех столбцовых покрытий матрицы .
Отметим следующее обстоятельство. Если 
— произвольная булева матрица, то под матрицей 
мы будем понимать матрицу, строками которой являются попарные суммы по mod 2 всех пар строк матрицы . Эта матрица называется матрицей сравнений. Смысл введённой операции состоит в следующем.
Утверждение. Пусть m≥2, тогда справедливо соотношение: 
,
где, как было введено выше, 
— глубина матрицы 
.
Доказательство. Индукция по m. Для случая m = 2
«Различимость» строк полностью определяется множеством единиц в сумме строк этой матрицы. Другими словами, «различимость» — это единицы в сумме, а ноль — это совпадение. Если эти две строки одинаковы, то в A нет никаких тестов, а в A 2 –столбцовых покрытий, т.е. 
.
Пусть утверждение справедливо для m строк и t (A)= k, т.е. подматрица, образованная столбцами i 1,…, ik, в A образует минимальный тест. Тогда эти же столбцы образуют в A 2 столцовое покрытие. В образованной ими подматрице не может быть нулевых строк, так как это бы означало, что в аналогичной подматрице матрицы A есть одинаковые строки. По этой же причине из минимальности длины теста следует минимальность мощности столбцового покрытия.
Добавим m +1 –ю строку. Если по-прежнему подматрица, образованная столбцами i 1,…, ik, в новой матрице A образует тест, то вновь эти же столбцы образуют в новой матрице A 2 столцовое покрытие. Заметим, что при добавлении строки длина теста не может уменьшиться. Поэтому и тест, и покрытие будут минимальными. Если же указанные столбцы уже теста не образуют, то они не образуют в A 2 и столбцового покрытия. Но тогда мы ищем в A минимальный тест, а рассуждениями, аналогичными приведенным выше, можно показать, что столбцы этого теста образуют в A 2 минимальное столбцовое покрытие.
|
|
|
Утверждение доказано.
Длина минимального теста для «почти всех» матриц.
Следующее вспомогательное утверждение, называемое неравенством Бернулли (неравенств с таким названием несколько!), бывает полезным в различного рода комбинаторных конструкциях.
Лемма (Бернулли). Пусть даны числа 
. Справедливо неравенство
Доказывается по индукции совсем просто.
В одном из приведенных выше примеров длина минимального теста равнялась m-1, а простая нижняя оценка это величины 
. А если взять матрицу случайно, то что может быть? Следующая теорема дает ответ на этот вопрос.
Теорема. Для почти всех 
-матриц длина максимального теста не превосходит 
.
Доказательство. Выделим некоторый набор столбцов 
и найдём число матриц , у которых эта совокупность является тестом.
Искомое число матриц равно следующей величине: 
.
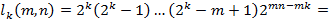
Тут использовалось неравенство Бернулли:
Здесь мы учли тот факт, что столбцы образуют тест, поэтому справедливо неравенство 
. Тогда, если 
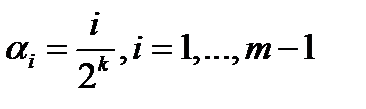, то выполняются условия применения этого неравенства 
.
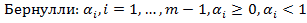Далее имеем
и при 
имеем
Таким образом,
при
Теорема доказана.
Упражнения.
Пусть 
- матрица из нулей и единиц.
1. Пусть строки матрицы Т(А) устроены так, что вместе с любой парой строк в матрице есть и строка, равная сумме этой пары по модулю два. Доказать, что в такой матрице любой тупиковый тест будет минимальным и
t(A)=log m.
2. Число тупиковых тестов таблицы не превосходит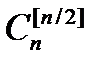 
.
|
|
|
3. Пусть строками матрицы являются все наборы с четным числом единиц. Найти t(A) и число тупиковых тестов.
4. Пусть строками матрицы являются все наборы с фиксированным числом единиц. Найти t(A) и число тупиковых тестов.
|
|
|
