 |
Частичный порядок — быть фрагментом.
|
|
|
|
Мы будем писать
если слово 
является фрагментом слова 
.
Пусть 
. Рассмотрим диаграмму Хассе следующего частичного порядка 
.
Общая геометрическая характеристика диаграммы Хассе частичного порядка 
состоит в следующем.
a) Если лежит в 
-м ярусе диаграммы Хассе, то есть 
, то степень исхода вершины равна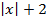 
.
b) Если слово имеет серий, то есть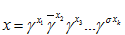 
где 
, то степень захода
вершины равна .
Другое качественное различие диаграмм Хассе частичных порядков, определённых выше, заключается в следующем обстоятельстве.
Предложение. Любая антицепь в Ч.У.М. имеет конечное число элементов.
Рассмотрим теперь следующее множество слов 
:
Предложение. Множество является антицепью в частично-упорядоченном множестве 
.
Таким образом, — это бесконечное множество слов, каждое из которых не является подсловом никакого другого слова из . Как было отмечено выше, такая ситуация невозможна в случае, когда частичный порядок задаётся отношением — «быть фрагментом».
Лекция 3. Признаковое кодирование. Тесты для таблиц.
Признаковое кодирование.
Метод признакового кодирования можно использовать в разных ситуация, но типичное его применение – кодирование «неформализованных» («нематематических») объектов.
| Субъект |
| Множество объектов |
| Код |
| s1 |
| sm |
| p1 |
| pk |
Признаки:
Рассматривается множество объектов s1,…,sm (люди, болезни, месторождения и т.п.), которое нужно кодировать, т.е. каждому объекту нужно сопоставить слово в алфавите. При этом есть другое множество объектов, называемых признаками, которые мы умеем кодировать. Тогда кодом объекта при признаковом кодировании является вектор, компонентами которого являются коды (значения) признаков, применительно к данному объекту.
|
|
|
При признаковом кодировании объекта 
признаком f называется отображение 
, где Df — множество допустимых значений признака.
Если заданы признаки f1,…,fn, то вектор x=(f1(x),…,fn(x)) называется признаковым описанием объекта x. Если признаковые описания отождествляют с самими объектами, то множество 
называют признаковым пространством.
В зависимости от вида множества признаки делятся на следующие типы:
1. бинарный признак: Df =(0,1);
2. номинальный признак: Df - конечное множество;
3. порядковый признак: Df - конечное упорядоченное множество;
4. количественный признак: Df - множество действительных чисел.
Можно использовать характеристические вектора признаков, например,
α (si) = (α 1, …, α k) 
.
Пример. s 1 … sn – люди.
Признаки:
1. Цвет волос
2. Рост
3. Вес
4. p 4 … pn – размеры частей тела человека.
Тесты для таблиц.
В случае бинарных значений признаков или использовании характеристических векторов при признаковом кодировании объектом исследования является матрица векторов признаков.
Определение. Тест - это множество столбцов в T (A) такое, что все строки в подматрице, образованной этим множеством, попарно различны.
Выше мы уже говорили о стремлении строить неизбыточные коды. С этой задачей связана известная проблема дискретной математики – проблема поиска минимальных тестов таблицы.
Длина теста – количество столбцов в тесте.
Тест минимальной длины для 
называется минимальным и его длина обозначается через 
. Тест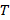 
называется тупиковым, если никакое подмножество 
тестом не является.
Когда таблица T (A) – это признаковая таблица множества объектов (строки таблицы – вектора признаков объектов), то длина теста указывает на количество признаков, которых достаточно для различения объектов. Эти признаки соответствуют столбцам теста. Но будет ли их достаточно, если количество объектов увеличиться? В связи с этим вопросом тестовая тематика возникает и при определении качества выбора множества признаков.
|
|
|
Конечно, как математический объект, тест – это скорее тема таких дисциплин как комбинаторика, дискретная математика, теория распознавания, но, так как он тесно связан с проблемой грамотного представления информации, то это объект и теории информации.
Для получения содержательных результатов в области построения минимальных тестов необходимо накладывать ограничение на вид и структуру векторов признаков. В качестве примеров приведем несколько утверждений, доказательство которых либо очевидно, либо является несложным. (Если не оговорено обратное – основание логарифма равно двум). T(A) – матрица из нулей и единиц.
|
|
|
