 |
Алгоритм на основе логического перманента.
|
|
|
|
Пусть  — логические функции от
— логические функции от 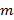 переменных и
переменных и  , где
, где  .
.
Определение. Логическим перманентом матрицы  называется следующая Д.Н.Ф.:
называется следующая Д.Н.Ф.:

где 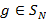 и
и  — симметрическая группа порядка
— симметрическая группа порядка 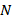 .
.
Таким образом, Д.Н.Ф. 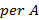 содержит
содержит  конъюнкций. Как обычно,
конъюнкций. Как обычно, 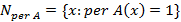 — это множество единиц логической функции
— это множество единиц логической функции 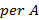 .
.
Пример. Пусть  ,
, 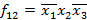 ,
, 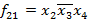 ,
, 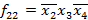 . Тогда
. Тогда
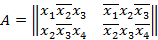
и
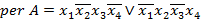
Далее
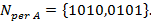
Пусть, как и ранее, 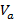 — класс эквивалентности, построенный по характеристическому множеству
— класс эквивалентности, построенный по характеристическому множеству 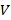 и содержащий слово
и содержащий слово  .
.
Конструкция 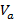 описывается следующими шагами.
описывается следующими шагами.
1) При заданном  и
и  находим слова
находим слова

2) Строим конъюнкции

При этом, если 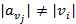 , то соответствующая конъюнкция — это тождественный нуль.
, то соответствующая конъюнкция — это тождественный нуль.
3) Строим матрицу 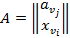 .
.
4) 
Обоснование пункта  довольно просто и состоит в следующем. Любое слово
довольно просто и состоит в следующем. Любое слово  обладает следующим характеристическим свойством. Всё мультимножество фраментов
обладает следующим характеристическим свойством. Всё мультимножество фраментов 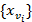 совпадает с мультимножеством
совпадает с мультимножеством 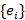 . Другими словами, для некоторой перестановки
. Другими словами, для некоторой перестановки 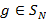 справедливы соотношения
справедливы соотношения

Решению системы соответствует решение уравнения
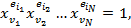 (9.4)
(9.4)
что соответствует элементу логического перманента матрицы  .
.
Пример. Пусть  ,
, 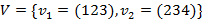 ,
, 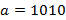 .
.
Применим к этому случаю алгоритм построения класса эквивалентности 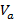 .
.
1)  ,
, 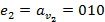 .
.
2) 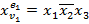 ,
, 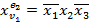 ,
, 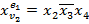 ,
,  .
.
3) 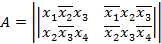 ,
,
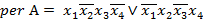
и 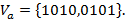
В общем виде матрица  имеет следующие параметры. Если
имеет следующие параметры. Если 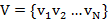 , то порядок
, то порядок  равен
равен 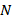 ; при
; при  ранг конъюнкции
ранг конъюнкции 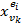 равен
равен  . Далее:
. Далее:  -я строка матрицы
-я строка матрицы  имеет вид:
имеет вид:  , а
, а  -ый столбец
-ый столбец

Пример. Если 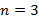 ,
,  и
и 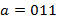 ,
,
то  ,
,  ,
, 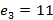 . Отсюда следует
. Отсюда следует
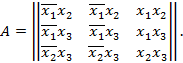
Разлагая 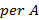 по первой строке, получаем выражение:
по первой строке, получаем выражение:
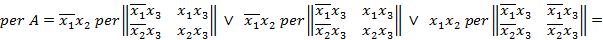
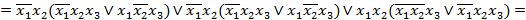
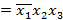
и, таким образом,  .
.
В общем виде Д.Н.Ф. 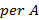 имеет
имеет  конъюнкций, максимальный ранг которых не превосходит
конъюнкций, максимальный ранг которых не превосходит 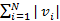 с учётом кратности вхождения букв и не превосходит
с учётом кратности вхождения букв и не превосходит 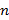 при классическом определении. Следует отметить также, что мы имеем дело не с «элементарными» конъюнкциями, а с некоторым их обобщением, представляющим специальный класс булевых функций, включающий в себя элементарные конъюнкции.
при классическом определении. Следует отметить также, что мы имеем дело не с «элементарными» конъюнкциями, а с некоторым их обобщением, представляющим специальный класс булевых функций, включающий в себя элементарные конъюнкции.
|
|
|
Следствие.  , где под нормой
, где под нормой 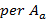 , понимается число единиц логической функции
, понимается число единиц логической функции 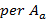 .
.
Следующий частный случай служит хорошей иллюстрацией для всех приведённых выше абстрактных построений.
Пусть 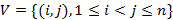 — характеристическое множество, которое соответствует всем парам букв
— характеристическое множество, которое соответствует всем парам букв  неизвестного слова
неизвестного слова  . Если
. Если 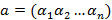 , то класс эквивалентности
, то класс эквивалентности 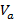 выглядит следующим образом — это логический перманент матрицы
выглядит следующим образом — это логический перманент матрицы  :
:

В частности, для  ,
,  матрица
матрица  имеет вид
имеет вид
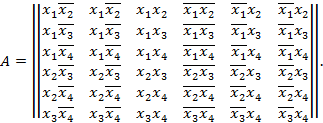
и
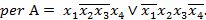
Конъюнкция 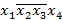 соответствует главной диагонали матрицы
соответствует главной диагонали матрицы  , а конъюнкция
, а конъюнкция  — второй главной диагонали этой матрицы. Ясно, что
— второй главной диагонали этой матрицы. Ясно, что 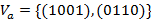 .
.
9.3 Пример на основе  -го слоя
-го слоя 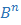 .
.
Одним из самых простых и естественных характеристических множеств является  -ый слой
-ый слой  или множество
или множество 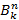
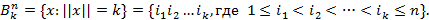
В содержательном смысле условие 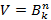 означает, что информацией о неизвестном слове
означает, что информацией о неизвестном слове  являются все его фрагменты длины
являются все его фрагменты длины  .
.
1) Пусть 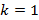 .
.
В этом случае
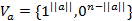
и каждый класс эквивалентности представляет собой слой куба  . Таким образом, имеется ровно
. Таким образом, имеется ровно  класс эквивалентности.
класс эквивалентности.
2)  .
.
В этом случае  и критерий эквивалентности двух слов
и критерий эквивалентности двух слов  и
и 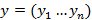 состоит в выполнении двух условий:
состоит в выполнении двух условий:
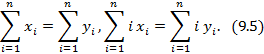
Условия (9.5) означают, что эквивалентные слова имеют одинаковый вес Хэмминга и одинаковую сумму номеров единичных координат. Для нахождения числа классов эквивалентности используем следующее утверждение.
Теперь заметим, что
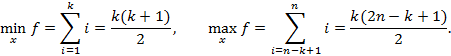
Предложение. Число классов эквивалентности для характеристического множества  равно
равно  .
.
С учётом предыдущих замечаний доказательство этого предложения состоит в нахождении разности 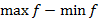 . Доказательство этого утверждения выносится в качестве упражнения. Это задача из задания.
. Доказательство этого утверждения выносится в качестве упражнения. Это задача из задания.
Пример. Для  разбиение на кассы эквивалентности имеет следующий вид:
разбиение на кассы эквивалентности имеет следующий вид:

Общее число классов эквивалентности равно 15.
Пример. Для 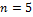 :
:

Общее число классов эквивалентности 26. Классы эквивалентности следующие:  .
.  ,
,  ,
, 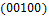 ,
, 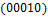 ,
,  .
. 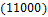 ,
, 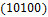 ,
, 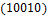 ,
,  ,
, 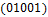 ,
, 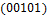 ,
,  .
. 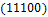 ,
, 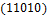 ,
, 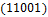 ,
, 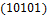 ,
, 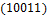 ,
, 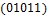 ,
, 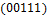 .
. 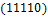 ,
, 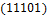 ,
, 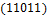 ,
, 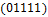 ,
, 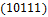 .
.  .
.
|
|
|
Для  биномиальные коэффициенты
биномиальные коэффициенты 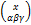 вычисляются следующим образом.
вычисляются следующим образом.
По определению
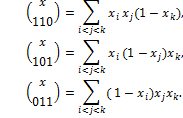
Так как
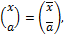
то приведённых выше формул достаточно для нахождения всех остальных биномиальных коэффициентов:  ,
,  ,
, 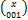 .
.
Далее
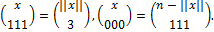
Подробные рутинные выкладки приводят к следующим полиномам, устанавливающим эквивалентность слов по характеристическому множеству  .
.
Пусть
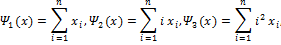
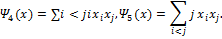
Если перейти в другую систему координат  , где
, где  — это номер
— это номер  -й единичной координаты в слове
-й единичной координаты в слове 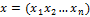 , то приведённые выше функции перейдут в следующие:
, то приведённые выше функции перейдут в следующие:
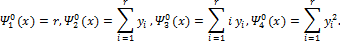
Предложение. Справедливо соотношение
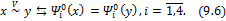
Таким образом, полиномы  ,
, 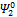 ,
, 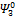 ,
, 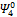 представляют собой полную систему инвариантов любого класса эквивалентности по характеристическому множеству
представляют собой полную систему инвариантов любого класса эквивалентности по характеристическому множеству  . Если при этом учесть число значений, которое принимает каждая из функций
. Если при этом учесть число значений, которое принимает каждая из функций 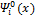 , а это, по порядку величины не превосходящие
, а это, по порядку величины не превосходящие 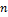 ,
,  ,
,  ,
,  , то можно получить оценку сверху для числа классов эквивалентности:
, то можно получить оценку сверху для числа классов эквивалентности: 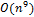 .
.
В общем виде система инвариантов строится следующим образом.
В соответствии со значениями биномиальных коэффициентов
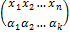
выписываются следующие полиномы:
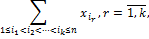
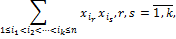

и так далее вплоть до
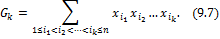
Всего полиномов вида (9.7) существует ровно 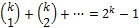 штук.
штук.
Упражнения.
1. Найти Va, если n=4, a=0101, V= {v1=(123), v2=(234)}.
2. Найти Va, если n=4, a=1101, V= {v1=(124), v2=(134)}.
3*. Доказать, что число классов эквивалентности для характеристического множества  равно
равно  .
.
|
|
|


