 |
Кодирование слов. О минимальной длине кода слова.
|
|
|
|
Пусть  и
и  . Под кодом слова
. Под кодом слова  мы будем понимать любое другое слово
мы будем понимать любое другое слово  , по которому слово
, по которому слово  можно восстановить однозначно. Например, если
можно восстановить однозначно. Например, если  — бинарное слово длины
— бинарное слово длины 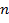 и
и  — номера единиц слова
— номера единиц слова  , то по слову
, то по слову  слово
слово  можно восстановить однозначно. Следующее определение связывает слова и слова.
можно восстановить однозначно. Следующее определение связывает слова и слова.
Определение. (А.Н. Колмогорова.) Пусть  — произвольная частично-рекурсивная функция (Машина Тьюринга). Тогда «сложность» слова
— произвольная частично-рекурсивная функция (Машина Тьюринга). Тогда «сложность» слова  по
по  есть следующая величина:
есть следующая величина:
 (4.3)
(4.3)
Любое слово  , удовлетворяющее условию (4.3), называется кодом или программой для слова
, удовлетворяющее условию (4.3), называется кодом или программой для слова  .
.
Таким образом, согласно (4.3), для восстановления «сложных» слов нужны длинные программы, а «простые» слова имеют короткие коды. Однако это определение включает в себя некоторый произвол, связанный с функцией  . Этот произвол состоит в том, что мы имеем дело с определённой машиной Тьюринга(Т-М). Таким образом, если
. Этот произвол состоит в том, что мы имеем дело с определённой машиной Тьюринга(Т-М). Таким образом, если  , то
, то  является кодом слова
является кодом слова  относительно Т-М, обозначаемой через
относительно Т-М, обозначаемой через  . Длина самого короткого кода обозначается через
. Длина самого короткого кода обозначается через  . Существование универсальной машины Тьюринга позволяет, в определённой степени, получить меру сложности, инвариантную относительно
. Существование универсальной машины Тьюринга позволяет, в определённой степени, получить меру сложности, инвариантную относительно  .
.
Теорема. Существует такая машина Тьюринга 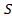 , что
, что

где константа  зависит лишь от МТ
зависит лишь от МТ  .
.
Казалось бы, что мера (4.3) позволяет адекватно и конструктивно оценивать алгоритмическую сложность кодирования произвольного слова. Однако это не совсем так, в силу следующего утверждения.
Теорема. Функция  , измеряющая сложность слова
, измеряющая сложность слова  относительно какой-нибудь универсальной машины Тьюринга, является алгоритмически неразрешимой.
относительно какой-нибудь универсальной машины Тьюринга, является алгоритмически неразрешимой.
Доказательство. Рассмотрим бинарный алфавит  и упорядочим все слова из
и упорядочим все слова из  сначала по длине, а потом по возрастанию (лексикографически).
сначала по длине, а потом по возрастанию (лексикографически).
|
|
|

Если существует Т-М  , которая вычисляет
, которая вычисляет  , то существует и Т-М
, то существует и Т-М  , которая «переводит» любое натуральное число
, которая «переводит» любое натуральное число  в первое по порядку (*) слово
в первое по порядку (*) слово  такое, что
такое, что  . Но тогда по числу
. Но тогда по числу  можно восстановить слово
можно восстановить слово  , то есть
, то есть  является кодом слова
является кодом слова  . Так как длина
. Так как длина  есть
есть  , то справедливо неравенство
, то справедливо неравенство  . Противоречие.
. Противоречие.
Замечание. Нетрудно понять, что существует лишь конечное число слов, сложность которых равна  . Действительно, если не так, то существуют слова, имеющие одинаковые коды, что противоречит условию однозначности кодирования.
. Действительно, если не так, то существуют слова, имеющие одинаковые коды, что противоречит условию однозначности кодирования.
Пусть  — конечное множество. Под кодированием
— конечное множество. Под кодированием  понимается любое инъективное отображение
понимается любое инъективное отображение  в некоторое множество бинарных слов. Другими словами, мы рассматриваем отображения вида
в некоторое множество бинарных слов. Другими словами, мы рассматриваем отображения вида  :
:

где  и
и  при
при  .
.
Длина кода  слова
слова  — это, по определению, длина слова
— это, по определению, длина слова  , то есть
, то есть  . Для того чтобы различать элементы множества
. Для того чтобы различать элементы множества  , коды этих элементов должны иметь определённые ограничения на длину. Точный смысл этого замечания состоит в следующем.
, коды этих элементов должны иметь определённые ограничения на длину. Точный смысл этого замечания состоит в следующем.
Лемма. Справедливы соотношения
1. 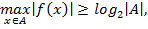
2. 
Доказательство. Так как число двоичных слов длины 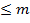 равно
равно

то если  , тогда для кодирования
, тогда для кодирования  имеется не более
имеется не более 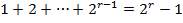 двоичных слов. Так как
двоичных слов. Так как  , то должно выполняться неравенство:
, то должно выполняться неравенство:  , что соответствует условию 1).
, что соответствует условию 1).
С другой стороны, словами длины  можно закодировать не более чем
можно закодировать не более чем  элементов множества
элементов множества  .
.
Лемма доказана.
Упражнения.
1. Найдите:
а) число бинарных слов длины n, имеющих ровно k серий;
б) число бинарных слов длины n, имеющих ровно k единичных серий;
в) число слов длины n над алфавитом  имеющих ровно k серий.
имеющих ровно k серий.
2. Пусть  – бинарное слово. Показать, что:
– бинарное слово. Показать, что:
а) число фрагментов вида (11) в слове a равно  , где
, где 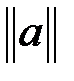 – число единиц в слове a;
– число единиц в слове a;
б) число фрагментов вида (01) в слове a равно 
3. Пусть  Слово
Слово  над алфавитом A называется монотонным, если
над алфавитом A называется монотонным, если  Найти число монотонных слов длины n над алфавитом A.
Найти число монотонных слов длины n над алфавитом A.
4. Пусть  – бинарное слово. Найти:
– бинарное слово. Найти:
а) общее число фрагментов слова  ;
;
|
|
|
б) число различных фрагментов слова 
5. Покажите, что
a) Число слов длины  , содержащих в качестве фрагмента данное слово
, содержащих в качестве фрагмента данное слово  длины
длины  , равно
, равно

b) Общее число подслов длины  в слове
в слове  равно
равно  .
.
c) Общее число фрагментов длины  в слове
в слове  равно
равно  .
.
|
|
|


