Префиксные кода и q-арные корневые деревья.

Итак, у нас есть два алфавита: А = (а ₁, …, а _n) и B = (b ₁, …, b_q).

Корневое дерево – это дерево, в котором полустепень захода корня равна нулю, а всех остальных вершин – единицы, а полустепень исхода любой вершины не превосходит q, называется q-арным корневым деревом.

Ребрам, исходящим из любой вершины можно сопоставить пометки: различные буквы из алфавита B. Любой вершине однозначно можно сопоставить слово: последовательность пометок ребер от корня к этой вершине. Висячие вершины (листья) – вершины с нулевой степенью исхода.

Легко доказать следующие два утверждения.

Утверждение. Любому префиксному коду можно сопоставить q-арное корневое дерево ровно с n листьями, которым в качестве пометок сопоставлены слова B₁, B₂,…, B_n.

Утверждение. Любому q-арному корневому дереву с n листьями, ребра и листья которого помечены по указанным выше правилам, соответствует побуквенный префиксный код, n букв которого закодированы словами – пометками листьев дерева.

5.5. Упражнения.

1. Найти El(156).

2.Найти Lev(324).

3. Найти набор натуральных чисел, если El(x)=0110000101100100100000010100100110.

4. Найти набор натуральных чисел, если Lev(x)=1110000111100001001111010001101.

5. Множество B бинарных слов называется префиксным, если никакое слово из B не является началом другого слова из этого же множества.

Пусть l_i  – слов длины i во множестве В. Доказать (не используя неравенство Крафта!) неравенство  

6.  Проверить неравенство Крафта и построить префиксный код при q=3 с длинами слов: 1,1,3,3,4,4.

Лекция 6. Метрические пространства и энтропийные конструкции.

Как уже говорилось выше, понятие информации не является математическим, но играет значительную роль не только внутри самой математики, но и во многих других областях знаний благодаря своему контексту и богатым коммуникационным возможностям. Эта ситуация отнюдь не является уникальной и такие понятия как «масса» или «энергия» тоже не имеют легитимного фундамента, что не мешает им играть ту роль, которая соответствует их интуитивному «физическому» смыслу.

Если считать, что информация всегда соотносится с некоторым объектом и как-то его характеризует, то понятие объекта тоже является первичным и первым его приближением является понятие множества в наивном смысле.

Если между элементами множества установлены какие-то связи, то мы получаем первые приближения к «реальным» объектам, которые характеризуются терминами граф, гиперграф и так далее. Измерение информации — это, в каком-то смысле, измерение расстояния между самим объектом и тем образом, который мы используем для его представления.

Информация по Хартли

Мощность множества является лишь одной из его характеристик. Однако в определённых ситуациях эта характеристика играет определяющую роль и все множества одинаковой мощности лежат в одном классе эквивалентности.

Определение. Пусть 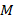 — конечное множество и 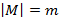. Тогда число  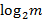называется энтропией множества .

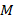Это определение тесно связано со способом задания конечного множества. Для того, чтобы задать 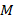, нужно найти способ или кодировку его элементов. Нет разницы между множеством  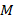и свойствами элементов 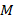. Если рассмотреть некоторое число предикатов 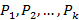, заданных на 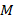, то для того, чтобы эти предикаты различали элементы  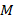необходимо выполнение условия: . Действительно, каждому элементу  поставим в соответствие двоичный набор , где 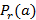 — значение предиката  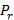на элементе . Число таких наборов будет  и потому для различения элементов 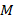 потребуется выполнение неравенства

Это условие имеет «информационный» характер и потому число 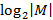 носит название информации или энтропии по Хартли конечного множества .

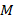Примеры

1) Рассмотрим все целые числа из интервала 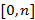. Каждое из них может быть представлено в двоичной системе счисления. Словом длины  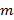из нулей и единиц, где . Таким образом, энтропия по Хартли этого множества равна .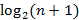
2) Пусть  — множество всех натуральных решений уравнения

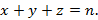
Раньше было показано, как можно найти 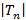 и доказывалось, что

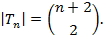
Таким образом, энтропия по Хартли множества  равна . Однако «описание» множества  является отдельной задачей и 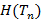 может служить лишь оценкой сложности такого описания.

Энтропийные «рассуждения»

Существует тип доказательных рассуждений в основе которых лежат энтропийные или, что то же самое, мощностные соображения. Вместо их описаний мы приведём несколько примеров.

Пример. Даны 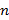 натуральных чисел 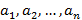. Показать, что из них можно составить сумму, делящуюся на .

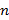Доказательство. Рассмотрим следующие суммы

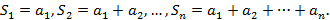
Так как число вычетов п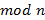о  равно 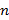, то либо какая-то из  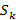делится на 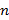, либо . Последнее означает, что сумма . Что и требовалось доказать.
Пример. В квадрат 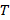 со стороной  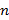брошена  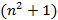точка. Доказать, что среди этих точек найдётся пара с расстоянием .

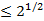Доказательство. Разобьём квадрат 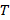 на 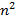 квадратов со стороной . Тогда хотя бы один из этих квадратов содержит 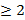 точек из брошенных. Расстояние между этими точками .
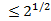Пример. Рассмотрим конъюнктивную нормальную форму (К.Н.Ф.) 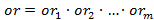, где

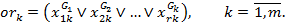
Проблема состоит в поиске  такой, что . Число «невыполняющих» наборов для 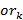 равно 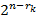, так как число решений уравнения

равно 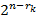. Поэтому общее число «невыполняющих» наборов для К.Н.Ф.  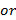не превосходит 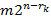. Отсюда вытекает следующее утверждение.

Утверждение. Если каждая скобка в 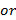 содержит больше, чем  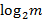букв, то К.Н.Ф.  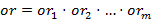выполнима.

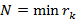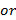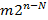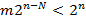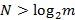Доказательство. Если , то число невыполняющих наборов для  не превосходит . Так как  при , то 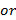 выполнима.

Замечание. Неравенство  является достаточным для выполнимости К.Н.Ф. Об «информационном» смысле этого неравенства речь будет идти ниже.

Пример. Следующее «энтропийное» рассуждение устанавливает бесконечность множества простых чисел путём «подсчёта возможностей».

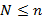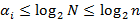Так как каждое натуральное число  имеет единственное представление в форме , где  и , то 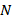 может быть «закодировано» набором длины  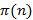натуральных чисел 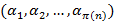, где 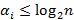. Число таких наборов не превосходит  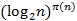и потому должно быть справедливо неравенство  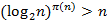и потому . Отсюда следует, что .

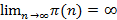Что и требовалось доказать.

6.3 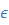-сети.

Хотя понятие энтропии по Хартли было введено только для конечных множеств, существуют математические конструкции, которые позволяют распространить это определение для бесконечных множеств, обладающих определённой структурой, дающей возможность «аппроксимировать» элементы этих множеств с помощью понятия расстояния.

 Ключевым понятием при этом является понятие 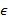-сети, и энтропия по Хартли — это энтропия этой 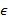-сети, которая является конечным множеством при определённых ограничениях на исходное бесконечное множество.
Пусть 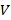 — некоторое метрическое пространство с метрико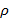й  и 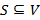. Тогда пара  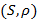называется метрическим множеством.

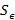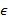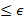Определение. Множество  называется -сетью для , если любой элемент из  лежит в шаре радиуса  с центром в некоторой точке .

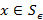Если минимальная мощность 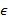-сети равна 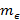, то величина  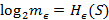называется 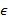- энтропией множества . В определённом смысле 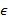-энтропия характеризует «сходство» элементов множества .

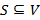Следующее определение связано с понятием различимость.

Определение. Множество 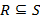 называется, если 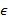- различимым

для .

Рассмотрим все 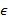-различимые множества в  и через 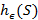 обозначим энтропию максимального по мощности 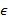-различимого множества в . Следующие простые неравенства связывают 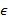-энтропию и или .

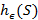Утверждение. Для всякого ограниченного и замкнутого множества 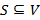 справедливы неравенства

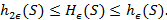(6.1)

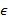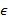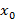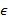Доказательство. Если  — максимальное по мощности -различимое множество, то шары радиуса  с центром в  покрывают . Действительно, если точка  не покрыта, то  для всех  из . Но тогда множество  — это -различимое множество, что противоречит определению . Отсюда следует верхняя граница

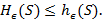
С другой стороны, в каждом шаре радиуса 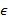 не может быть более одной точки из 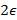-различимого множества. Справедливо неравенство

Что и завершает доказательство сформулированного утверждения.

Использование неравенств (6.1) является стандартным приёмом при оценке 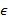-энтропии метрических пространств. Ниже приведено несколько примеров таких вычислений.

Пример. Пусть  — 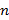-мерное пространство над полем вещественных чисел с метрикой Эвклида и  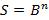— единичный 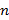-мерный куб

Найдём 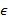-энтропию множества .

Рассмотрим следующую решётку в

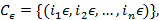
где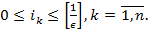

Мощность решётки  равна 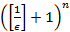 и для 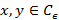 справедлива оценка

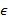Таким образом,  — это -различимое множество в , имеющее энтропию

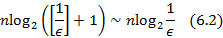
при 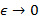. Отсюда получаем оценку

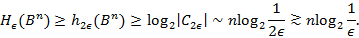
Пусть теперь 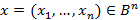. «Приблизим» точку  следующей точкой решётки , где

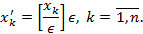
Имеем, по определению,

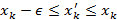
и отсюда следует оценка

(6.3)

Из неравенства (6.3) следует, что точки решётки  образуют 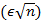-сеть в . Отсюда и из (6.1) получаем оценку

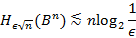
и потому

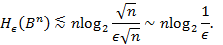
Отсюда вытекает

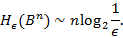
Пример. В качестве второго примера обратимся к вычислению 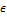-энтропии множества дифференцируемых функций с ограниченной производной, заданных на отрезке 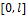. Это множество мы обозначим через 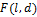, где

при .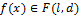

Разобьём отрезок 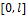 на интервалы длины . Число точек в полученной решётке равно 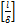. Рассмотрим разложение функции  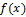в ряд Тейлора в точке решётки :

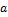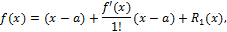
где  — остаточный член в какой-нибудь классической форме. Мы используем известную оценку

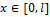где . Для нашего случая  и 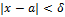. Поэтому

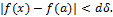
Если положить , то получим неравенство

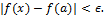
Число точек решётки при таком выборе параметров равно 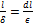 и потому

Более общим утверждением типа сформулированного выше является следующая теорема А.Н. Колмогорова.

Пусть 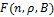 — множество функций от 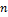-переменных, имеющих частные производные до порядка  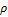включительно, где 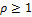, ограниченные сверху константой 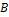. Если это множество снабдить чебышевской метрикой

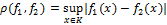
при  и обозначить через  его 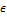-энтропию, то имеет место следующее утверждение.

Теорема А.Н. Колмогорова. Справедлива асимптотическое соотношение

где 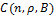 — константа, не зависящая от .

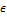Стандартная интерпретация соотношения (7.6) следующая: сложность класса функций 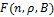 разумно измерять величиной отношения . Последнее, в частности, означает следующее: если , то существуют функции из класса 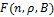, не представимые в виде суперпозиции функций из класса .

Предыдущая12345678910111213141516Следующая

Поделиться:

Воспользуйтесь поиском по сайту: