 |
Лекция 7. Свойства энтропии по Шеннону. Алгоритмы сжатия информации.
|
|
|
|
Свойства энтропии.
Здесь в качестве справки мы приведем некоторые свойства энтропии по Шеннону. Это даст вам возможность лучше понять смысл этого понятия и сферу его практического применения. Для дальнейшего изложения нам понадобятся только свойства 5 и 6. Они очевидны из определения энтропии и простейших комбинаторных соотношений, известных вам и могут быть никак не связаны с Теорией вероятностей. В качестве их следствия получается свойство 7. Остальные утверждения приводятся для тех, кто знаком с самыми азами этой теории.
Случайный источник можно трактовать как событие с множеством исходов, вероятности которых заданы.
Рассмотрим два события X и Y. Исходы первого события будем обозначать через x, а второго - через y. Введем по определению понятие условной энтропии H(X/y).
H (X| y) = 
.
Это случайная величина. А теперь усредним H (X| y) по всему множеству Y и получим уже неслучайную величину H (X| Y).
Перейдем теперь к перечислению свойств. В некоторых случаях приводятся доказательства.
1) H (X) 
0.
2) H (X) является выпуклой вверх функцией своих аргументов функция своих аргументов p 1 … pn.
3) H (X) 
log|X| (если все события равновероятны, то энтропия максимальна).
4) H (X| Y) H (X) (Аналог свойства 3 для условной энтропии. Дополнительная
информация не увеличивает энтропию).
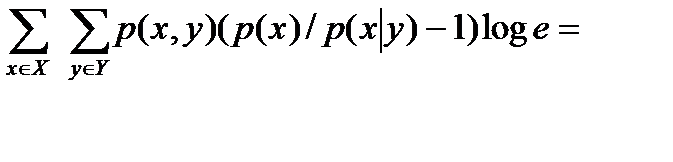
5) Пусть Х и Y – независимые события. Справедливо равенство
H (XY) = H (X) + H (Y).
6) Пусть два события имеют равное число исходов, а вероятности этих исходов как множества совпадают, т.е. они состоят из одних и тех же (p 1,…, pn), но в разном порядке. Справедливо равенство
H (X) = H (X ’).
7) Пусть есть событие Х = (p 1,…, pn) и некоторое подмножество его исходов А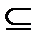 
(p 1,…, pn). Построим новое событие ХА таким образом, что его исходы задаются вероятностями 
(«сглаживание» фрагмента).
|
|
|
Справедливо неравенство
H (х) H (ХА).
Доказательство. Доказательство следует из свойств следует из (2) и (6).
По свойству (2) энтропия выпуклая вверх функция своих аргументов, а для такой функции f выполняется неравенство Йенсена 
.(Здесь числа α 1 … αn, αi> 0, 
.)
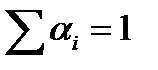Без ограничения общности считаем, что первые m элементов Х образуют подмножество А, т.е. исходы X задаются вероятностями p 1 … pmpm+ 1 … pn
Строим вспомогательные события:
X 1 = X
X 2 = p 2 p3… pmp 1 pm+ 1 … pn
X3 = p3 p4… p 1 p 2 pm+ 1 … pn
Xm = pmp 1 … pm- 2 pm- 1 pm+ 1 … pn
Из свойства (6) следует, что H (X) = H (X1) = … = H (X m) (все события состоит из одинаковых множеств значений вероятностей). Тогда можно ХА представить в виде (H (X) + H (X1)+ … + H (X m))/m. Применяем неравенство Йенсена, где все αi=1/ m. Получаем H(ХА)≥ (H (X) + H (X1)+ … + H (X m))/m. Отсюда следуетH(ХА)≥H(A).
8) H (XY) = H (X) + H (Y|X) = H (Y) + H (X|Y).
Следует из известных в теории вероятностей соотношений: P (XY) = P (X) 
P (Y | X) и P (XY) = P (Y) P (X| Y).
9) H (X 1 X 2 … Xn) = H (X 1) + H (X 2 | X 1) + H (X3| X 1 X 2) + … + H (Xn| X 1 X 2 … Xn- 1).
Следует из известных в теории вероятностей соотношения: P (X 1 … Xn) = P (X 1) P (X 2| X 1) … P(Xn|X1,…,Xn-1).
10) H (X|YZ) H (X|Y).
Доказывается по аналогии с доказательством свойства (4).
11) Пустьзадано событие X и на множестве его исходов определена функция y = g (x). Введем событие Y с множеством исходов y = g (x). Тогда H (Y) H (X). Равенство H (Y) = H (X) достигается тогда и только тогда, когда существует обратная функция
g – 1.
Доказательство. Следует из свойства (8).
H (X) + H (Y| X) = H (Y) + H (X| Y) 
H (Y) = H (X) + H (Y| X) – H (X| Y) 
0.
Т.к. у полностью определяется по х, то H (Y| X) = 0.
Алгоритмы кодирования
Алгоритм Шеннона (Фано).
Передаваемые символы располагаются в порядке убывания (или возрастания) вероятностей. Построим таблицу, первым столбцом которой являются идентификаторы передаваемых символов. Назовем, например, верхней частью этой получившейся последовательности символов ту, которая начинается минимального номера. Эта упорядоченная последовательность фиксируется, затем идут шаги алгоритма.
|
|
|
Каждый шаг – это горизонтальное деление на q частей этой последовательности, а i-й шаг – деление одной из выбранных на предыдущем этапе частей. Рассмотрим частный случай бинарного алфавита. В этой ситуации деление происходит на две части.
Деление происходит так, чтобы в каждой половине суммы вероятностей отличались бы на минимально возможную величину (при нескольких вариантах берется, например, с избытком часть с наименьшими номерами букв).
Затем каждое деление порождает символ алфавита B, который приписывается при таком делении к коду верхней части добавляется 0, а нижней – 1.
Так происходит до тех пор, пока в каждой из получившихся частей не останется по одному элементу. Тогда приписанные части последовательности нулей и единиц и будут кодами этих элементов.
Пример.
Нужно передавать семь букв. Их вероятности заданы. Схема алгоритма приведена ниже.
Таким образом полученные коды букв такие:
a 1 – 00, a 2 – 01, a 3 -100, a 4 -101, a 5 -110, a 6 -1110, a 7 -1111.
Стоимость кодирования 2,625. Энтропия:
H = 1/4 log 4 + 1/4 log 4 + 1/8 log 8 + 1/8 log 8 + 1/8 log 8 + 2 * 1/16 log 16 = 2, 25
Пример.
Стоимость кодирования 2,28.
H = 7/18 log 18/7 + 1/2 log 6 + 1/5 log 9 = 2,17
Алгоритм Хаффмана
Алгоритм дает результат не хуже, чем метод Шеннон-Фано. Более того, можно показать, что стоимость кодирования этим алгоритмом равна C(A).
Для случая двоичного кодирования код строится при помощи бинарного корневного дерева. (В случае произвольного q используется q-арное дерево). Из каждой вершины выходит два ребра: правое помечаем 1, левое – 0. Листья такого дерева кодируются последовательностью пометок от корня к листу. Очевидно, что множество соответствующих этим листьям слов образует префиксный код.
Вначале мы строим вершины дерева (листья), соответствующие передаваемым буквам. Они помечаются значениями вероятностей. Затем на каждом шаге берутся две вершины с наименьшими пометками. Они образуют родительский узел, пометка которого равна сумме пометок вершин, и исключаются из дальнейшего рассмотрения. Шаги продолжаются до появления корня.
Пример.
|
|
|
Рассмотрим тот же пример, что и для кода Шеннона-Фано.
Итерации о построение листьев бинарного дерева.
(1, 2, 3, 4, 5, 6, 7) → (1, 2, 3, 4, 5, (6, 7)) → (1, 2, (3, 4), 5, (6, 7)) → (1, 2, (3, 4), (5, 6, 7)) → ((1, 2), (3, 4), (5, 6, 7)) → ((1, 2), (3, 4, 5, 6, 7))
Теперь, начиная с корня, строим пометки ребер дерева:
| (6,7) |
| (5,6,7) |
| 7 |
| 6 |
| (3,4) |
| (3,4,5,6,7) |
| 5 |
| 1 |
| 4 |
| 3 |
| 1 |
| (1,2) |
| 2 |
| 0 |
Получаем код. a 1 – 00, a 2 – 01, a 3 -100, a 4 -101, a 5 -110, a 6 -1110, a 7 -1111.
Стоимость кодирования 2,625.
|
|
|
