 |
Дополнительная информация влечет дополнительную неопределенность.
|
|
|
|
Обратимся опять к исходной модели распознавания слов по фрагментам при заданном характеристическом множестве 
. Информация, полученная о слове 
при помощи множества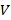 
, — это мультимножество фрагментов 
. Если мы «расширим» характеристическое множество, то есть рассмотрим множество 
такое, что 
, то информацией о слове 
будет являться мультимножество фрагментов, содержащее исходное мультимножество . Что при этом произойдёт с классами эквивалентности, порождёнными множеством 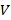? Интуитивно очевидный ответ, состоящий в том, что классы эквивалентности не «расширятся», оказывается неверным. Рассмотрим следующий пример.
Пусть 
и 
. Для любого слова 
имеем
Отсюда получаем:
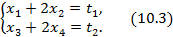
При любых натуральных 
и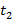 
система (10.3) имеет единственное 
решение. Отсюда следует, что характеристическое множество 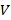является полным, то есть каждый класс эквивалентности содержит ровно одно слово.
Рассмотрим теперь «расширенное» характеристическое множество 
. Если 
, то класс эквивалентности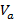 
определяется таким мультимножеством фрагментов: 
. Далее, если 
, то 
и потому 
. Таким образом, класс эквивалентности 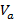содержит более одного элемента и множество не является полным.
Объяснить эту ситуацию можно следующим образом. Каждый фрагмент слова несёт определённую информацию об этом слове. Но с этим же фрагментом связана и неопределённость, которая заключается в том, что неизвестно от «действия» каких элементов характеристического множества получился этот фрагмент. Потому «увеличивая» мощность характеристического множества мы, с одной стороны, поднимаем уровень информированности о неизвестном слове, а с другой стороны повышаем степень неопределённости о способе получения этой информации. От исхода такого рода коллизий и возникают эффекты типа отмеченного выше.
|
|
|
Полные характеристические множества.
Возвращаясь ко всему сказанному выше напомним, что информацию о неизвестном слове мы получали в виде фрагментов этого слова, которые, в свою очередь, формировались с помощью характеристического множества 
. Возникает естественный вопрос о «структурных» свойствах множества 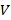, которые влияют на количество информации, получаемой о неизвестном слове.
Определение. Характеристическое множество 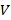называется полным, если 
для любого слова 
.
Тривиальным примером полного характеристического множества является 
. Если 
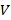, то множество также является полным при 
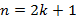. Этот пример может быть обобщён следующим образом.
Если представление
есть разбиение и 
для 
, то характеристическое множество 
является полным.
Пример. Рассмотрим следующее характеристическое множество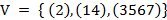 
. Если 
, то фрагменты следующие: 
. Восстановление по этому множеству фрагментов производится очевидным образом: 
.
Отметим теперь, что множество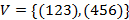 
при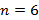 
не является полным, так как
и, в общей форме, множество 
также не является полным. Таким образом, разница между полными и неполными характеристическими множествами может быть незначительной.
Если 
, то следующая конструкция даёт нижнюю границу для 
, при котором 
является полным множеством. Эту границу мы обозначим через 
.
Теорема 10.3. Справедливо соотношение 
Доказательство этого неравенства – сложная задача и не входит в нашу программу. Ниже приводятся некоторые соображения на эту тему и схема доказательства.
Схема доказательства.
Заметим, что слова 
и 
«неразличимы» по фрагментам длины 
или формально
Далее
Действительно, по критерию (9.5)
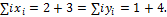
Итерируя эту процедуру, получаем
Так как длина слова 
, то из следует, что
|
|
|
Дополнения и замечания.
Отметим также, что каждое характеристическое множество 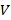порождает разбиение 
и энтропия такого разбиения равна следующей величине
Мощность каждого класса эквивалентности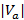 
может быть найдена как число единиц логического перманента булевой матрицы, построенной по характеристическому множеству 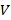. Такого рода вычисления были приведены выше.
Рассмотрим теперь следующую задачу. Дано некоторое множество слов 
, каждое из которых имеет длину , то есть 
. Существует ли слово 
длины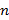 
такое, что 
Другими словами, существует ли слово длины 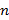такое, что каждое из слов 
является фрагментом ? Таким образом, в этой задаче три параметра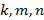 
и ответ, очевидно, зависит от их соотношений.
1) Если 
, то ответ положительный для любого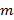 
. Действительно, слово 
содержит в качестве фрагмента любое слово длины .
2) Если 
, то ответ в общем виде негативный уже для 
, так как при 
, 
никакое слово длины 
не содержит 
и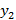 
в качестве фрагментов.
Таким образом, неопределённым остаётся случай 
и 
— некоторое произвольное множество из 
. То есть для некоторого множества слов , каждое из которых имеет длину , описать критерий существования слова длины 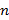такого, что
Довольно просто решается также следующая задача распознавания: даны два слова 
и , является ли фрагментом ? Если 
, 
, то решение этой задачи выглядит следующим образом.
1) Выбираем число 
, исходя из условия
Если не существует, то ответ в исходной задаче: нет. Если существует, то переходим к шагу 
.
2) Рассмотрим слова 
, 
как новые входные данные и переходим к шагу 
.
Имеется довольно тесная и естественная связь между характеристическими множествами 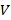и булевыми полиномами. Действительно, каждому булеву полиному
можно сопоставить характеристическое множество 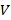по следующему правилу: если 
, то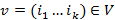 
.
Обратное соответствие осуществляется очевидным способом: если 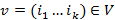, то 
является мономом полинома 
.
В терминах понятия 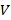-эквивалентности эта связь имеет следующее выражение.
Предложение. Если 
, то 
.
Доказательство. По определению
По условию 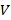-эквивалентности мультимножество 
однозначно определяется мультимножеством 
, что и приводит к равенству .
Упражнения.
1. Используя теорему о количестве вхождений одного слова в другое как фрагмента перевести сериальный код 0312010 в последовательность номеров единичных позиций.
|
|
|
2**. Превратить схему доказательства теоремы 10.2 в строгое доказательство.
3***. Превратить схему доказательства теоремы 10.3 в строгое доказательство.
|
|
|
