Лекции 14. Линейные коды: спектры, двойственность.

Линейные коды.

Наложим на множество C  ограничение, превратим его из подмножества в  подпространство Bⁿ.

 Это даст возможность использовать результаты линейной алгебры.

Определение. Код C Bⁿ называется  линейным (групповым), если для любых α, β C: α + β C.

Сразу из определения следует, что групповому коду обязательно принадлежит нулевой вектор.

Заметим, что если код не является двоичным, то понятия линейного и групповых кодов не совпадают.

В случае двоичного кода: Bⁿ – линейное пространство; зададим в нем подмножество векторов C Bⁿ, и для любых α, β C: α + β C. Отсюда следует, что вместе с любым набором вектров линейному коду принадлежит их линейная комбинация, поэтому C – подпространство Bⁿ.

Пусть dimC = k, | C | = 2 ^k. Согласно определению: C – групповой код.

Легко показать, что d (c) = min | α | (α С, α 0).

Для любого линейного кода существуют 2 матрицы: G – порождающая, H – проверочная.

                  

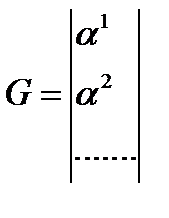
Порождающая матрица состоит из векторов (записанных в строке покомпонентно) некоторого базиса подпространства C. Для любого β C: β – линейная комбинация строк G. Если dimC = k, то G должна содержать k строк.

Проверочная матрица кода C – это такая матрица, что для любого α С:

α H^T = 0.

При построении кода (алгоритмов кодирования и декодирования) C чаще используется матрица H.

Определение. Код С* Bⁿ называется ортогональным C, если для любых α, β: α С*, β С выполняется условие: αβ = 0.

Из курса линейной алгебры известно, что если dimC = k, то dimC* = n – k. При этом порождающей матрицей H * кода С*  является проверочная матрица H кода С. (И наоборот.)

Пример. Код с проверкой на четность.

dimC = n – 1, dimH = 1, H = (11…1)_{1x n}

Рассмотрим теперь операции преобразования кодовых матриц.

Элементарные преобразования матриц:

1) Перемена местами строк.

2) Умножение строки на число.

3) Сложение строки с линейной комбинацией других строк.

4) Перемена столбцов местами.

Определение. Коды C и D называются эквивалентными, если G (C) можно получить из G (D) с помощью элементарных преобразований.

Утверждение. Для любого С существует эквивалентный код С’ такой, что

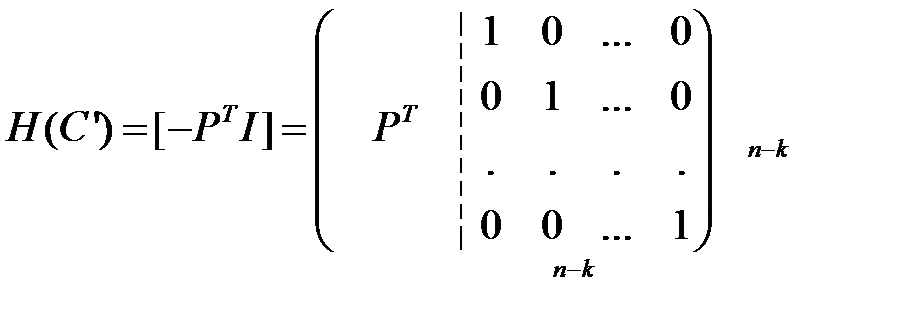  (14.1)

Определение. Код с порождающей матрицей вида (14.1) называется систематическим.

В таком коде в подматрице  находятся информационные столбцы, в  - проверочные столбцы.

Проверочных символов (n – k). В H (C’) (n – k) строк, каждая строка – соотношение, задающее линейную комбинацию: 1-я – 10…0, 2-я – 01…0 и т.д.

Пример.

n = 5, k = 3 и

           

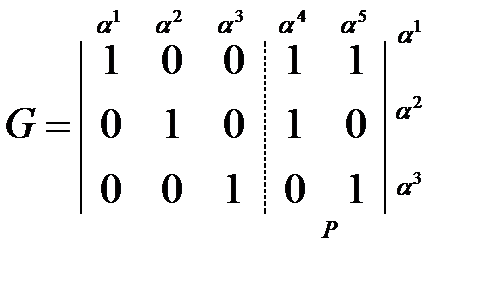
Пусть α ₁, α ₂, α ₃ – информационные символы, α ₄, α ₅ – проверочные. Тогда проверочные соотношения:

Алгоритм кодирования осуществляется следующим образом: любая строка H дает проверочную комбинацию. Так мы преобразуем слова из B^k, подлежащие передаче, просто добавляя к ним n-k символов – результаты проверочных соотношений после подстановки туда информационных символов.

  Заметим, что в нашем примере мы получили код с d (C) = 2.

В общем случае для декодирования с помощью таблицы декодирования на декодере хранится и в процессе алгоритма декодирования обрабатывается таблица, содержащая  n2ⁿ символов (2ⁿ векторов). Вы уже знаете, насколько сложно работать с экспоненциальным объемом информации.

Свойство линейности кода позволяет в этом вопросе получить существенную выгоду. Для хранения таблица декодирования нужно хранить ее первую строку и первый столбец, т.е. 2^n-k+2^k векторов. Это следует из того, что линейный код B^k – это подгруппа абелевой группы Bⁿ.

 Раскладывая группу по подгруппе мы получаем таблицу декодирования в виде матрицы, первая строка которой, как обычно, векторы кода, а остальные – смежные класс. Тогда первый столбец – это образующие смежных классов.

Для линейных кодов такой алгоритм декодирования  называется декодированием с помощью «стандартной расстановки».

Определение. Синдром линейного кода  называется вектор S_α = α H^T.

Если проверочная матрица имеет (n — k) строк, то синдром S_y произвольного вектора у  из B ⁿ является вектором длины (n — k).

Поскольку по определению линейного кода вектор у является кодовым тогда и только тогда, когда yH^T = 0, то справедливо следующее утверждение.

Утверждение. Синдром S_y вектора у равен 0 тогда и только тогда, когда у является кодовым вектором.

Утверждение. Для двоичного линейного кода синдром S_y принятого вектора у равен сумме тех столбцов проверочной матрицы H, где произошли ошибки.

Утверждение. Пусть U – кодовое слово,при передаче из него получено слово V= U + e, где вектор e – вектор ошибки. Алгоритм на основе стандартной расстановки правильно декодирует слово тогда и только тогда, когда вектор ошибки – образующая смежного класса.

Оно вытекает из следующего утверждения.

Утверждение. Два вектора u и v принадлежат одному и тому же смеж­ному классу тогда и только тогда, когда их синдромы равны.

Достаточно важным для линейных кодов является следующее простое утверждение.

Теорема 14.1.     Кодовое расстояние линейного кода d (C) = d, тогда и только тогда, когда любые (d – 1) столбцов H линейно-независимы и данное d является максимально возможным.

Спектр кода.

Существует еще одна важная характеристика кода – это спектр кода.

Рассмотрим код V = (v ₁… v_k). Пусть для кодового слова v_i величина r_s (v_i) – это число кодовых слов таких, что ρ (v_j, v_i) = s. Тогда вектору v_i сопоставляется (r ₀(v_i)… r_k (v_i)) – спектр v_i – кода. А спектры всех кодовых точек можно задавать в виде таблицы размером (k+1)xk.

Если V – линейный код, то спектры всех v_i одинаковые. Поэтому для линейного кода спектром называется вектор (a ₀… a_n), т.е. число кодовых слов весов 0… n.

Важным инструментом использования спектра является теорема Маквильямс.

Теорема 14.2. (Маквильямс).

Пусть есть код V и его спектр (a ₀… a_n) и код ортогональный V * и его спектр (b ₀… b_n), тогда справедливо соотношение , где z – переменная.

Мы здесь даем саму теорему без доказательства.

Эта теорема дает возможность выражать спектр кода через спектр ортогонального кода.

Оно имеет несколько важных следствий, применяющихся не только в теории кодирования, но в комбинаторике. Приведем некоторые из них.

Следствие1. Пусть 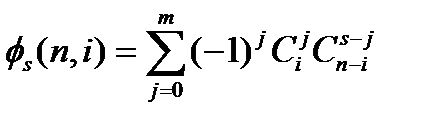. Тогда справедливо соотношение

.

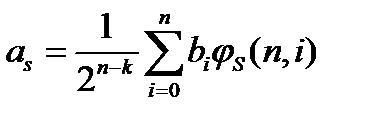Доказательство. Так как 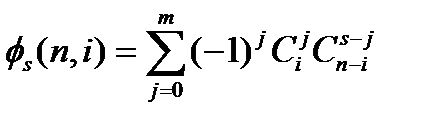, то из

с использованием теоремы Маквильмс получаем

.

Приравнивая коэффициенты при одинаковых степенях, имеем

.

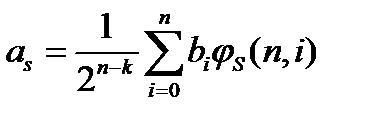Следствие доказано.

Заметим, что из 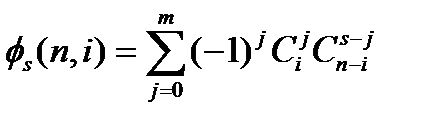 следует, что

.

Следствие 2. Справедливо соотношение

, где 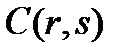 - число точек B_n веса s на расстоянии r от некоторой точки кода.

Пусть C (s) – число точек Bⁿ веса s, попавших в шар радиуса t линейного кода, исправляющего t ошибок.

Следствие 3. Справедливо соотношение:

.

Ниже мы приведем пример использования этих соотношений.

Упражнения.

1. Пусть G – произвольный -код, точки которого выписаны в матрицу A размером . Показать, что каждый ненулевой столбец A содержит ровно  единиц.

2. Пусть G – произвольный -код. Доказать следующие неравенства:

a) ;

b) .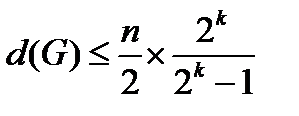

3.Доказать следующие «общие» свойства функции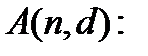

4*.Доказать, что при n≥2d-1 число проверочных символов, необходимое для того, чтобы минимальный вес линейного кода с n символами достигал значения d, равно, самое меньшее, 2d- log d-2.

Предыдущая45678910111213141516171819Следующая

Поделиться:

Воспользуйтесь поиском по сайту: