Лекция 15. Дополнения. Примеры.

Код Хэмминга. Совершенные коды.

Код Хэмминга в то же время является уникальным по структуре объектом, обладающим несколькими интересными свойствами. Это линейный код, это совершенный код, Код, дуальный к коду Хэмминга, является эквидистантным кодом.

Описать код – это описать множество C из 2 ⁿ. Код Хэмминга принято задавать через его проверочную матрицу.

Пусть m – натуральное число. Проверочная матрица кода имеет размеры m x (2^m-1).

В столбцах находятся все ненулевые последовательности длины m, представляющие собой двоичную запись числа – номера столбца. Очевидно, что любые два столбца линейно независимы, а среди троек столбцов уже есть линейно зависимые наборы.

Поэтому, согласно приведенной выше теореме 14.1, кодовое расстояние кода Хемминга d =3. Следовательно, этот код исправляет ровно одну ошибку.

Сразу из определения проверочной матрицы кода Хэмминга следует простой алгоритм декодирования. Декодирование происходит сразу после вычисления синдрома принятого слова y. Для принятого слова y есть три возможности:

1. Ошибок не было. Тогда синдром S = y H^T=0.
2. Ошибка ровно одна. Тогда синдром является двоичной записью (индикатором) номера бита, в котором произошла ошибка, так как для линейного кода сидром – сумма столбцов проверочной матрицы, в которых произошли ошибки. В нашем случае ошибка одна, а столбец – номера столбца
3. Произошло более одной ошибки. Тогда код Хэмминга не обеспечивает защиты от ошибок.

Пример.

m = 3, n = 2³ – 1 = 7, k = 4. Пусть информационными будут символы ().

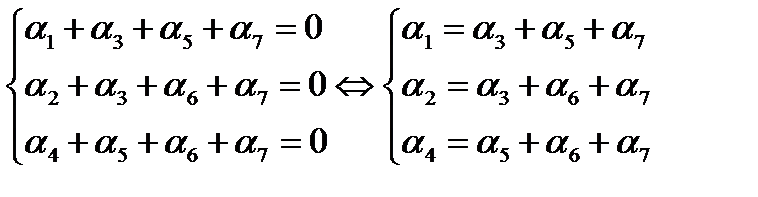
U = 1100 → 0 1 1 1 1 0 0

Если U – передано, U ’ – получено, рассмотрим 3 случая:

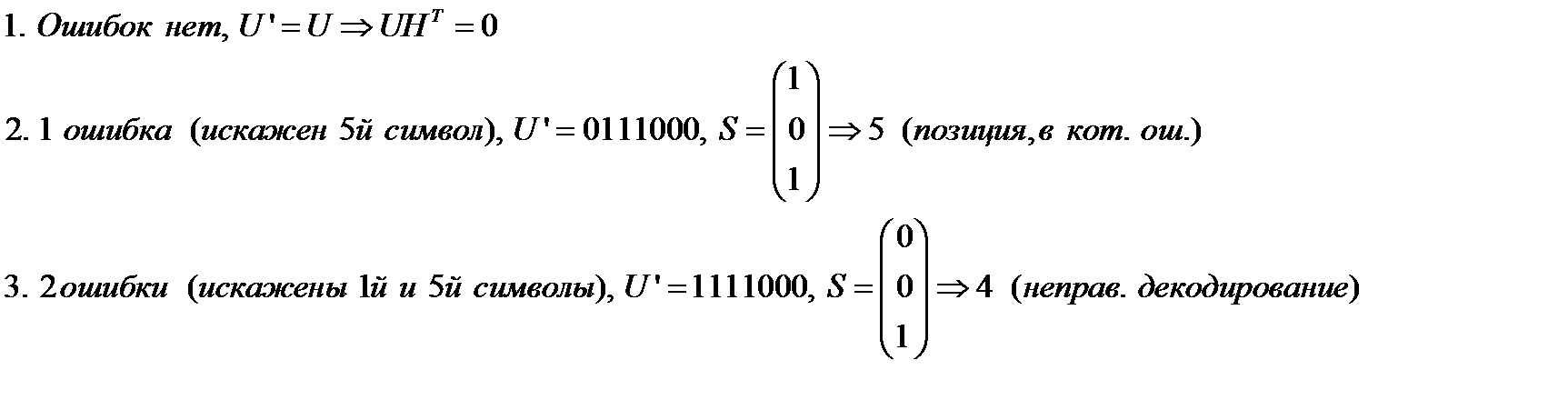 Заметим, что в данном примере .

Рассмотрим теперь свойства кода.

Длина кодовых слов n = 2 ^m – 1. Число проверочных символов m = log (n + 1). Число информационных символов равно 2 ^m – 1 -  m. Отсюда следует, что число кодовых слов | C |  в коде Хэмминга | C | = 2 ⁿ / (1 + n).

Заметим теперь, что число точек в шаре радиуса единица равно 1 + n, и вспомним приведенную выше границу Хэмминга:

.

Код Хемминга исправляет одну ошибку и   A (n, 3) = 2 / (1 + n). Получаем, что для  Хемминга граница Хемминга достигается, шары вокруг кодовых точек покрывают все пространство Bⁿ.

Определение. Код С, исправляющий t ошибок, называется совершенным, если .

То есть, совершенный код – код, на котором достигается граница Хемминга.

Таким образом, мы доказали утверждение.

Теорема 15.1. Код Хэмминга является совершенным кодом.

Применим теперь теорему Маквильямс.

Так как код Хэмминга - совершенный код, то число кодовых точек веса s, попавших хотя бы в один шар радиуса единица с центром в кодовой точке, равно общему числу точек веса s, т.е. C (s) = C^S_n.

Применяя Следствие 3из теоремы Маквильямс, получаем

.

Но φ₁(n-1,-1)=2^n-k. Тогда

, т.е.

.

Т.к. многочлен равен нулю, то все его коэффициенты равны нулю:

Но  Отсюда следует, что  только при i=(n+1)/2, т.е.

 

  b ₁ = b ₂ = … = b _{(n – 1) / 2} = b _{(n + 3) / 2} = … = b_n = 0.

 Тогда: n – 2 i + 1 = 0, а i = (n + 1) / 2.

Т.е. b _{( n – 1) / 2} не равно 0, а значит спектр кода V * равен (0, 0…0, (n + 1) / 2, 0…0).

Заметим, кроме того, что справедливо равенство:

(n+1)/2=2^m-1.

Получаем интересный код, который принадлежит к определенному классу.

То есть код, двойственный к коду Хэмминга обладает тем свойство, что попарные расстояния между его кодовыми точками одинаковы и равны (n+1)/2.

Эквидистантные коды.

Определение. Код называется эквидститантным, если для любых i, j (i ≠ j):   ρ (v_j, v_i) = d.

Таким образом, мы доказали следующее утверждение.

Теорема 15.2. Код, двойственный коду Хемминга является эквидистантным кодом.

Этот код называется кодом Макдональда.

Параметры кода Макдональда: n = 2 ^m – 1, k = m, d=(n+1)/2.

Тогда все ρ (…) = 2 ^{m – 1} (число точек в коде Макдональда 2 ^m)

Применим теорему Плоткина: A (n, d) ≤ 2 d / (2 d – n) для кода Макдональда и получим:

2 d / (2 d – n) = 2*2 ^{m -1} / 2*2 ^{m -1} – (2 ^m – 1) = 2 ^m

Отсюда следует, что  любой эквидистантный код не может содержать более чем 2 ^m точек. Поэтому код Макдональда оптимален, лучше ничего не построить.

Оказывается «мощностное свойство» кода Макдональда справедливо для любых эквидистантных кодов.

Теорема 15.3.  Пусть V – эквидистантный линейный код в Bⁿ, тогда | V | ≤ n + 1.

Доказательство. Пусть V = (V ¹,…,V ^s), и при этом ρ (V _j, V _i) = d, если   i ≠ j.

Тогда имеем

Будем считать, что 0 V и пусть это будет первый вектор кода, т.е.

.

Определитель Грама для векторов :

 - линейно независимы.

Итак, имеем S- 1 линейно независимых векторов.

В пространстве Bⁿ  может быть не более n линейно независимых векторов

  S   n +1.

Теорема доказана.

Грубо говоря, требование симметрии типа эквидистантности приводит к тому, что в коде остается всего порядка log(| Bⁿ  |) точек.

БЧХ – коды.

Основные идеи.

В начале 1950-х годов в теории кодирования была поставлена задача построить возможное обобщение кода Хэмминга - код, исправляющий t ошибок. Для этого потребовалось порядка 10 лет.

С этими кодами вы уже знакомы по курсу алгебры. Так что приведенная ниже иллюстрация и обсуждения даны просто в качестве «дополнения» к нашему курсу.

Стояла задача построить  (n,k)- код с минимальным числом строк проверочной матрицы и заданным кодовым расстоянием d. Обозначим это минимальное число строк такого кода через m(n,d).

В основу легли идеи:

1. Построить такую проверочную матрицу, у которой кодовое расстояние 2 t + 1 (2 t столбцов линейно-независимы).
2. Используя алгебраические свойства кода, построить алгоритм кодирования (декодирования).
3. Определитель Вандермонда

для матрицы, состоящей из различных элементов поля (α_i≠α_j; i,j=1,…,n) не равен нулю, поэтому любые d-1 столбцов этой матрицы линейно независимы.

Рассмотрим построение проверочной матрицы. Пусть l₁, l₂, …, l_t - локаторы ошибок – двоичные записи номеров битов, в которых произошли ошибки. Тогда проверочная матрица строится так, что ее строки задают проверочные отношения по следующей схеме:

 

Получаем t уравнений с t неизвестными,  при декодировании решаем их и находим, где произошли ошибки.

Предыдущая45678910111213141516171819Следующая

Поделиться:

Воспользуйтесь поиском по сайту: