Пример кода, исправляющего две ошибки.

Опишем на следующем примере основную идею декодирования.

Пример. Рассмотрим БЧХ-код, исправляющий две ошибки. 

Его проверочная матрица состоит из двух половин: первая половина (верхняя часть матрицы) – та же, что и у кода Хэмминга. Предположим, что множество вектор - столбцов верхней половины – элементы поля. (Т.е. их можно складывать, вычитать, умножать и делить.) Тогда вторая половина проверочной матрицы – значения некоторой функции  f(i)  от векторов первой половин, например, столбцы первой, возведенные в куб (нельзя брать квадраты, потому что квадрат суммы в некоторых полях равен сумме квадратов).

В этом случае первая половина γ вектора синдрома задает, как и раньше, сумму позиций i  и j, в которых произошла ошибка, а вторая половина - δ – сумму кубов этих позиций. Если произошло две ошибки, то мы получаем два уравнения с двумя неизвестными. Решаем их (а в поле это можно сделать!) и находим позиции ошибок.

Сказанное проиллюстрировано ниже.

Мы имеем систему двух уравнений с двумя неизвестными:

В поле GF(2ⁿ) (см. Замечание ниже) можно получить:

.

Отсюда

.

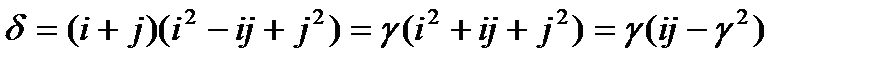Тогда удовлетворяют уравнению .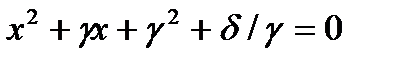

Это уравнение решается в поле GF(2ⁿ) и всегда имеет там два корня.

Замечание.

На практике вектора  i и j называются векторами локаторов ошибок (или просто локаторами ошибок), а многочлен, корнями которого являются вектора, мультипликативно обратные локаторам ошибок, называется многочленом локаторов ошибок. И именно он используется в алгоритмах кодирования и декодирования, вместо приведенного выше.

В общем случае это следующий многочлен:

,

где произведение берется по всем локаторам ошибок.

Для нашего примера о н выглядит так: .

Основная теорема.

Пусть α ₁… α _n – элементы поля GF (2 ^k), а γ ₁,γ ₂,…, γ _i - соответствующие им двоичные векторы, записанные в виде столбцов. Эьл элементы поля, которое вы знаете, как строить.

Рассмотрим матрицу.

-  (0,1)-матрица размера knxn.

Теорема 15.4. Любые 2 S столбцов матрицы  M линейно-независимы.

Доказательство. От противного. (Всюду «+» означает сложение по mod 2.

Заметим, что

(α ₁ + … + α _n)² = α ₁² + … + α _n ²          (15.1)

Пусть существует h столбцов (h ≤ 2 S), являющихся линейно-зависимыми. Это столбцы с номерами i ₁… i_h, тогда

γ ^{2 t -1} _{i 1} + … + γ ^{2 t -1} _ih = (0…0) ^T, t = 1… S

Если перейти к элементам поля получим:

α ^{2 t -1} _{i 1} + … + α ^{2 t -1} _ih = 0, t = 1… S                (15.2)

Для любого четного q (1 ≤ q ≤ 2 S): можно представить q = 2 ^U (2 t – 1), U ≥ 1, t ≤ S

Применим соотношение (15.1) к равенству (15.2) U раз и получим:

α ^q _{i 1} + … + α ^q _in = 0.  (15.3)

Таким образом

α ^j _{i 1} + … + α ^j _in = 0 при j=1,…,2S.

Возьмем матрицу M, определитель любого  минора порядка (d – 1) будет представлять собой определитель Вандермонда порядка d – 1. А он не равен нулю.

Теперь возьмем d = 2 S + 1, т.о. любой минор порядка 2 S не равен 0. Отсюда следует, что любые 2 S столбцов линейно-независимы.

Получили противоречие с  соотношением (15.3).

Теорема доказана.

Следствие. Матрица   может быть проверочной матрицей (n, k) – кода, исправляющего S ошибок.

Примеры.

Код Хэмминга является БЧХ-кодом с кодовым расстояние 3 и исправляет одну ошибку.

В приведенном выше примере проверочная матрица кода с расстоянием 5 строится из двух частей. Верхняя часть – проверочная матрица кода Хэмминга. Нижняя половина – столбцы верхней половины, возведенные в куб (эти столбцы трактуются как элементы описанного выше поля. Схема декодирования приведена выше.

Для случая трех ошибок проверочная матрица состоит уже из трех частей. Третья часть – это столбцы первой части, возведенные в пятую степень. Многочлен денумераторов ошибок имеет третью степень. Пусть произошло 3 ошибки в позициях η, δ, ζ. Тогда при рассмотрении верхней части матрицы η + δ + ζ = ρ ^*; второй части: η ³ + δ ³ + ζ ³ = ρ ^**; третьей части: η ⁵ + δ ⁵ + ζ ⁵ = ρ ^***. Получаем систему из трех уравнений с тремя неизвестными.

Теория и алгоритмы решения уравнений в конечных полях хорошо разработаны, поэтому решение уравнений в алгоритме декодирования БЧХ-кода не представляет труда. Конечно, чем больше S, тем больше сложность алгоритма.

Число проверочных символов БЧХ-кода для исправления S ошибок (упомянутое выше минимальное число строк проверочной матрицы) подчиняется соотношению:

m(n,d) ~ s log n

k = n – s log n при n → ∞, k → n.

Утверждение. Для любой бесконечной последовательности (n,k,d)-кодов БЧХ над GF (q) скорость кода k/n и отношение d/n стремятся к нулю с ростом n.

Определение. Линейный код длины п называется циклическим, если для любого кодового слова (x₁,x₂,..., x_n) слово (x₂,..., x_n,x₁) также является кодовым.

В курсе алгебры вам было доказано, что БЧХ-код является циклическим кодом.

Циклические коды обладают несложными процедурами кодирования и декодиро­вания, имеют хорошие алгебраические свойства, их группы автоморфизмов содержат циклические подстановки. Все совершенные линейные коды, коды Рида-Маллера и другие коды являются кодами, которые после пе­рестановки координат и несущественной модификации оказываются циклическими. Многие важнейшие блоковые коды, открытые позже, также оказались либо циклическими, либо тесно связанными с ними.

Построение БЧХ-кодом явилось качественным прорывом не только в такой математической дисциплине как теория кодирования, но и в инженерных технологиях защиты информации от шума в канале.

Выше мы уже упоминали о том, что в протоколах передачи информации встают вопросы синхронизации скорости генерации кодовых слов, скорости передачи и пропускной способности канала.

Таким же важным вопросам для адаптивных протоколов является подбор соответствия корректирующей способности кода и качества канала. Очевидно, что при вероятности ошибки в канале p=0,2 и длине кодового слова n=10 использование кода с d=4 или даже 5 означает сознательное согласие на то, что информация будет частично искажаться. Если же кодовое расстояние будет, например, 20, то вероятность искажения информации будет меньше, чем 10^-10.

Отсюда следует, что при построении протокола передачи необходимо учитывать такие свойства информации, как важность, ценность, чувствительность к искажению. Для их учета нужно уметь их измерять (кодировать в широком смысле!). Но для этого нужно дать им определение.

Как ни странно, на сегодня этот вопрос еще малоизучен. В протоколах передачи в лучшем случае используются эвристики и экспертные оценки. Типичный подход: «Данная информация является важной и требует передачи с гарантией безошибочности P_γ=10^-9.»

А если мы хотим передавать по каналу разные типы информации? На практике для этого используются не только разные каналы, но и разные сети. В то же время, с математической точки зрения, очевидно, что, зная p, n и P_γ, можно подобрать d.

Такого сорта протоколы нельзя построить, имея в своем распоряжении только код, исправляющий одну ошибку. Именно появление кодов с различными значениями параметра d (например, БЧХ-кодов) дало такую возможность.

Предыдущая45678910111213141516171819Следующая

Поделиться:

Воспользуйтесь поиском по сайту: