 |
Т Е С Т по теме «Перпендикулярность плоскостей».1 часть. 1 глава
|
|
|
|
1.Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то как расположена вторая прямая по отношению к третьей?
а) параллельна;б) перпендикулярна; в) скрещивается; г) совпадают;
2.Если две прямые перпендикулярны к плоскости, то как они расположены по отношению друг к другу?
а) параллельны; б) перпендикулярны; в) скрещиваются; г) пересекаются;
3.Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то как расположена эта прямая по отношению к плоскости?
а) параллельна плоскости; б) перпендикулярна к плоскости;в) лежит в плоскости;
4.Прямая а параллельна плоскости α, а прямая b перпендикулярна к этой плоскости. Как расположены прямые а и b?
а) параллельны; б) перпендикулярны; в) скрещиваются; г) совпадают;
5.Сколько прямых, перпендикулярных к данной плоскости проходит через данную точку пространства?
а) одна; б) две; в) ни одной; г) бесконечное множество;
6.Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то как расположены такие плоскости?
а) параллельны; б) перпендикулярны; в) скрещиваются; г) совпадают;
7.Сколько двугранных углов имеет параллелепипед?
а) четыре; б) восемь; в) десять; г) двенадцать;
8.Диагональ квадрата перпендикулярна к некоторой плоскости. Как расположена другая диагональ квадрата по отношению к этой плоскости?
а) параллельна плоскости; б) перпендикулярна к плоскости;
в) лежит в плоскости; г) пересекает плоскость;
9.Каждая из плоскостей α и β перпендикулярна к плоскости γ. Каково взаимное расположение плоскостей α и β?
а) параллельны; б) перпендикулярны; в) совпадают; г) скрещиваются;
10.Что больше: перпендикуляр, проведенный из данной точки к плоскости или наклонная проведенная из той же точки к этой плоскости?
|
|
|
а) перпендикуляр; б) наклонная; в) они равны;
2 часть.
1. Расстояние от некоторой точки до плоскости квадрата равно 4 см, а до каждой из его вершин – 6 см. Найдите диагональ квадрата.
А) 2  см; Б) 5 см; В) 5
см; Б) 5 см; В) 5  см; Г) другой ответ.
см; Г) другой ответ.
2. Через вершину квадрата ABCD проведена прямая AM, перпендикулярная его плоскости. Какое из данных утверждений неверно?
А) MA перпендикулярна BD; В) MB перпендикулярна CB;
Б) MD перпендикулярна СD; Г) MC перпендикулярна СB.
3. Найдите расстояние от середины отрезка АВ, пересекающего плоскость α,до плоскости α, если расстояния от точек А и В до плоскости равны соответственно 7 см и 9 см. А) 8 см; Б) 1 см;
В) 4 см; Г) другой ответ.
4. Расстояния от вершин А, В, С параллелограмма ABCD, не пересекающего плоскость α, до плоскости α равны соответственно 3 см, 15 см и 18 см. Найдите расстояние от вершины D до плоскости α.А) 3  см; Б) 3 см; В) 6 см; Г) другой ответ.
см; Б) 3 см; В) 6 см; Г) другой ответ.
5. Точка А находится на расстоянии 3 см и 5 см от двух перпендикулярных плоскостей α и β. Найдите расстояние от точки А до прямой пересечения плоскостей α и β.
А) 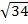 см; В) 4 см; В) 6 см; Г) другой ответ.
см; В) 4 см; В) 6 см; Г) другой ответ.
6. Из вершины равностороннего треугольника АВС проведен перпендикуляр АК к плоскости треугольника. Точка D – середина стороны ВС. Найдите длину АК, если ВС = 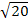 см, КD = 8 см.
см, КD = 8 см.
А) 14 см; В) 12 см; В) 7 см; Г) другой ответ.
7. Расстояние от некоторой точки до плоскости прямоугольника равно 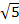 см, а до всех его вершин – 3 см. Найдите диагональ прямоугольника. А) 4 см; Б) 2 см; В) 5 см; Г) другой ответ.
см, а до всех его вершин – 3 см. Найдите диагональ прямоугольника. А) 4 см; Б) 2 см; В) 5 см; Г) другой ответ.
8. Найдите расстояние от середины отрезка АВ, пересекающего плоскость α,до плоскости α, если расстояния от точек А и В до плоскости равны соответственно 4 см и 10 см.
А) 7 см; Б) 3 см; В) 2 см; Г) другой ответ.
9. Расстояния от вершин А, В, С параллелограмма ABCD, не пересекающего плоскость α, до плоскости α равны соответственно 19 см, 6 см и 16 см. Найдите расстояние от вершины D до плоскости α. А) 23 см; Б) 11 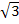 см; В) 29 см; Г) другой ответ.
см; В) 29 см; Г) другой ответ.
|
|
|
10. Точка А находится на расстоянии 2 см и 3 см от двух перпендикулярных плоскостей α и β. Найдите расстояние от точки А до прямой пересечения плоскостей α и β. А) 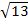 см; В)
см; В) 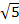 см; В) 3 см; Г) другой ответ.
см; В) 3 см; Г) другой ответ.
11. Из вершины равностороннего треугольника АВС проведен перпендикуляр АК к плоскости треугольника. Найдите длину АК, если ВС = 3 см, КС = 3  см.
см.
А) 2 см; В) 3 см; В) 4 см; Г) другой ответ.
Инструкционная карта
ПР № 3 «Построение многогранников. Вычисление площадей и объемов многогранников».
Задание:
 1) Перепишите и заполните пропуски:
1) Перепишите и заполните пропуски:
Ø А)Пример 1. Высота правильной треугольной пирамиды 4 см, а ее апофемы 8 см. Вычислите площадь боковой поверхности пирамиды.
Решение: Исходя из того, что MK = 8, MO = 4, синус угла OKM равен MO/MK = 1/2,откуда угол равен arcsin 1/2 = 30 °. Откуда KO / MK = cos 30°, KO / 8 = cos 30°,
KO = 8 cos 30°.KO = 8  /2 = 4
/2 = 4  .
.
Тогда по свойству равностороннего треугольника КО = r = a  /6.
/6.
4  = a
= a  /6, a = 24.
/6, a = 24.
Теперь, зная размер основания боковой грани и ее апофему, найдем площадь боковой грани как площадь равнобедренного треугольника: Sт = 1/2  24
24  8 = 12
8 = 12  8 = … см2.
8 = … см2.
Откуда площадь боковой поверхности пирамиды S = 3 Sт = 3  96 = … см2.
96 = … см2.
Ответ: 288 см2.
Пример 2. Дано:усеченная правильная пирамида, n = 3, h = 4, a 1= 16  , a 2= 10
, a 2= 10  . Надо найти площадь полной поверхности усеченной пирамиды.
. Надо найти площадь полной поверхности усеченной пирамиды.
Решение: r1= a 1 / 2  = 16
= 16  : 2
: 2  = 16: 2 = …, r2= a 2 / 2
= 16: 2 = …, r2= a 2 / 2  = 10
= 10  : 2
: 2  = 10: 2 = …,
= 10: 2 = …,
l 2 = h2 + (r2  r1)2, l 2 = 42 + (5
r1)2, l 2 = 42 + (5 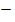 8)2 = 16 + 9 = …, l = …Sn =
8)2 = 16 + 9 = …, l = …Sn = 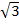 /4
/4  (a 12 + a 22) + 1,5
(a 12 + a 22) + 1,5 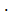 l
l  (a 1 + a 2).
(a 1 + a 2).
Sn =  /4
/4  ((16
((16  )2 + (10
)2 + (10  )2) + 1,5
)2) + 1,5 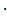 5
5 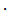 (16
(16  + 10
+ 10  ) =
) =  /4
/4  (768 + 300) + 1,5
(768 + 300) + 1,5 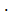 5
5 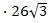 = =267
= =267 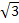 + 195
+ 195  = …
= …  .
.
Ответ: 462 
Пример 3. Дано: усеченная правильная пирамида, n = 4, h = 3, a 1= 16, a 2= 8. Надо найти площадь полной поверхности усеченной пирамиды.
Решение: r1= a 1 / 2 = 16: 2 = …, r2= a 2 / 2 = 8: 2 = …,
l 2 = h2 + (r2  r1)2, l 2 = 32 + (4
r1)2, l 2 = 32 + (4  8)2 = 9 + 16 = …, l = ….
8)2 = 9 + 16 = …, l = ….
Sn = (a 12 + a 22) + 2 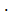 l
l 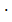 (a 1 + a 2).Sn = (162 + 82) + 2
(a 1 + a 2).Sn = (162 + 82) + 2 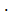 5
5 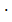 (16 + 8) = 320 + 240 = ….
(16 + 8) = 320 + 240 = ….
Ответ: 560
Пример 4. Дано: усеченная правильная пирамида, n = 6, h = 2, a 1= 2, a 2= 6. Надо найти площадь полной поверхности усеченной пирамиды.
Решение: r1= a 1 / 2 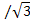 = 2: 2
= 2: 2 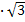 =
=  , r2= a 2 / 2
, r2= a 2 / 2 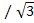 = 6: 2
= 6: 2 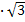 = 3
= 3  ,
,
l 2 = h2 + (r2  r1)2, l 2 = 22 + (
r1)2, l 2 = 22 + (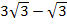 )2 = 4 + 12 = …, l = ….
)2 = 4 + 12 = …, l = ….
Sn =3 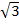 /2
/2  (a 12 + a 22) + 3
(a 12 + a 22) + 3 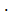 l
l 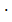 (a 1 + a 2).Sn =3
(a 1 + a 2).Sn =3 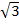 /2
/2  (22 + 62) + 3
(22 + 62) + 3 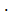 4
4 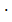 (2 + 6) = …
(2 + 6) = …  + ….
+ ….
Ответ: 60  + 96
+ 96
Пример 5. Дано: усеченная правильная пирамида, n = 4, h = 3, r1=2, r2= 6. Надо найти площадь полной поверхности усеченной пирамиды.
|
|
|
Решение: l 2 = h2 + (r2  r1)2, l 2 = 32 + (6
r1)2, l 2 = 32 + (6  2)2 = 9 + 16 = …, l = ….
2)2 = 9 + 16 = …, l = ….
Sn = 4 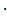 (r12 + r22) + 4
(r12 + r22) + 4 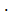 l
l 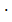 (r1 + r2).Sn = 4
(r1 + r2).Sn = 4 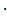 (22 + 62) + 2
(22 + 62) + 2 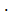 5
5 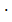 (2 + 6) = 160 + 80 = ….
(2 + 6) = 160 + 80 = ….
Ответ: 240.
Ø В)Пример 1. Площадь грани прямоугольного параллелепипеда равна 12. Ребро,
перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Решение: Каждая грань прямоугольного параллелепипеда –прямоугольник.
Пусть SABCD= a 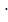 b = 12, тогда АА1= h = 4, т.к. АА1⊥ АВСD
b = 12, тогда АА1= h = 4, т.к. АА1⊥ АВСD
Используем формулу объема прямоугольного параллелепипеда: V = a 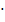 b
b 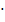 h, V = 12
h, V = 12 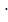 4 =...
4 =...
Ответ: 48 см3.
Пример 2. Объем прямоугольного параллелепипеда равен 12. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Решение: Пусть АА1⊥ АВСD, V = 12, АА1= h = 3.
Найдём SABCD. Используем формулу объема прямоугольного параллелепипеда V = a 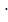 b
b 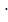 h, где SABCD= a
h, где SABCD= a 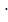 b, SABCD
b, SABCD 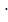 3 = 12,SABCD= 12: 3 =... Ответ: 4 см2.
3 = 12,SABCD= 12: 3 =... Ответ: 4 см2.
Пример 3. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Решение: a = 4, b = 2, d = 6. Найдем V.
Формула диагоналипрямоугольного параллелепипеда:
d2 = a2 + b2 + h2, 16 + 4 + h2 = 36, h2 = …, h =...
Формула объема прямоугольного параллелепипеда: V = a  b
b  h, V = 4
h, V = 4  2
2  4 =... Ответ: 32 см3.
4 =... Ответ: 32 см3.
Пример 4. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ и высоту.
Решение: a = 3, b = 2. Формула объема прямоугольного параллелепипеда: V = a  b
b  h, 3 . 2 .h = 36,
h, 3 . 2 .h = 36,
6h = 36, h =..., V = 36. Найдем d. d2 = 9 + 4 + 36, d2 = 49, d =...  Ответ: 7 и 6 см.
Ответ: 7 и 6 см.
Пример 5. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед, диагональ
D1B = 18 составляет угол в 30° с плоскостью боковой грани, и угол в 45° с боковым ребром (рис.). Найти: V.
Решение: BC1 - проекция D1B на плоскость боковой грани BB1С1С,
поэтому ∠D1BC1 = 30°, ∠D1BB1= 45°.
Рассмотрим ΔD1C1B: ∠D1C1B = 90° (рис.). ∠В = 30°. =>D1C1 = 18: 2 = … см.
Рассмотрим ΔD1B1B - прямоугольный: BB1= 18 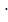 cos 45° = 18
cos 45° = 18 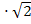 : 2 = …
: 2 = … 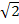 см.
см.
Диагональ (d) и измерения (а, b, с) прямоугольного параллелепипеда связаны соотношением:
d2 = a2 + b2 + h2, 182 = 92 + (9 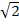 )2 + B1C12,(ΔD1B1B: B1B =D1B1).
)2 + B1C12,(ΔD1B1B: B1B =D1B1).
B1C12 = 182– 92– (9 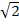 )2 = 324 – 81– 81
)2 = 324 – 81– 81 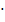 2 = 81, B1C1 = …см. V = 9
2 = 81, B1C1 = …см. V = 9  9
9  9 = …
9 = … 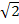 см3.
см3.
Ответ: V = 729 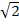 см3.
см3.
|
|
|
Пример 6. Стороны основания прямоугольного параллелепипеда 3 и 4. Найти его объём, если высота равна длине диагонали его основания.
Решение: BD - диагональ основания прямоугольного параллелепипеда. BD2 = АВ2 + АD2,
BD2 = 32 + 42 = 9 + 16 = …, BD = …,h = 5. V = 3  4
4  5 = … см3.
5 = … см3.
Ответ: 60см3.
Пример 7. Найти объём прямоугольного параллелепипеда, если стороны основания 2 и 3, а диагональ параллелепипеда 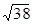 .
.
Решение: d2 = a2 + b2 + h2, (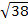 )2 = 22 + 32 + h2, h2 = 38 – 4
)2 = 22 + 32 + h2, h2 = 38 – 4  9 = 25, h =...V = 2
9 = 25, h =...V = 2  3
3 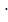 5 = … см3.
5 = … см3.
Ответ: 30 см3.
Ø 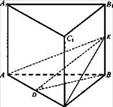
|
 h, S = BC2: 2, BC2 = BN2 + CN2, BN =CN
h, S = BC2: 2, BC2 = BN2 + CN2, BN =CN(ΔABC – прямоугольный,AC =BC), ΔC1CN – прямоугольный, ∠CNC1 = 45°,
CC1 = CN= 6, BC2 =2CN2 = 2
 62 = 2
62 = 2  36 = …, BC = 6
36 = …, BC = 6 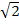 ,
, V = (6
 2
2 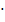 6: 2 = 36
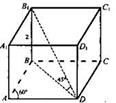
6: 2 = 36 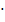 6 = … см3. Ответ: 216см3. Пример 2. Дано: ABCDА1В1С1D1 - прямая призма, ABCD - ромб, ∠BAD = 60° (рис.). ВВ1 = 2, ∠B1DB = 45°. Найти: V. Решение: Sp = AB
6 = … см3. Ответ: 216см3. Пример 2. Дано: ABCDА1В1С1D1 - прямая призма, ABCD - ромб, ∠BAD = 60° (рис.). ВВ1 = 2, ∠B1DB = 45°. Найти: V. Решение: Sp = AB 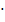 AD
AD 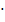 sin 60°. ΔABD – равносторонний(AB = AD, ∠BAD = 60° ).
sin 60°. ΔABD – равносторонний(AB = AD, ∠BAD = 60° ).AB = BD = AD. ΔB1DB –прямоугольный,
∠B1DB = 45°. =>ΔB1DB – равнобедренный, ВВ1 = ВD = 2,
V = AB
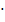 AD
AD 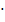 sin 60°
sin 60° 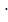 BB1= BB13
BB1= BB13 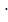 sin 60° = 23
sin 60° = 23  / 2 = …
/ 2 = …  см3.
см3.
Ответ: 4  см3.
см3.
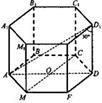 Пример 3. Дано: ABCDFM...M1 - правильная шестиугольная призма. AD1 = 8 см - наибольшая диагональ.∠AD1D = 30°(рис.).
Пример 3. Дано: ABCDFM...M1 - правильная шестиугольная призма. AD1 = 8 см - наибольшая диагональ.∠AD1D = 30°(рис.).
Найти: V.
Решение: V= S0 · h. h = DD1 в ΔADD1, ∠D = 90°. ∠D1 = 30°,
DD1 = AD1 · cos 30°. DD1 = 8 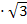 / 2 = …
/ 2 = …  , AD = AD1: 2 = 8: 2 = … см,
, AD = AD1: 2 = 8: 2 = … см,
OD = OC = CD = AD: 2 = 4: 2 = … см,
S0 = 6S ΔOCD= 6  / 4)
/ 4) 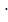 a 2 = 6
a 2 = 6  / 4)
/ 4) 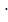 22 = 6
22 = 6  см. V = 6
см. V = 6 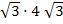 = 6
= 6 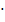 4
4  3 = … см3.
3 = … см3.
 Ответ: 72 см3.
Ответ: 72 см3.
Пример 4. Дана трапеция, S(BB1C1C) = 8 см2, S(AA1D1D) = 12см2, BH = 5 см (рис.).Найти: Vnp.
Решение: 1)Расстояние между параллельными плоскостями ВВ1С1 и AA1D1 есть длина перпендикуляра ВН, который является высотой трапеции ABCD.
|
|
|


