 |
Способ. «Кусочно-линейная функция».
|
|
|
|
Графиком кусочно-линейной функции является ломаная линия. Для построения графика находят уравнения звеньев ломаной.
Пример 1. Построить график функции 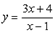
Решение:
Дана функция  . Преобразуем
. Преобразуем 
1. Область определения: 
2. Область значений: 
3. Четность, нечетность: и ни четная, ни нечетная 
4. Монотонность: убывает во всей области определения  .
.
5. Пересечение с осями 0 x и 0 y: 
6. Промежутки знакопостоянства:

 ,
,  .
.
7. Поведение функции вблизи точек разрыва и при  :
:

По результатам решения строим график.
Комментарий. При построении графика функции следует найти точки, в которых он пересекает оси координат, а также выяснить поведение функции при x, стремящемся к  в случае, когда ее
в случае, когда ее  область определения не ограничена. Необходимо также исследовать поведение функции вблизи тех точек, в которых она не определена.
область определения не ограничена. Необходимо также исследовать поведение функции вблизи тех точек, в которых она не определена.
Пример 2. Построить графики следующих функций:  .
.
Решение:
1.  Рассмотрим функцию
Рассмотрим функцию  . Она определена на всей оси 0 x, четная. Ее график состоит из двух лучей, выходящих из начала координат и направленных по биссектрисам I и II координатных углов.
. Она определена на всей оси 0 x, четная. Ее график состоит из двух лучей, выходящих из начала координат и направленных по биссектрисам I и II координатных углов.
2. Обратимся к функции  . Она определена на всей оси 0 x, четная. На рисунке приведен ее график, причем он построен из двух половинок y = 2x, при x ≥ 0 и y = 2-x, при x < 0:
. Она определена на всей оси 0 x, четная. На рисунке приведен ее график, причем он построен из двух половинок y = 2x, при x ≥ 0 и y = 2-x, при x < 0:
3.  Функция определена на всей оси 0 x, они четная:
Функция определена на всей оси 0 x, они четная:
Поскольку знаменатель дроби 1 + x2 ≥ 1 при любом x, то 0 < y ≤ 1. В точке x = 0 функция достигает своего 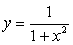 наибольшего значения. При неограниченном возрастании x величина y становится сколь угодно близкой к нулю (стремится к нулю).
наибольшего значения. При неограниченном возрастании x величина y становится сколь угодно близкой к нулю (стремится к нулю).
Пример 3. Построить график функции 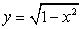 на основании результатов исследования функции.
на основании результатов исследования функции.
Решение:
Для построения графика функции исследуем ее, придерживаясь общей схемы исследования.
|
|
|
1. Нахождение области определения:
 .
.
2. Определение четности или нечетности:
 . Функция
. Функция 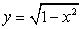 — четная.
— четная.
Дальнейшее исследование будем проводить для  .
.
3. Область изменения функции.
Если x = 1, то y = 0. Если 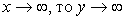 . Следовательно,
. Следовательно,  .
.

4. Пересечение с координатными осями.
Если. Пересечений с осью 0 y нет, т.к. x = 0 не входит в область определения функции.
5. Выделение промежутков монотонности.
Для x1 > x2 ≥ 1 рассмотрим разность:
 .
.
 При возрастании значений x от 1 до ∞ значения y возрастают.
При возрастании значений x от 1 до ∞ значения y возрастают.
6. Нахождение корней функции и промежутков знакопостоянства.
Если  при x = 1,
при x = 1,  при всех
при всех  .
.
По результатам исследований строим график функции 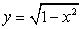
Пример 4. Примеры функций.


2) Решить задание:
1. С помощью графиков определите, сколько решений имеет система уравнений: 
2. Постройте график функции у = х2 + х – 6.
Используя график, решите неравенство х2 + х – 6 < 0.
3. Постройте график функции у= 2х2 найдите:
 а) значение функции, если х=10; х=–12;
а) значение функции, если х=10; х=–12;
б) значение аргумента, если у=4; у=–5.
4. Постройте график у =  найдите:
найдите:
а) значение y, если х=10; х=–8; б) значение x, если у=11;у=–7. 
5. По графику функции у=0,5х+3 найдите:
а) значение функции, если х=10; х=–12;
б) значение аргумента, если у=4; у=–5.
6. Постройте график функции у=–2х
- Решите графически систему уравнений:

8. Постройте график функции у= 0,5х2 найдите:а) значение функции, если х=10; х=–12;
б) значение аргумента, если у=4; у=–5.
9. Постройте график функции:
 .
.
10. Постройте график функции и запишите ее свойства (область определения, область значений, нули функции, промежутки знакопостоянства, промежутки монотонности):
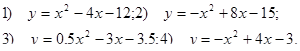
Инструкционная карта
ПР № 20 «Построение графиков периодических функций».
Задание:
1) Перепишите и заполните пропуски:
Пример 1. Определить возрастает или убывает функция: а)y = cosx при  ,
,
б)y = sinx при  ,в) у =tgx при
,в) у =tgx при  .
.
Решение: а)убывает,…,б) …, возрастает, в) возрастает.
|
|
|
Ответ: а)…, возрастает,б) убывает, …, в)...
Пример 2. Нацдите х, при котором функция пересекает ось ох: а) y = cosx при  ,
,
б) y = sinx при  ,в) у =tgx при
,в) у =tgx при  .
.
Решение: а)  ,б)
,б)  ,в)
,в)  .
.
Ответ: а)  ,б)
,б)  ,в)
,в)  .
.
Пример 3. Определить принимает положительные или отрицательные значения функция:
а) y = cosx при 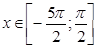 ,б) б)y = sinx при
,б) б)y = sinx при  ,в) у =tgx при
,в) у =tgx при  .
.
Решение: а)положительные при  ,отрицательные при
,отрицательные при  ,
,
б) положительные при  ,отрицательные при
,отрицательные при  ,
,
в) положительные при 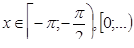 ,отрицательные при
,отрицательные при  .
.
Ответ: а)положительные при  ,отрицательные при
,отрицательные при 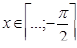 ,
,
б) положительные при  ,отрицательные при
,отрицательные при  ,
,
в) положительные при  ,отрицательные при
,отрицательные при  .
.
Пример 4. Построить график функции по таблице:
а) y = 2cosx, б) y = 6sinx.
| х | 
| 0 | 
| 
| 
|
| у | 0 | 2 | 0 |  2 2
| 0 |
| х | 
| 0 | 
| 
| 
|
| у |  6 6
| 0 | 6 |  6 6
| 0 |
Решение:
а) б)


Пример 5. Сравнить а)  и
и  , б)
, б)  и
и  .
.
Решение: а)  <
<  , (0<
, (0<  <
<  <
<  ),б)
),б)  >
>  . Ответ:: а)
. Ответ:: а)  <
<  ,б)
,б)  >
>  .
.
2) Решить задание (по примерам):
1. Определить возрастает или убывает функция: а)y = cosx при  ,
,
б)y = sinx при  ,в) у =tgx при
,в) у =tgx при  .
.
2. Нацдите х, при котором функция пересекает ось ох: а) y = cosx при  ,
,
б) y = sinx при  ,в) у =tgx при
,в) у =tgx при 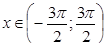 .
.
3. Определить принимает положительные или отрицательные значения функция:
а) y = cosx при  ,б) б)y = sinx при
,б) б)y = sinx при  ,в) у =tgx при
,в) у =tgx при 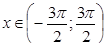 .
.
4. Построить график функции по таблице:
а) y = 6cos x.
| x | 
| 0 | 
| 
| 
|
| y | 0 | 6 | 0 | –6 | 0 |
б) y = 4sinx.
| x | 0 | 
| 
| 
| 
|
| y | 0 | 4 | 0 | –4 | 0 |
5. Сравнить а)  и
и  , б)
, б)  и
и  .
.
3) Решить задание:
1. Построить график функции y = ctgx; запишите свойства этой функции, используя свойства функции y = tgx, и то что эти функции взаимо обратны.
2. Сравнить числа: а) 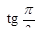 и
и  , б) tg 2,3 и tg 3, в)
, б) tg 2,3 и tg 3, в)  и
и  , г) tg 1 и tg 1,5.
, г) tg 1 и tg 1,5.
3. Построить график функции по таблице: y = sin 4x.
| x | 0 | 
| 
| 
| 
|
| y | 0 | 1 | 0 | –1 | 0 |
4. Построить график функции по таблице: y = cos 4x.
| x | 0 | 
| 
| 
| 
|
| y | 1 | 0 | – 1 | 0 | 1 |
5. Построить график функции по таблице: y = tg2x.
| x | 0 | 
| 
| 
| 
|
| y | 0 | 1 | 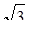
| – 1 | 0 |
6. Построить график функции по таблице: y = сtg2x.
| x | 
| 
| 
| 
| 
| 
|
| y | 0 | 1 | 0 | – 1 | 1 | 0 |
7. Построить график функции:
а) y = sin 2x, б) y = 2sinx, в) y = cos 2x, г) y = 5sinx, д) y = 4cosx,е) y = 2сtgx.
8. Построить график функции:
а) y = sin 4x, б) y = cos 4x, в) y = tg 2x, г) y = 2sinx, д) y = 2cosx, е) y = 2tgx.
Инструкционная карта
|
|
|
ПР № 21 «Построение графиков обратных функций».
Задание:
1)А) Опорный конспект.
|
|
|


