 |
Геометрическая прогрессия.
|
|
|
|
Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.
Таким образом, геометрическая прогрессия – это числовая последовательность { bn }, заданная рекуррентно соотношениями b 1 = b, bn = bn –1 q (n = 2, 3, 4…).(b и q – заданные числа, b ≠ 0, q ≠ 0).
Пример 1. 2, 6, 18, 54, … – возрастающая геометрическая прогрессия b = 2, q = 3.
Пример 2. 2, –2, 2, –2, … – геометрическая прогрессия b = 2, q = –1.
Пример 3. 8, 8, 8, 8, … – геометрическая прогрессия b = 8, q = 1.
Геометрическая прогрессия является возрастающей последовательностью, если b 1 > 0, q > 1, и убывающей, если b 1 > 0, 0 < q < 1.
Одно из очевидных свойств геометрической прогрессии состоит в том, что если последовательность является геометрической прогрессией, то и последовательность квадратов, т.е.
b 12, b 22, b 32, …, bn 2,… является геометрической прогрессией, первый член которой равен b 12, а знаменатель – q 2.
Формула n- го члена геометрической прогрессии имеет вид bn = b 1 qn– 1.
Формула суммы первых n членов прогрессии
 , или
, или  ,
,  (в случае
(в случае 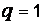 ,
,  ).
).
Если геометрическая прогрессия бесконечно убывающая ( 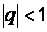 ), то ее сумма вычисляется по формуле
), то ее сумма вычисляется по формуле  .
.
Обращение периодической десятичной дроби в обыкновенную. Предположим, мы хотим обратить периодическую десятичную дробь 0,(3) в обыкновенную. Рассмотрим эту десятичную дробь в следующем виде:

Это бесконечно убывающая геометрическая прогрессия, первый член которой равен 3/10, а разность q = 1/10. В соответствии с выше приведенной формулой эта сумма равна:

Таким образом, 0,(3) = 1/3.
|
|
|
1) 
Бесконечно убывающая геометрическая прогрессия, т.к Sп= 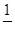 <1.
<1.
 .
.  .
.  . х-1=3. х=4.
. х-1=3. х=4.
2) 1+2х+4х 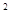 +…+(2х)
+…+(2х) 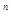 +…=3,4-1,2х
+…=3,4-1,2х  <0,5
<0,5
Бесконечно убывающая геометрическая прогрессия, т.к  <0,5.
<0,5.  .
.
Бесконечно убывающая геометрическая прогрессия (|q|<1).  .
.
Пример 1. Найдите сумму всех целых чисел, начиная от 30 и до 80 включительно.
Решение:
Сумма всех целых чисел от 30 и до 80 включительно представляет собой сумму членов арифметической прогрессии, где а1 = 30, разность d = 1, а количество членов n = 51.
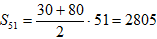 . Ответ: 2805.
. Ответ: 2805.
Пример 2. Решите уравнение 22∙24∙26∙...∙22n=(0,125)-10.
Решение:
22∙24∙26∙...∙22n=22+4+6+...+2n. 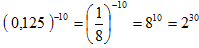 .
.
Получили: 22+4+6+...+2n=230  2+4+6+...+2n=30.
2+4+6+...+2n=30.
В левой части равенства сумма n членов арифметической прогрессии, где а1 =2, а d = 2. Согласно формуле суммы членов арифметической прогрессии имеем:
 .
.
n1 = – 6 не удовлетворяет условию т.к. n отрицательным быть не может.
n2 =5 удовлетворяет условию. Ответ: n = 5.
Пример 3. В геометрической прогрессии пятый член равен 2, восьмой равен 16. Найти сумму первых десяти членов.
Решение: Пусть (bn) – геометрическая прогрессия. Известно, что b5 = 2. По формуле n – го члена геометрической прогрессии b5 = b1 q4 = 2. Аналогично b8 = b1 q7 = 16. Поделив второе равенство на первое, получим q3 = 8, т.е. q = 2. Подставив q = 2 в первое равенство, найдём b1:
 .Согласно формуле
.Согласно формуле 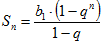 получим:
получим:  .
.
Ответ:  .
.
Пример 4. Записать число 0,6222… обыкновенной дробью.
Решение:
Запишем число 0,6222…в виде суммы: 0,6222…= 0,6 + 0,02 + 0,002 + 0,0002 + …,
где 0,02 + 0,002 + 0,0002 + … - сумма членов бесконечно убывающей геометрической прогрессии, которая находится по формуле  , где b1 = 0,02; q = 0,1.
, где b1 = 0,02; q = 0,1.
 .
.
Ответ: 28/45.
2) Решить задание:
1) Найти произведение третьего и четвёртого членов арифметической прогрессии,
если первый член равен 3, а второй равен – 2.
2) Между числами – 8,8 и 2 вставьте пять чисел так, чтобы получилась арифметическая прогрессия.
2) Третий член арифметической прогрессии в три раза меньше шестого, а сумма второго и
|
|
|
пятого равна 16. Определите первый член прогрессии
4) Найдите знаменатель геометрической прогрессии, если b1=2, b5=162.
5) В геометрической прогрессии q=0,5, b6=1/32, найти b1.
6) Найдите третий член геометрической прогрессии, если её знаменатель равен -2,
а седьмой член 16.
7) В геометрической прогрессии b1+b2+b3=31, b1+b3=26. Найти b7.
8) Какое наибольшее число последовательных нечётных чисел, начиная с 1, можно сложить,
чтобы получившаяся сумма осталась меньше 400?
9) В геометрической прогрессии b2>b1 в два раза, а b6 =64. Найти b1.
10) Найдите сумму первых пяти членов последовательности, общий член которой выражается
формулой  .
.
11) Сумма членов арифметической прогрессии с третьего по одиннадцатый включительно
равна 27. Найти номер члена прогрессии равного 3.
12) Сумма бесконечной убывающей геометрической прогрессии равна 32, а сумма пяти её
первых членов равна 31. Найдите первый член прогрессии.
13) Найдите сумму всех чётных натуральных трёхзначных чисел, делящихся на 3.
14) Вычислить сумму:  .
.
15) Найдите сумму всех положительных членов арифметической прогрессии 10,3; 8,5; ….
16) В арифметической прогрессии a10=-23. Найти a3+a17.
17) В арифметической прогрессии a5+a9=-20. Найти a7.
18) Произведение девяти первых членов геометрической прогрессии равно  .
.
Какой член геометрической прогрессии можно найти на основании этой информации? Чему он равен?
19) Решите уравнение  .
.
20) Найдите сумму  .
.
21) Три различных числа a1, a2, a3 в указанном порядке образуют арифметическую прогрессию,
а числа 2a3-a1, a2+a3-a1, a1 в указанном порядке образуют геометрическую прогрессию.
Найти знаменатель геометрической прогрессии.
3) Решить задание:
I. Пусть  – арифметическая прогрессия с разностью d и Sn – сумма n первых членов. Найти:
– арифметическая прогрессия с разностью d и Sn – сумма n первых членов. Найти:
1. a13, если a5= 2; a40= 142.
2. a1+a20, если a3+a18= 50.
3. n, если a1= 3; a2= 5; Sn= 360.
4. a1 и d, если a17+a20= 35; a16 × a21= 150.
5. a1 и d, если Sn= 2 n2- 3 n.
6. Сумму всех натуральных трехзначных чисел, не делящихся на 3.
7. Первых 100 натуральных чисел, каждое из которых при делении на 5 дает в остатке 2.
II. Пусть  – геометрическая прогрессия со знаменателем q и Sn – суммой первых n членов. Найти:
– геометрическая прогрессия со знаменателем q и Sn – суммой первых n членов. Найти:
8. b6, если b5= 36, b7= 114.
9. q, если b1= 10, b2+b3= 60.
10. b13, если b11= 25, b15= 400.
11. b1 и q, если b1+b2+b3= 62, b12+b22+b32= 2604.
12. S6, если b1=– 2, b6=– 486.
13. n, если b1= 9, bn=  , Sn= 25
, Sn= 25  .
.
14. Какому условию удовлетворяют три числа a1, a2, a3, которые одновременно являются последовательными членами как геометрической, так и арифметической прогрессий?
|
|
|
15. Решить уравнение:  .
.
16. По преданию, индийский шах позволил изобретателю шахматной игры самому назначить себе награду. Изобретатель просил, чтобы ему за первую клетку шахматной доски было дано 1 зерно, за вторую – 2, за третью – 4. В общем случае, за каждую следующую клетку в 2 раза больше, чем за предыдущую. Узнать, сколькими цифрами изображается число зерен, предназначенное изобретателю; найти это число.
17.Три числа образуют геометрическую прогрессию. Если второе число увеличить на 2, то прогрессия станет арифметической, а если после этого последнее число увеличить на 9, то прогрессия станет геометрической. Найти эти числа.
18.Решить уравнение  .
.
19.Найти a1 и d, если a11= 6; a16= 8,5.
20. Может ли число 75 быть членом геометрической прогрессии  , у которой b1=4 и q=
, у которой b1=4 и q= 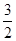 ?
?
21.Найти количество всех трехзначных натуральных чисел, делящихся на 7.
22.Доказать, что последовательность  с общим членом
с общим членом  является арифметической прогрессией.
является арифметической прогрессией.
Инструкционная карта
ПР № 29 «Составление уравнения касательной к графику функции».
Задание:
1) Перепишите и заполните пропуски:
Пример 1. Найти угловой коэффициент касательной к графику функции y = f(x) в точке с
абсциссой х₀: а) y(x) = x³, x₀ = 1, б) y(x) = lnx, x₀ = 1, в) y(x) = 3x²  4x, x₀ = 2,
4x, x₀ = 2,
г) y(x) = х3 + 7x²  5x+3, x₀ = 3, д) y(x) = е х, x₀ = ln 7, e) y(x) = 7sinx, x₀ = 0,ж) y(x) = е 3х, x₀ = ln 4.
5x+3, x₀ = 3, д) y(x) = е х, x₀ = ln 7, e) y(x) = 7sinx, x₀ = 0,ж) y(x) = е 3х, x₀ = ln 4.
Решение: угловой коэффициент k равен производной от функции в точке, т.е. k = y¢(x0),
найдем производные и вычислим их в точке x0
a)  б)
б)  в)
в) 
г) 
д)  е ln 7= …,е)
е ln 7= …,е)  7cosx,
7cosx,  7
7  cos 0 = 7
cos 0 = 7  1 = …,
1 = …,
ж)  е 3ln 4 = 3
е 3ln 4 = 3  43 = 3
43 = 3  64 = …
64 = …
Ответ: a)3, б)1, в)8,г) 64,д) 7,е)7,ж) 192.
Пример 2. а) Найти угловой коэффициент k, если 
 α = arctg 6, α = - arctg 8.
α = arctg 6, α = - arctg 8.
б) Найти α,если y(x) =  х3, x₀ = 2.
х3, x₀ = 2.
Решение: а) k =tgα = tg  k =tgα = tg
k =tgα = tg  k =tgα = tg
k =tgα = tg 
k =tgα = tg 
б) 
Ответ: а)1,  ,6,- 8, б)arctg 4.
,6,- 8, б)arctg 4.
Пример 3. Дана функция y = x 3. Составить уравнение касательной к графику этой функции в точке x 0 = 2.
Решение: Уравнение касательной: y = f ¢ (x 0) · (x − x 0) + f (x 0). Точка x 0 = 2 нам дана, а вот значения f (x 0) и f ¢(x 0) придется вычислять.
|
|
|
Для начала найдем значение функции. Тут все легко: f (x 0) = f (2) = 23 = …;
Теперь найдем производную: f ¢ (x) = (x 3) ¢ = 3 x 2;
Подставляем в производную x 0 = 2: f ¢ (x 0) = f ¢ (2) = 3 · 22 = 3  4 = …;
4 = …;
Итого получаем: y = 12 · (x − 2) + 8 = 12 x − 24 + 8 = 12 x − 16.
Это и есть уравнение касательной.
Ответ: y = 12 x − 16.
Пример 4. Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x 0 = π /2.
Решение: f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = …; f ¢(x) = (2sin x + 5)¢ = 2cos x;
f ¢(x 0) = f ¢(π /2) = 2cos (π /2) = 0;
 Уравнение касательной: y = 0 · (x − π /2) + 7 ⇒ y =...
Уравнение касательной: y = 0 · (x − π /2) + 7 ⇒ y =...
Ответ: y = 7.
Пример 5. Составьте уравнение касательной к графику функции
в точке M(3; – 2). 
Решение: Точка M(3; – 2) является точкой касания, так как 
1. a = 3 – абсцисса точки касания.2. f(3) = – 2. 3. f '(x) = x2 – 4, f '(3) = 9  4 = …
4 = …
y = – 2 + 5(x – 3), y = …x – 17 – уравнение касательной.
Ответ: y = 5x – 17.
Пример 6. Напишите уравнения всех касательных к графику функции y = – x2 – 4x + 2, проходящих через точку M(– 3; 6).
 Решение: Точка M(– 3; 6) не является точкой касания, так как f(– 3)
Решение: Точка M(– 3; 6) не является точкой касания, так как f(– 3)  6 (рис. 2).
6 (рис. 2).
1. a – абсциссаточкикасания.
2. f(a) = – a2 – 4a + 2.
3. f '(x) = – 2x – 4, f '(a) = – 2a – 4.
4. y = – a2 – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.
Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.
6 = – a2 – 4a + 2 – 2(a + 2)(– 3 – a),
a2 + 6a + 8 = 0, D = 62  4
4  1
1  8 = 36
8 = 36  32 = …,
32 = …,
а1= ( 6
6  2): 2 =
2): 2 =  8: 2 = …, а2 = (
8: 2 = …, а2 = (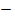 6
6 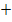 2): 2 =
2): 2 = 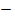 4: 2 = …,
4: 2 = …,
Если a = – 4, то уравнение касательной имеет вид y = 4x + 18.
Если a = – 2, то уравнение касательной имеет вид y = 6.
Ответ: y = 4x + 18 или y = 6.
Пример 7. Напишите уравнения всех касательных к графику функции y = x3 – 3x2 + 3, параллельных прямой y = 9x + 1.
Решение: 1. a – абсцисса точки касания. 2. f(a) = a3 – 3a2 + 3.3. f '(x) = 3x2 – 6x, f '(a) = 3a2 – 6a.
 Но, с другой стороны, f '(a) = 9 (условие параллельности). Значит, надо решить уравнение 3a2 – 6a = 9. 3a2 – 6a
Но, с другой стороны, f '(a) = 9 (условие параллельности). Значит, надо решить уравнение 3a2 – 6a = 9. 3a2 – 6a  9 = 0,
9 = 0,
D = (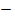 6)2
6)2  4
4  3
3  (
( ) = 36
) = 36 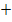 108 = …, а1= (6
108 = …, а1= (6 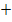 12): 6 = 18: 6 = …,
12): 6 = 18: 6 = …,
а2 = (6  12): 6 =
12): 6 = 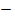 6: 6 = …,
6: 6 = …,
Его корни a = – 1, a = 3 (рис. 3).
4. 1сл.) a = – 1; f(– 1) = – 1– 3 + 3 = …; f '(– 1) = 3 + 6 = …;
y = – 1 + 9(x + 1); y = 9x + 8 – уравнение касательной;
2сл.) a = 3; f(3) = 27–27 + 3 = …; f '(3) = 27 – 18 = …;
y = 3 + 9(x – 3); y = 9x – 24 – уравнение касательной.
Ответ: y = 9x + 8 и y = 9x – 24.
 Пример 8. Напишите уравнение касательной к графику функции y = 0,5x2 – 3x + 1, проходящей под углом 45° к прямой y = 0 (рис. 4).
Пример 8. Напишите уравнение касательной к графику функции y = 0,5x2 – 3x + 1, проходящей под углом 45° к прямой y = 0 (рис. 4).
Решение: Из условия f '(a) = tg 45°,  найдем a: a – 3 = 1,a = 3 + 1 =...
найдем a: a – 3 = 1,a = 3 + 1 =...
1. a = 4 – абсцисса точки касания.
2. f(4) = 8 – 12 + 1 =...
3. f '(4) = 4 – 3 =...
4. y = – 3 + 1(x – 4). y = x – 7 – уравнение касательной.
Ответ: y = x – 7.
Пример 9. На параболе у = х2 взяты две точки с абсциссами 1 и 3. Через эти точки проведена прямая. В какой точке параболы касательная будет параллельна проведенной прямой?
|
|
|
Решение: у = х2, (1;1), (3;9). Найдем уравнение прямой  .
.
4х – 4 = у – 1. у = 4х – 3.
Прямые параллельны, если их угловые коэффициенты равны.
 - угловой коэффициент касательной в точке с абсциссой х0.
- угловой коэффициент касательной в точке с абсциссой х0.
 2х0 = 4. х0 =...,
2х0 = 4. х0 =..., 
Ответ: в точке (2;4) касательная параллельна заданной прямой.
Пример 10. При каких b и c прямые y = x и y = – 2x являются касательными к графику
функции y = x2 + bx + c?
Решение: Пусть t – абсцисса точки касания прямой y = x с параболой y = x2 + bx + c;
p – абсцисса точки касания прямой y = – 2x с параболой y = x2 + bx + c.
Тогда уравнение касательной y = x примет вид y = (2t + b)x + c – t2, а уравнение
касательной y = – 2x примет вид y = (2p + b)x + c – p2.Составим и решим систему уравнений:
 ;
;
2t = 1,5; t = 0,75;
p = – t = …,
c =  =
=  = …,
= …,
b = 1 – 2t = 1 – 2  0,75 = 1– 1,5 = …
0,75 = 1– 1,5 = …
Ответ: b = – 0,5; c = 0,562 5.
2) Решить задание (по примерам):
1. Найти угловой коэффициент касательной к графику функции y = f(x) в точке с
абсциссой х₀: а) y(x) = x4, x₀ = 1, б) y(x) = lnx, x₀ = 2, в) y(x) = 3x² - 4x, x₀ = 4,
г) y(x) = х3 + 7x² - 5x+3, x₀ =5, д) y(x) = е х, x₀ = ln 8, e) y(x) = 9sinx, x₀ = 0,ж) y(x) = е 3х, x₀ = ln 6.
2. а) Найти угловой коэффициент k, если 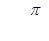
 α = arctg 9, α = - arctg 11.
α = arctg 9, α = - arctg 11.
б) Найти α,если y(x) =  х3, x₀ = 4.
х3, x₀ = 4.
3. Дана функция y = x 3. Составить уравнение касательной к графику этой функции в точке x 0 = 1.
4. Составить уравнение касательной к графику функции f (x) = 4sin x + 5 в точке x 0 = π /2.
5. Составьте уравнение касательной к графику функции  в точке M(3; – 1).
в точке M(3; – 1).
6. Напишите уравнения всех касательных к графику функции y = – x2 – 4x + 2, проходящих через точку M(– 3; 9).
7. Напишите уравнения всех касательных к графику функции y = x3 – 3x2 + 3, параллельных
прямой y = 24x + 1.
8. Напишите уравнение касательной к графику функции y = 0,5x2 – 5x + 1, проходящей
под углом 45° к прямой y = 0.
9. На параболе у=х2 взяты две точки с абсциссами 1 и 2. Через эти точки проведена прямая.
В какой точке параболы касательная будет параллельна проведенной прямой?
10. При каких b и c прямые y = x и y = – 2x являются касательными к графику
функции y = x2 + 2bx + c?
3) Решить задание:
1. Напишите уравнения касательных, проведенных к графику функции y = 2x2 – 4x + 3 в точках пересечения графика с прямой y = x + 3.
2. При каких значениях a касательная, проведенная к графику функции y = x2 – ax в точке графика с абсциссой x0 = 1, проходит через точку M(2; 3)?
3. Найдите все общие точки графика функции y = 3x – x3 и касательной, проведенной к этому графику через точку P(0; 16).
4. На кривой y = x2 – x + 1 найдите точку, в которой касательная к графику параллельна
прямой y – 3x + 1 = 0.
5. Найдите угол q между касательными к графику функции y = x3 – 4x2 + 3x + 1, проведенными в точках с абсциссами 0 и 1.
6. Прямая y = 2x + 7 и парабола y = x2 – 1 пересекаются в точках M и N. Найдите точку K пересечения прямых, касающихся параболы в точках M и N.
7. При каких значениях b касательная, проведенная к графику функции y = bx3 – 2x2 – 4 в точке с абсциссой x0 = 2, проходит через точку M(1; 8)?
8. Найти угол между касательными к графику функции 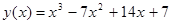 , проведенными в точках с абсциссами 1 и 2.
, проведенными в точках с абсциссами 1 и 2.
9. Является ли прямая у = х – 1 касательной к кривой у = х3 – 2х + 1?
10. Найдите уравнение касательной к графику функции 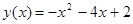 в точке с абсциссой
в точке с абсциссой  .
.
11. К графику функции у = 3(х + 2) проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой х0 = – 1. Найдите абсциссу точки, в которой
другая касательная касается графика данной функции.
12. Напишите уравнение касательной к графику функции f(x) = x2 – 4x + 5, если эта касательная проходит через точку (0; 4) и абсцисса точки касания положительна.
13. Напишите уравнение касательной к графику функции f(x) = x2 + 3x + 5, если эта касательная проходит через точку (0; 1) и абсцисса точки касания отрицательна.
14. Найдите уравнение параболы f(x) = ax2 + bx + 1 касающейся прямой у = 7х + 2
в точке М (1; 5).
15. К графику функции  провести касательную так, чтобы она была параллельна прямой у = 4х – 5.
провести касательную так, чтобы она была параллельна прямой у = 4х – 5.
16. Из точки (0; 1) провести касательную к графику функции 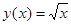 .
.
17. Составить уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой  .
.
18. Составить уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой 
19. Составить уравнение касательной к графику функции 
в точке с абсциссой 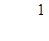 .
.
20. Составить уравнение касательной к графику функции 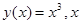 > 0, отсекающей от осей координат треугольник, площадь которого равна
> 0, отсекающей от осей координат треугольник, площадь которого равна  .
.
Инструкционная карта
ПР № 30 «Вычисление производных элементарных функций».
Задание:
1) Перепишите и заполните пропуски:
Пример 1. Найдите производные функций: а) y = ex – x 7 ,б) у=3ех+ cos 2 x, в) у = ех – sinx,
г) у=  – ln 2 x,д)
– ln 2 x,д)  , е)
, е)  , ж)
, ж) 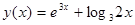
Решение: а)  б)
б)  в)
в)  = ех – cosx; г)
= ех – cosx; г)  ,
,
д)  е)
е)  ж)
ж) 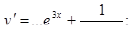
Ответ: а)  б)
б)  в)
в)  = ех – cosx; г)
= ех – cosx; г)  ,д)
,д) 
е)  ж)
ж) 
Пример 2. Вычислите значение производной функции:
а) у=  в точке
в точке  , б) у=ех sinx + x 2 в точке
, б) у=ех sinx + x 2 в точке  ,
,
в) у = cos 2 x + 4 x в точке  , г)
, г)  вточке
вточке  .
.
Решение: а)


б) 
в) 
г)  Ответ: а)10,5; б)1;в)4; г)2.
Ответ: а)10,5; б)1;в)4; г)2.
Пример 3. Найдите производные функций: а)  б)
б) 
в) 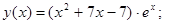 г)
г)  д)
д) 
Решение: а) у ¢ (x) = (x 2 + sin x)¢ = (x 2)¢ + (sin x)¢ = … x + cosx;
б) у ¢ (x) = (x 3 · cos x)¢ = (x 3)¢ · cos x + x 3 · (cos x)¢ = … x 2 · cos x + x 3· (− sin x) =
= x 2 · (3cos x − x · sin x),
в) у ¢ (x) = ((x 2 + 7 x − 7) · e x )¢ = (x 2 + 7 x − 7)¢ · e x + (x 2 + 7 x − 7) · (e x )¢ = (2 x + 7) · e x +
+(x 2 + 7 x − 7) · e x = e x · (2 x + 7 + x 2 + 7 x −7) = (x 2 + … x) · e x = x (x + …) · e x .
г) 
д) 
По традиции, разложим числитель на множители — это значительно упростит ответ:
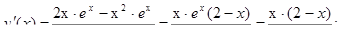
Ответ: а) у ¢ (x) = 2 x + cosx; б) у ¢ (x) = x 2 · (3cos x − x · sin x), в) у ¢ (x) = x (x + 9) · e x ,
г)  д)
д) 
Пример 4. Найти производные функций: f (x) = e 2 x + 3; g (x) = sin (x 2 + ln x).
Решение: Заметим, что если в функции f (x) вместо выражения 2 x + 3 будет просто x, то получится элементарная функция f (x) = e x . Поэтому делаем замену: пусть 2 x + 3 = t, f (x) = f (t) = e t . Ищем производную сложной функции по формуле:
f ¢ (x) = f ¢ (t) · t ¢ = (e t )¢ · t ¢ = e t · t ¢. Выполняем обратную замену: t = 2 x + 3. Получим:
f ¢ (x) = e t · t ¢ = e 2 x + 3 · (2 x + 3)¢ = e 2 x + 3 · 2 = … · e 2 x + 3
Теперь разберемся с функцией g (x). Очевидно, надо заменить x 2 + ln x = t. Имеем:
g ¢ (x) = g ¢ (t) · t ¢ = (sin t)¢ · t ¢ = cos t · t ¢. Обратная замена: t = x 2 + ln x. Тогда:
g ¢ (x) = cos (x 2 + ln x) · (x 2 + ln x)¢ = cos (x 2 + ln x) · (… x + 1/ x).
Ответ: f ¢ (x) = 2 · e 2 x + 3; g ¢ (x) = (2 x + 1/ x) · cos (x 2 + ln x).
Пример 5. Найти производную функции:
а)  б)
б) 
Решение: а) 

б) 
Ответ: а)  б)
б) 
2) Решить задание (по примерам):
1. Найдите производные функций: а) y = 2ex–3x7 ,б) у=5ех+cos3x, в) у = ех – cosx,
г) у=  –ln4х, д)
–ln4х, д)  , е)
, е)  , ж)
, ж) 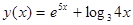
2. Вычислите значение производной функции:
а) у=  в точке
в точке  , б) у=2ех sinx +3 x2 в точке
, б) у=2ех sinx +3 x2 в точке  ,
,
в) у = cos2x + 8x в точке  ,г)
,г) 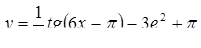 в точке
в точке  .
.
3. Найдите производные функций: а) 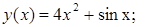 б)
б) 
в) 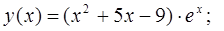 г)
г)  д)
д) 
4. Найти производные функций: f(x) = e 4x + 3; g(x) = sin (2x 2 + ln x).
5. Найти производные функций:а)  б)
б) 
3) Решить задание:
1. Найдите производную функции y = e - x – 2 x 7, у= 4х3+ е -х.
2. Найдите производную функции у = x 2 + sinx в точке х0 = p.
Найдите производную функции у = sin х ex – 9 x 3 в точке xo =0.
3. Найдите значение производной функции у = 5 cosx – 7 x в точке хо = 0.
4. Вычислите значение производной функции y = ln (2 x +11)+ 5 x вточке хо= – 5.
5. Найдите производную функции: а)  б)
б) 
Инструкционная карта
ПР № 31 «Исследование функции с помощью производной».
1) Перепишите и заполните пропуски:
Пример 1. Исследовать и построить график функции: 
Решение:
1. D (f) = R, т.к. f -многочлен.
2. Выясняем, является ли функция f четной или нечетной.  - функция ни четная, ни нечетная.
- функция ни четная, ни нечетная.
3. Функция непериодическая.
4. Находим точки пересечения графика с осями координат:
а) с осью ОХ: у=0 получаем точки (0;0), (3;0)
б) с осью ОУ: х=0 получаем точки (0;0)
5. Найдем производную функции: 
6. Найдем критические точки:  , т.е.
, т.е.  ,х= … или х=...
,х= … или х=...
Отмечаем эти точки 0 и 2 на числовой прямой, и определяем знак производной в каждом промежутке. − + −



 6(− 1)− 3(− 1)2= − 6− 3=− 9<0
6(− 1)− 3(− 1)2= − 6− 3=− 9<0
0 2 х
Значит, в промежутках  и
и  функция убывает и (0;2) – функция возрастает.
функция убывает и (0;2) – функция возрастает.
х=0 - точка минимума, т.к. производная меняет знак с минуса на плюс.
Вычислим уmin= 
х=2 – точка максимума, т.к. производная меняет знак с плюса на минус.
Вычислим уmax=  .
.
7.Составляем таблицу для внесения всех данных
| x | 
| 0 | (0;2) | 2 | 
|

| − | 0 | + | 2 | − |
| f (x) | 
| 0 | 
| 4 | 
|
| min | max |
|


|
|
|
|
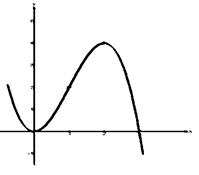
Пример 2. Сколько корней имеет уравнение: x4 − 4x3 − 9 = 0?
Решение: р (x) = x4 − 4x3 − 9, D(р) = (− 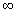 ;
; 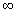 ).
).
р ' (x) = 4 x 3− 12x 2 = 4 x 2 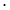 (х− 3) = 0, x1 = 0; 1 петля; x2 = …, р ' (4) = 4
(х− 3) = 0, x1 = 0; 1 петля; x2 = …, р ' (4) = 4  16
16  1> 0
1> 0
 | |||
| |||
р(x) убывает на интервале (– 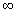 ; 3];р (x) возрастает на [3; +
; 3];р (x) возрастает на [3; + 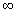 ).
).
x = 3 – min, р min= р (3) = 34 − 4  33 − 9 = 81− 4
33 − 9 = 81− 4  27 – 9 =81 − 117= − …< 0, в точке x = 0 график имеет точки перегиба (то есть меняет выпуклость), f(0) = 0 − 0 − 9 =...
27 – 9 =81 − 117= − …< 0, в точке x = 0 график имеет точки перегиба (то есть меняет выпуклость), f(0) = 0 − 0 − 9 =...
Строим эскиз графика

График пересекает ось 0Х в двух точках x1 и x2, следовательно, многочлен, а значит и данное уравнение имеет два корня.
Ответ: два.
Пример 3. Исследовать функцию f(x)= 3x5 − 5х3 + 2 и построим ее график.
Решение: 1.D (f) = R, так как f (x) - многочлен.
2.Функция f не является ни четной, ни нечетной, так как
f (− x) = 3(− x)5 − 5(− x)3 + 2 = − 3x 5 + 5х3 +
|
|
|


