 |
В) Преобразование выражений .
|
|
|
|
(Перепишите и заполните пропуски)



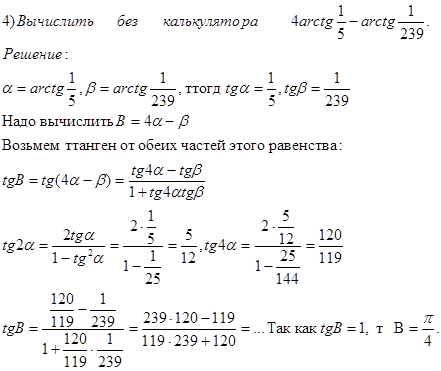


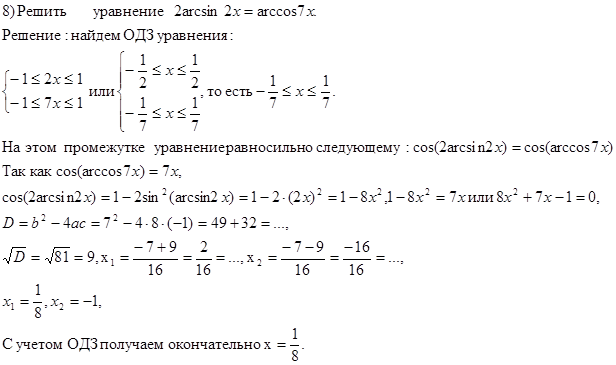
2) Решить задание (по примерам):



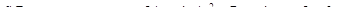


3) Решить задание:


В)1. Найдите значение выражения: а) arcsin1; б) arccos  ; в) arctg(
; в) arctg( ); г)arcctg0.
); г)arcctg0.
2. Найдите значение выражения: а) arcsin 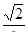 ; б) arccos0; в) arctg
; б) arccos0; в) arctg 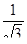 ; г) arcctg
; г) arcctg 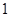 .
.
3.Выразите значения данных функций через значения функцииу=arcsinx:
а) arccos  ; б) arctg (
; б) arctg ( ); в) arcctg 2.
); в) arcctg 2.
4.Вычислите значения: a) cos  ; б)sin
; б)sin 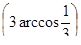 ; в) sin
; в) sin 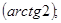
5. Упростите выражение: а) arctg  +arctg
+arctg  ; б) 3arcsin
; б) 3arcsin  +arcsin
+arcsin  .
.
6.Упростите выражение: а) arccos  б) - arcsin
б) - arcsin  ;
;
7. Найдите значение выражения: arcctg(ctg( 3)).
3)).
8. Найдите значение выражения:arcsin(sin(-6)).
9. Докажите справедливость раиенства: tg(2arccos 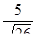
 arcsin
arcsin 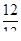 ) =
) =  .
.
10. Докажите справедливость раиенства: tg 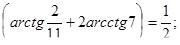

11. Решите уравнение: а)arccosx=  .б) arcsinx = 2arctg
.б) arcsinx = 2arctg  ; в)arctg(x-1)+
; в)arctg(x-1)+ 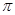 = 3arctg(x+1); г)
= 3arctg(x+1); г)  arcsin(x
arcsin(x 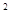
 x
x  2) = 0;
2) = 0;
12. Решите уравнение: а) arcsinx=  ;б) arcsinx = arcctgx; в) arccos(x+1) = arcctgx;
;б) arcsinx = arcctgx; в) arccos(x+1) = arcctgx;
г) 4arccos 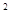 x
x  4
4 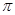 arccosx
arccosx  4
4  arcsinx+
arcsinx+  =0;д) arcsin(x +1) + arcos2x =0;
=0;д) arcsin(x +1) + arcos2x =0;
Инструкционная карта
ПР № 22 «Построение графиков функций с помощью преобразований».
Задание:
1) Опорный конспект.
Преобразования графиков функций — это линейные преобразования функции y = f (x) или её аргумента x к виду y = af (kx + b) + m, а также преобразование с использованием модуля.Зная, как строить графики функции y = f ( x ), где y = kx + b, y = ax2, y = xn , y=k/x,
y = sin x, y = cosx, y = tgx, y = ctgx, y=ax,y=logaxможно построить график функции y = af ( kx + b) + m.
|
|
|
| Общий вид функции | Преобразования |
| y = f (x - b) | Параллельный перенос графика вдоль оси абсцисс на| b |единиц
|
| y = f (x + b) |
|
| y = f (x) + m | Параллельный перенос графика вдоль оси ординат на| m |единиц
|
| Отражение графика | |
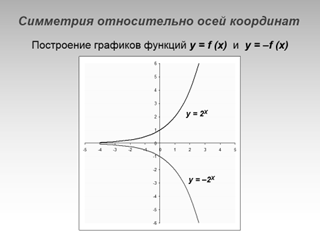
| y = f (- x) | Симметричное отражение графика относительно оси ординат. |
| y = - f (x) | Симметричное отражение графика относительно оси абсцисс. |
| Сжатие и растяжение графика | |
| y = f (kx) |
|
| y = kf (x) |
|
| Преобразования графика с модулем | |
| y = | f (x) | |
|
| y = f (| x |) |
|

Примеры построения функций.

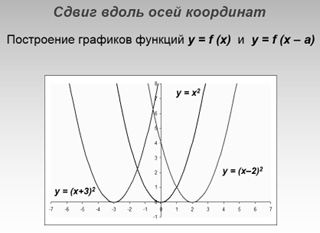





2) Решить задание:
1.

2.
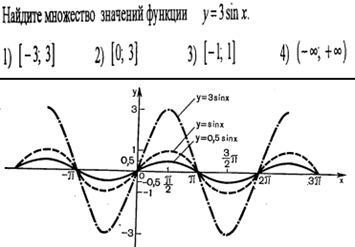
3.

4. 
5. 
6. 
7.

8. Построить графики функций:

9. Построить графики функций:1) у = 1/2 sin (3x) – 2, 2) y = 2× 3x+1 – 4,
3) y = 2 (x – 1)2 – 3, 4) y = –3 log2(x + 1), 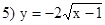 .
.
10.

Инструкционная карта
ПР № 23 «Решение уравнений с помощью графиков».
Задание:
1) Опорный конспект.
Графиком называется множество точек координатной плоскости, у которых значения x и y связаны некоторой зависимостью и каждому значению x соответствует единственное значение y.
Графический способ - один из самых удобных и наглядных способов представления и анализа информации.
На практике довольно часто оказывается полезным графический метод решения уравнений. Он заключается в следующем: для решения уравнений f(x)=0 строят график функции y=f(x) и находят абсциссы точек пересечения графика с осью Оx: эти абсциссы и являются корнями уравнения. Алгоритм решения уравнений графическим способом
|
|
|
Чтобы решить графически уравнение вида f(х) = g(х), нужно:
1.Построить в одной координатной плоскости графики функции:
у = f(х) и у = g(х).
2. Найти точки пересечения этих графиков.
3. Указать абсциссу каждой из этих пересечения.
4. Записать ответ.
 Довольно просто решать графически систему уравнений, так как каждое уравнение системы на координатной плоскости представляет какую- то линию.
Довольно просто решать графически систему уравнений, так как каждое уравнение системы на координатной плоскости представляет какую- то линию.
Построив графики этих уравнений и найдя координаты точек их пересечения (если они существуют), мы получим искомое решение.
Графическое решение неравенств, сводится к отысканию таких точек x, при которых один график лежит выше или ниже другого.
Примеры:
№ 1. Решите уравнение 

 № 2. Решите уравнение
№ 2. Решите уравнение 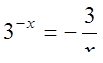
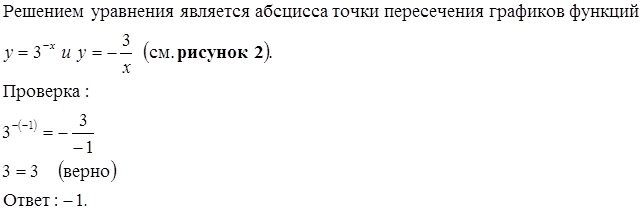
 №3. Решить уравнение
№3. Решить уравнение 
Решение: Построим графики функций  и y = x
и y = x
Графики функций не пересекаются, и, значит, уравнение не имеет корней (см. рисунок).
Ответ: корней нет.
 №4. Найти значение выражения х
№4. Найти значение выражения х  + у
+ у  ,если (х
,если (х  ;у
;у  ) является решением системы уравнений.
) является решением системы уравнений. 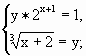
Решение:
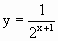
 -параллельный перенос на 1 единицу влево.
-параллельный перенос на 1 единицу влево.
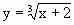 - параллельный перенос на 2 единицы влево.
- параллельный перенос на 2 единицы влево.
х  =-1, у
=-1, у  =1
=1
х  + у
+ у  =0.
=0.
Ответ: 0.
№5.Решите неравенство  >12 - 1,5х.№6.Решите неравенство
>12 - 1,5х.№6.Решите неравенство  . Oтвет: х>0.
. Oтвет: х>0.
 Ответ: х>2.
Ответ: х>2.

№7. Решить уравнение sinx+cosx=1. Построим графики функций y=sinx u y=1-cosx.(рисунок 5) Из графика видно, что уравнение имеет 2 решения: х=2πп,где пЄZ и х=π/2+2πk,где kЄZ.

 №8.Решить уравнение: 3x = (х-1) 2 + 3
№8.Решить уравнение: 3x = (х-1) 2 + 3
Решение: применяем функциональный метод решения уравнений:

 т.к. данная система имеет единственное решение, то методом подбора находим х=1
т.к. данная система имеет единственное решение, то методом подбора находим х=1
Ответ: 1.
№9.Решить неравенство: сos x  1 + 3x
1 + 3x
Решение:

 Ответ: (
Ответ: (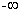 ;
;  ).
).
№10. Решить уравнение 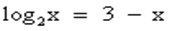
В нашем случае функция 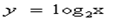 возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение
возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение 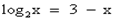 имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как
имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как  .
.
Ответ: 2.
2) Решить задание:
1)Есть ли корень у уравнения и если есть, то положительный он или отрицательный?


 а)
а) 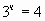 ; б)
; б)  , в) 6х =1/6, г)
, в) 6х =1/6, г)  .
.

2)Решить графическим методом уравнение  .
.
|
|
|
 3)Решитеграфическим методом уравнения:
3)Решитеграфическим методом уравнения:
а) 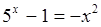 б)
б)  .
.
4)На рисунке изображен график функции
y = f (x). Найдите количество целых корней уравнения f (x)= 0.
1) 1 2) 6 3) 7 4) 8
5) На каком из рисунков изображен график функции  ?
?



 1) у 2) у 3) у 4) у
1) у 2) у 3) у 4) у
1 1 1

6) График какой функции изображен на рисунке?
1) у = 2х-1,5; 2) у = 2х – 2;
3) у = 2х – 3; 4) у = 2-х – 2.
7)График какой функции изображен на рисунке?

1) у = sinx; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
8)  На рисунке изображен график функций y
На рисунке изображен график функций y


 y = f (x) и y = g (x), заданный на промежутке
y = f (x) и y = g (x), заданный на промежутке
[-5;6]. Укажите те значения х, для которых
выполняется неравенство g (x)  f (x) 1
f (x) 1
1) [-5; 0] 2) [-5; 2]
0 1 x
 3) [-2; 2] 4) [2; 6]
3) [-2; 2] 4) [2; 6]
9)На рисунке изображен график функции
 y = f (x). Найдите количество целых корней уравнения f (x)= 0.
y = f (x). Найдите количество целых корней уравнения f (x)= 0.
1) 3 2) 4 3) 2 4) 1
10) На рисунке изображен график функции
y = f (x). Найдите количество целых корней уравнения f (x)+2= 0.
1) 3 2) 5 3) 4 4) 1

Инструкционная карта
ПР № 24 «Решение иррациональных уравнений».
Задание:
1) Перепишите и заполните пропуски:
Пример 1. Решить уравнение  Решение: Уединим радикал
Решение: Уединим радикал  Это уравнение равносильно системе
Это уравнение равносильно системе  Решим уравнение (1):
Решим уравнение (1): 

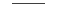
 х = … Найденное значение
х = … Найденное значение  удовлетворяет условиям (2) и (3).
удовлетворяет условиям (2) и (3).
Ответ: –1. Пример 2. а) Найдите корень уравнения 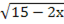 = 3. Решение: Возведем в квадрат правую и левую части уравнения:
= 3. Решение: Возведем в квадрат правую и левую части уравнения:  )2 = 32,15 – 2х = 9, –2х = 9 – 15, –2х = – 6, х =... Сделаем проверку. Для этого подставим число 3 в исходное уравнение:
)2 = 32,15 – 2х = 9, –2х = 9 – 15, –2х = – 6, х =... Сделаем проверку. Для этого подставим число 3 в исходное уравнение:  = 3, 3 = 3 – верно.
= 3, 3 = 3 – верно.
|
|
|
Ответ: 3.
б) Решить уравнение  =
=  .
.
Решение:  =
=  =>
=>  ˂=>
˂=>  =>
=> 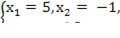 => х =...
=> х =...
Ответ: – 1. Пример 3. Решить уравнение  = х -7.
= х -7.
Решение:  = х -7 =>
= х -7 =>  =>
=>  =>
=>  =>
=>  => х =...
=> х =...
Ответ: 14.
Пример 4. Решите уравнение 
 =
=  .
.
Решение: 
 =
=  => 7
=> 7  х + х
х + х  2
2  2
2  = 2х
= 2х  5 =>
5 =>
5 – х =  => 25 – 10х + х2 =
=> 25 – 10х + х2 =  х2 + 9х – 14 => 2х2
х2 + 9х – 14 => 2х2  19х + 39 = 0,
19х + 39 = 0,
D = (– 19)2  4
4  2
2  39= 361 – 312 = …, х1= (19 + 7): 4 = …, х2 = (19 – 7): 4 = …,
39= 361 – 312 = …, х1= (19 + 7): 4 = …, х2 = (19 – 7): 4 = …,
Проверка: а) х1= 6,5,  –
–  =
=  ,
,

 =
=  – неверное равенство.
– неверное равенство.
б) х2 = 3, 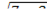 –
–  =
=  ,
, 
 =
=  , – верное равенство.
, – верное равенство.
Ответ: 3.
Пример 5. Решить уравнение 
Решение: Возводим в куб обе части уравнения  получим
получим  Учитывая, что выражение в скобках равно 1 (см. условие), получаем
Учитывая, что выражение в скобках равно 1 (см. условие), получаем 

 Возводим в куб:
Возводим в куб: 

 Проверкой убеждаемся, что
Проверкой убеждаемся, что  и
и 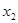 корни уравнения.
корни уравнения.
Ответ: 80, – 109.
2) Решить задание (по примерам):
Решить уравнения:
1. 
2. а)  . б)
. б) 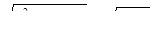 .
.
3.  .
.
4. 
5. 
3) Решить задание:
1. Решить уравнение:  .
.
2. Решить уравнение:  .
.
3. Решить уравнение: 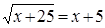 .
.
4. Решить уравнение:  .
.
5. Решить уравнение:  .
.
6. Решить уравнение:3  .
.
7. Решить уравнение:  .
.
8. Решить уравнение: 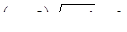 .
.
9. Решить уравнение:  .
.
10. Решить уравнение:  .
.
11. Найдите корень уравнения: 
12. Найдите корень уравнения: 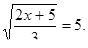
13. Найдите корень уравнения: 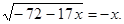
Если уравнение имеет более одного корня, укажите меньший из них.
14. Найдите корень уравнения: 
15. Найдите корень уравнения: 
16. Решить уравнение: 
17. Решить уравнение: 
18. Решить уравнение: 
19. Решить уравнение: 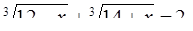
20. Решить уравнение: 
21. Решить уравнение: 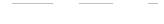
22. Решить уравнение: 
23. Решить уравнение: 
24. Решить уравнение: 
25. Решить уравнение: 
Инструкционная карта
ПР № 25 «Решение показательных уравнений».
Задание:
1) Перепишите и заполните пропуски:
Пример 1. а) Найдите корень уравнения 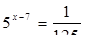 .
.
Решение: Чтобы решить это уравнение, вспомним свойства степени и приведем правую и левую части уравнения к степени с основанием 5:  ,
,
Если степени с равными основаниями равны, то равны их показатели. Приравняем показатели степеней: х – 7 = - 3, х = 7 – 3, х =...
Ответ: 4.
б)Найдите корень уравнения  .
.
Решение: Представим правую и левую части уравнения в виде степени с основанием 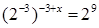 ,
,
Приравняем показатели степеней: –3  (–3+ х) = 9, 9 – 3х = …, –3х = 0, х =...
(–3+ х) = 9, 9 – 3х = …, –3х = 0, х =...
Ответ: 0.
Пример 2. Решите уравнение  .
.
Разделим обе части уравнения на  :
:  .
.
Пусть 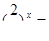 m,m> 0, тогда 2m2 – 3m – 5 = 0, D = 9 – 4
m,m> 0, тогда 2m2 – 3m – 5 = 0, D = 9 – 4  2
2  (– 5) = 9 + 40 = …, m1 = (3 + 7): 4 = …,
(– 5) = 9 + 40 = …, m1 = (3 + 7): 4 = …,
|
|
|
m2 = (3 – 7): 4 = – 4: 4 = …, – не удовл. условию m> 0.
Если m = 2,5, то 
Ответ: – 1.
Пример 3. Решите уравнение 49x  8∙7x + 7 = 0.
8∙7x + 7 = 0.
Решение: Обозначим 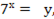 получим уравнение относительно у: у2 – 8у + 7 = 0,
получим уравнение относительно у: у2 – 8у + 7 = 0,
D = (–8)2  4
4  1
1  7= 64 – 28 = …, у1= (8 + 6): 2 = …, у2 = (8 – 6): 2 =... Получим, что
7= 64 – 28 = …, у1= (8 + 6): 2 = …, у2 = (8 – 6): 2 =... Получим, что  и
и  , отсюда х1 = …, х2 =... Ответ: х1 = 1, х2 = 0.
, отсюда х1 = …, х2 =... Ответ: х1 = 1, х2 = 0.
Пример 4. а)Решить уравнение  .
.
Решение: 
Ответ: 3.
б) Решите уравнение 
Решение: 
Ответ: 1.
в)Решите уравнение 
Решение: 
Ответ: 4.
Пример 5. Решите уравнение а) 2х+1 + 2х-1 + 2х = 28, б) 9х – 8∙3х – 9 = 0, в) 8∙4х – 6∙2х + 1 = 0.
Решение:
а) 2х+1 + 2х-1 + 2х = 28, 2х-1 ∙ (22 + 1 + 2) = 28, 2х-1∙7 = 28, 2х-1 = 4, 2х-1 = 22, х – 1 = 2, х =...
Ответ: 3.
б) 9х – 8∙3х – 9 = 0, (3х)2 – 8∙3х -9 = 0, Обозначим 3х = t, где t >0, тогда t2 – 8t – 9 = 0,
D = (–8)2  4
4  1
1  (–9) = 64 + 36 = …, t 1= (8 + 10): 2 = …, t 2 = (8 – 10): 2 =.... t1 = 9, t2 = –1, Возвращаемся к замене: 3х = 9, х = …, 3х = –1, корней нет.
(–9) = 64 + 36 = …, t 1= (8 + 10): 2 = …, t 2 = (8 – 10): 2 =.... t1 = 9, t2 = –1, Возвращаемся к замене: 3х = 9, х = …, 3х = –1, корней нет.
Ответ: 2.
в) 8∙4х – 6∙2х + 1 = 0, 8∙(2х)2 – 6∙2х + 1 = 0, Обозначим 2х = t, где t >0, тогда 8 t2 – 6t + 1 = 0, D = (–6)2  4
4  1
1  8= 36 – 32 = …, t1= (6 + 2): 16 = …, t2 = (6 – 2): 16 =... t1 =
8= 36 – 32 = …, t1= (6 + 2): 16 = …, t2 = (6 – 2): 16 =... t1 =  , t2 =
, t2 =  Возвращаемся к замене: 2х =
Возвращаемся к замене: 2х =  , х 1= …, 2х =
, х 1= …, 2х =  , х 2=...
, х 2=...
Ответ: – 1, – 2.
2) Решить задание (по примерам):
1. а) Найдите корень уравнения  . б) Найдите корень уравнения:
. б) Найдите корень уравнения:  .
.
2. Решите уравнение  .
.
3. Решите уравнение 25x  6∙5x + 5 = 0.
6∙5x + 5 = 0.
4. а)Решить уравнение: 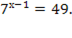 б)Решите уравнение
б)Решите уравнение 
в)Решите уравнение  .
.
5. Решите уравнение а) 3х+1 + 3х-1 + 3х = 117, б) 16х – 15∙4х – 16 = 0, в) 81х + 6∙9х + 9 = 0.
3) Решить задание:
1. Решить уравнения: а)  , б)
, б)  в)
в) 
2. Решите уравнение а) 4x  5∙2x + 4 = 0, б) 9x
5∙2x + 4 = 0, б) 9x  4∙3x + 3 = 0.
4∙3x + 3 = 0.
3. Решитеуравнение 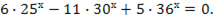
4. Найдите сумму корней уравнения: 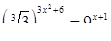 .
.
5. Если  - корень уравнения
- корень уравнения  , то найдите значение выражения
, то найдите значение выражения  .
.
6. Найдите произведение корней уравнения  .
.
7. Решите уравнение  .
.
8. Решите уравнение 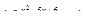 .
.
9. Решите уравнение 
10. Решите уравнение 4х+2х – 6=0;
11. Решите уравнение 9х+3х+1=4;
12. Решите уравнение 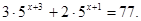
13. Решите уравнение 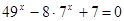 .
.
14. Решите уравнение:  .
.
15. Решите уравнение: 92х+1 – 92х= 72.
16. Решите уравнение: 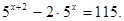
17. Пусть х 0 ─ наибольший корень уравнения  . Найти 2 х 0 – 5.
. Найти 2 х 0 – 5.
18. Решите уравнение: 23х+2 + 8х = 0,625.
19. Пусть х 0 ─ наименьший корень уравнения 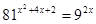 . Найти 3 х 0 + 2.
. Найти 3 х 0 + 2.
20. Найти сумму корней уравнения: 4х – 40∙2х + 256 = 0.
21. Решите уравнение: 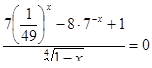
22. Решите уравнение:3 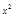 ∙
∙  + 325 ∙
+ 325 ∙  = 0.
= 0.
23. Решите уравнения:

24. Решите уравнения: 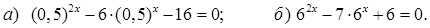
25. Решите уравнение:  .
.
26. Решите уравнения:
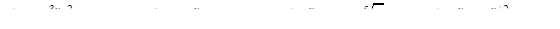
27. Решите уравнение: 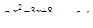 .
.
28. Решите уравнения: 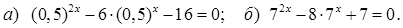
29. Найти корень (или сумму корней, если их несколько) уравнения: 7 · 8х+1 + 8х+3 = 71.
30. Найти корень (или сумму корней, если их несколько) уравнения: 72х = 6 · 7х + 7.
31. Решите уравнение:  .
.
32. Решите уравнение:  .
.
Инструкционная карта
ПР № 2 6 «Решение логарифмических уравнений».
Задание:
1) Перепишите и заполните пропуски:
Пример 1. Решите уравнение  Решение: Используем метод - решение логарифмических уравнений заменой.
Решение: Используем метод - решение логарифмических уравнений заменой.
ОДЗ: х > 0. Введем замену  , чтобы записать исходное уравнение в виде стандартного квадратного уравнения. Тогда уравнение примет вид: у2 – 4у + 4 = 0, (у – 2)2 = 0, у – 2 = 0, у =... Вернемся к х:
, чтобы записать исходное уравнение в виде стандартного квадратного уравнения. Тогда уравнение примет вид: у2 – 4у + 4 = 0, (у – 2)2 = 0, у – 2 = 0, у =... Вернемся к х: 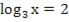 . Тогда по определению логарифма получаем, что х = 32, х = … - уд.ОДЗ.
. Тогда по определению логарифма получаем, что х = 32, х = … - уд.ОДЗ.
Ответ: 9.
Пример 2. Решите уравнение:  .
.
Решение: Вновь начнем решение с определения области допустимых значений уравнения. Она определяется следующей системой неравенств: 
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению: 
Основания логарифмов одинаковы, поэтому в области допустимых значений можно перейти к следующему квадратному уравнению:
(х + 2)  (х + 3) = 1
(х + 3) = 1  х, х2 + 6х + 5 = 0, D = (6)2
х, х2 + 6х + 5 = 0, D = (6)2  4
4  1
1  5= 36 – 20 = …,
5= 36 – 20 = …,
х1= ( 6
6  4): 2 =
4): 2 =  , х2 = (
, х2 = ( 4): 2 =
4): 2 =  ...
...
Первый корень не входит в область допустимых значений уравнения, второй — входит.
Ответ: x = -1.
Пример 3. Решите уравнение: 
Решение: Найдем ОДЗ по определению логарифма. ОДЗ:
 .
.
Перепишем исходное уравнение, используя свойства суммы логарифмов и логарифма степени. Получим следующее уравнение: 
Приравняем подлогарифмические выражения:
(3х 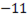 )
)  (х
(х  ) =
) =  ,
, 
Найдем корни полученного квадратного уравнения:
D = ( 92)2
92)2  4
4  1
1  (
(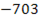 ) = 8464 + 8436 = …,
) = 8464 + 8436 = …,
х1= (92 + 130): 6 = 222: 6 = …, х2 = (92


