 |
Т Е С Т по теме «Перпендикулярность плоскостей».1 часть. 7 глава
|
|
|
|

2. Решите уравнения:

3. Решите уравнения:
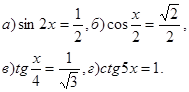
4. Решите уравнения:

5. Решите уравнения: 
6. Решите уравнения:
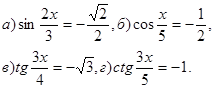
7. Решите уравнения: 
8. Решите уравнения: 
9. Решите уравнения: 
10. Решите уравнения: 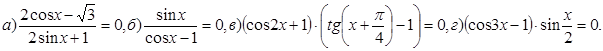
11. Решите уравнения:
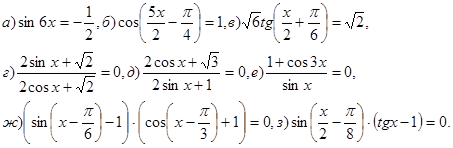
12. Решите уравнения:

13. Решите неравенства: а)  ,б)
,б)  , в)
, в) 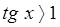 .
.
14. Решите неравенства:
а)  ;б)
;б) 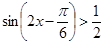 ;в)
;в)  ;
;
15. Найдите какой-либо корень уравнения  , удовлетворяющий неравенству
, удовлетворяющий неравенству 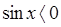 .
.
16. Решите неравенство:  .
.
Решите неравенство:

Решите неравенства:
а) 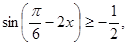 б)
б) 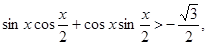 в)
в)  .
.
19. Решите неравенства:
а) 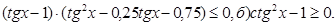
20. Определите все а, при каждом из которых неравенство
4sinx + 3cosx ≤ а имеет хотя бы одно решение.
Инструкционная карта
ПР № 11 «Вычисление обратных тригонометрических выражений».
Задание:
1) Перепишите и заполните пропуски:
Для выполнения заданий, связанных с обратными тригонометрическими функциями, нужно, во-первых, четко помнить определения этих понятий:
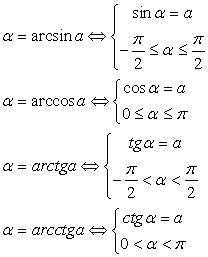

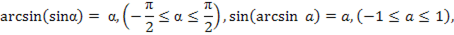

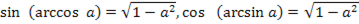 ,
,


Пример 1. Вычислить:
а)arccos (cos  ), б) cos(arccos 0,4),в) arcsin (sin
), б) cos(arccos 0,4),в) arcsin (sin  ),
),
г) sin(arcsin 0,6),д) sin (arccos 0,6),е)tg(arcsin 0,8).
Решение:
а)arccos (cos  ) =
) =  , б) cos(arccos 0,4) = …,
, б) cos(arccos 0,4) = …,
в) arcsin (sin  ) =…, г) sin(arcsin 0,6) = 0,6,
) =…, г) sin(arcsin 0,6) = 0,6,
д) 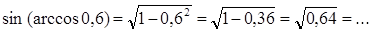 ,
,
е)  .
.
Ответ:
а)arccos (cos  ) =
) =  , б) cos(arccos 0,4) = 0,4,в) arcsin (sin
, б) cos(arccos 0,4) = 0,4,в) arcsin (sin  ) =
) =  ,
,
г) sin(arcsin 0,6) = 0,6, д) 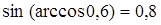 , е)
, е) 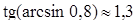 .
.
Пример 2. Вычислить cos(4arctg 5).
Решение:
Пусть α = arctg5, тогда tg α = 5. Требуется найти cos4α. Вычислим вначале cos2α, используя универсальную подстановку:
 .
.
Тогда получаем, что:
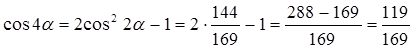 .
.
Ответ:  .
.
Пример 3. Вычислить arcsin (sin 12).
Решение:
По условию задачи требуется найти угол, синус которого равен синусу угла в 12 радиан и который принадлежит промежутку  Заметим, что
Заметим, что 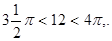 поэтому
поэтому 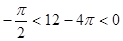 .Поскольку
.Поскольку 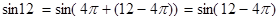 , угол 12 - 4π является искомым углом: его синус равен sin 12, и он находится в области возможных значений арксинуса.
, угол 12 - 4π является искомым углом: его синус равен sin 12, и он находится в области возможных значений арксинуса.
Ответ: arcsin (sin12) = 12 - 4π.
Пример 4. Вычислить 
Решение:
|
|
|
Введем два угла: 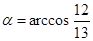 и
и  . Оба они лежат в первой четверти, значит, все их тригонометрические функции положительны.
. Оба они лежат в первой четверти, значит, все их тригонометрические функции положительны.
Мы знаем, что 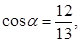
 . Требуется найти синус суммы этих углов, а для этого нужно знать их синусы и косинусы.
. Требуется найти синус суммы этих углов, а для этого нужно знать их синусы и косинусы.
Во-первых,
 .
.
Во-вторых,
 .
.
Следовательно, 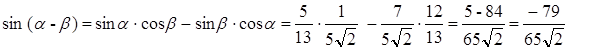
Ответ:  .
.
Пример 5. Вычислить 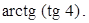
Решение:
Типичная ошибка в данном случае – это сразу же написатьв ответ 4. Как мы указывали в предыдущем примере, для использования основных свойств аркфункций необходимо проверить соответствующие ограничения на их аргумент. Мы имеем дело со свойством:
 при
при 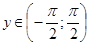 .Но 4>
.Но 4> 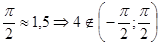 .
.
Главное на этом этапе решения не подумать, что указанное выражение не имеет смысла и его нельзя вычислить. Ведь четверку, которая является аргументом тангенса, мы можем уменьшить при помощи вычитания периода тангенса, и это не повлияет на значение выражения. Проделав такие действия, у нас появится шанс уменьшить аргумент так, чтобы он вошел в указанный диапазон.
 , т.к.
, т.к.  < 1 поскольку
< 1 поскольку  > 3, следовательно,
> 3, следовательно, 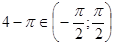 , т.к.
, т.к. 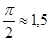 .
.
Ответ:  .
.
Пример 6. Вычислить sin (2 arcsin 0,6).
Решение:

Ответ: 0,96.
Пример 7. Вычислитьarccosx – arcsinx = arccos 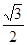 .
.
Решение:
Учитывая, что arccos  =
=  и arcsinx + arccosx =
и arcsinx + arccosx = 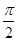 , заменим в уравнении arcsinx выражением
, заменим в уравнении arcsinx выражением 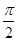 – arccosx, получим уравнение
– arccosx, получим уравнение
arccos x – (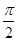 – arccos x)=
– arccos x)=  ,
,
2arccos x – 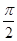 =
= 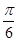 , 2arccos x =
, 2arccos x = 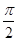 +
+ 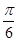 =
=  .
.
arccos x =  , x = cos
, x = cos  , x= 1/2 = …
, x= 1/2 = …
Ответ: 0,5.
Пример 8. Решите уравнения:
а) 6arcsin (x2 – 6x+8,5) = π;
б) 3arcsin2x – 10arcsinx + 3 = 0.
Решение:
а)6arcsin (x2 – 6x+8,5) = π, arcsin(x2 – 6x+8,5) =  ,
,
x2 – 6x+8,5 = 0,5; x2 – 6x+8 = 0,
D = 36 – 4  1
1  8 =….
8 =….
 ,
,  .
.
б) 3arcsin2x – 10arcsinx + 3 = 0. arcsinx = у, 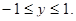
3у2 – 10у + 3 = 0, D = 100 – 4  3
3  3 = 64.
3 = 64.
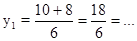 - не уд. усл.
- не уд. усл. 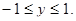
 .
.
arcsinx = 0,3, х= sin 0,3
Ответ: а) x1= 4,x2 = 2.б) х= sin 0,3
Пример 9. Вычислить: а) arcsin (-2), б) arccos 
Решение:
а) Типичная ошибка в данном случае – это начать выносить минус и что-то упрощать. Первое, что необходимо заметить, это то, что аргумент арксинуса не входит в область определения  .
.
|
|
|
Следовательно, данная запись не имеет значения, и вычислить арксинус нельзя.
б) Стандартная ошибка в данном случае заключается в том, что путают местами значения аргумента и функции и дают ответ 1/2. Это неверно! Конечно, возникает мысль, что в таблице косинусу  соответствует значение 1/2, но в таком случае перепутано то, что вычисляются аркфункции не от углов, а от значений тригонометрических функций. Т.е. arccos 1/2 =
соответствует значение 1/2, но в таком случае перепутано то, что вычисляются аркфункции не от углов, а от значений тригонометрических функций. Т.е. arccos 1/2 =  , а неarccos
, а неarccos  = 1/2.
= 1/2.
Кроме того, поскольку мы выяснили, что  является именно аргументом арккосинуса,
является именно аргументом арккосинуса,
то необходимо проверить, чтобы он входил в область определения. Для этого вспомним, что  >1,т.е.
>1,т.е.  , а значит арккосинус не имеет смысла и вычислить его нельзя.
, а значит арккосинус не имеет смысла и вычислить его нельзя.
Кстати, например, выражениеarccos  имеет смысл, т.к.
имеет смысл, т.к.  , но поскольку значение косинуса, равное
, но поскольку значение косинуса, равное  не является табличным, то и вычислить арккосинус с помощью таблицы нельзя.
не является табличным, то и вычислить арккосинус с помощью таблицы нельзя.
Ответ: Выражения не имеют смысла.
Пример 10. Вычислить arcсtg х, если известно, чтоarctg х =  .
.
Решение:
Вспомним, по какой формуле связаны между собой указанные функции:

И выразим из нее то, что нам нужно: 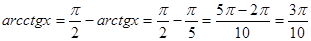 .
.
Ответ:  .
.
2) Решить задание (по примерам):
1. Вычислить:
а)arccos (cos  ), б) cos(arccos 0,25),в) arcsin (sin
), б) cos(arccos 0,25),в) arcsin (sin 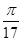 ),
),
г) sin(arcsin 0,45), д) sin (arccos 0,8),е)tg(arcsin 0,6).
2. Вычислить cos(4arctg 3).
3. Вычислить arcsin (sin 6).
4. Вычислить 
5. Вычислить 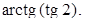
6. Вычислить sin (2 arcsin 0,8).
7. Вычислить arccos x – arcsin x =  arccos
arccos  .
.
8. Решите уравнения:
а) 6arcsin (x2 – 7x+12,5) = π;
б) 3arcsin2x – 11arcsinx + 6 = 0.
9. Вычислить: а) arcsin( 4), б) arccos
4), б) arccos 
10. Вычислить arcсtg х, если известно, чтоarctg х =  .
.
Инструкционная карта
ПР № 12 «Вычисление и сравнение корней. Выполнение расчетов с радикалами».
Задание:
1) Перепишите и заполните пропуски:
Пример 1. Вычислите: 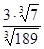 . Решение:
. Решение:  .
.
Ответ: 1.
Пример 2. Вычислите:  .
.
Решение: 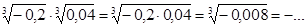 .
.
Ответ:  0,2.
0,2.
Пример 3. Упростите выражение:  .
.
Решение: 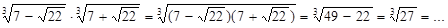 .
.
Ответ: 3.
Пример 4. Вычислите: а)  б)
б) 
в) 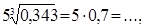 г)
г)  д)
д) 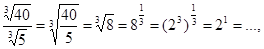
е)  ж)
ж) 
з) 
Ответ: а) 6, б)  8, в) 3,5; г) 40, д) 2, е) 10, ж) 1,25; з) 250.
8, в) 3,5; г) 40, д) 2, е) 10, ж) 1,25; з) 250.
Пример 5. Выполнить действия: 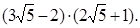 Решение:
Решение:  Ответ:
Ответ: 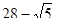
Пример 6. Решите уравнения: 
Решение: 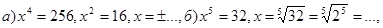 Ответ: а)х =
Ответ: а)х =  4, б) х = 2.
4, б) х = 2.
Пример 7. а) Вынести множитель из-под знака корня:  ,
,
 внесите множитель под знак корня:
внесите множитель под знак корня:  .
.
|
|
|
Ответ: а)  б)
б)  .
.
2) Решить задание (по примерам):
1. Вычислите: 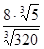 .
.
2. Вычислите:  .
.
3. Упростите выражение: 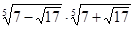 .
.
4. Вычислите:
а) 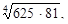 б)
б)  в)
в) 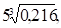 г)
г) 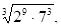 д)
д) 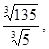
е)  ж)
ж)  з)
з) 
5. Выполнить действия: 
6. Решите уравнения: 
7. а) Вынести множитель из-под знака корня:  ,
,
 внесите множитель под знак корня:
внесите множитель под знак корня:  .
.
3) Решить задание:
1. Вычислите: а) 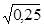 ,б)
,б)  ,в)
,в) 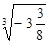 ,г)
,г)  ,д)
,д)  ,
,
е)  ,ж)
,ж) 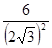 , з)
, з)  .
.
2. Решите уравнения: а) 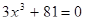 , б)
, б)  , в)
, в) 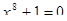 , г)
, г) 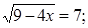
3. Упростите выражение:  .
.
4. Вычислите: а) 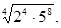 б)
б) 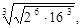 в)
в) 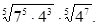
5. а) вынести множитель из-под знака корня: 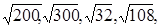
б) внесите множитель под знак корня: 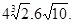
6. Вычислите а) 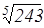 ,б)
,б) 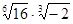 ,в)
,в)  г)
г)  ,д)
,д) 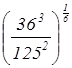 .
.
7. Упростите выражение 
8. Найдите значения выражения  при у = 16.
при у = 16.
9. Найдите значение выражения: 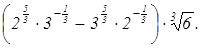
10. Сократите дробь: 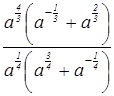 .
.
11. Найдите значения выражения  при а = 4, b = 5.
при а = 4, b = 5.
12. Найдите значение выражения 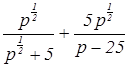 при р = 49.
при р = 49.
13. Упростите выражение  .
.
14. Упростите выражение 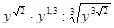 .
.
15. Вычислите 
16. Упростите выражение  .
.
17. Найдите значение выражения: 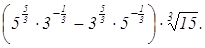
18. Найдите значение выражения: 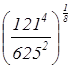 .
.
19. Упростите выражение  .
.
20. Упростите выражение 
Инструкционная карта
ПР № 13 «Нахождение значений степеней с рациональными показателями. Сравнение степеней».
Задание:
1) Перепишите:
Определение. Степенью числа  с рациональным показателем
с рациональным показателем  , где m-целое число, а n-натуральное (
, где m-целое число, а n-натуральное ( ), называется число
), называется число  . Итак, по определению
. Итак, по определению 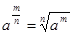 .
.
|
|
|


