 |
Т Е С Т по теме «Перпендикулярность плоскостей».1 часть. 4 глава
|
|
|
|
45. №8. а) Сколько двузначных чисел можно составить из цифр 1, 3, 5, 7, 9?
б) Сколько среди них чисел, кратных 5? в) Сколько среди них чисел, кратных 3?
Инструкционная карта
ПР № 6 «Вычисление вероятностей».
Задание:
1) Перепишите и заполните пропуски:
Пример 1. a)В партии из 100 деталей имеется 5 бракованных. Определить вероятность того, что, взятая наугад, деталь окажется стандартной.
Решение: А: взятая наугад деталь оказалась стандартной.
Число исходов, благоприятствующих наступлению события А, равно 95.Поэтому вероятность события равна P(A) = m/ n = 95/100 = ….  Ответ: 0,95.
Ответ: 0,95.
б) Из пяти букв разрезной азбуки составлено слово «книга». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получится слово «книга».
Решение: А: из рассыпанных букв сложится слово «книга»
Число всех возможных исходов равно n = Pn = 5! = 120.
Число исходов, благоприятствующих событию А равно m =1.
Вероятность события А равна P(A) = m/ n = 1/120 = …. 
Ответ: 0,0083.
Пример 2. a) В коробке лежат 8 зеленых, 7 синих и 15 красных карандашей. Вычислить вероятность того, что взятый наугад карандаш будет, синим или зеленым.
Решение: А: взяли синий карандаш, В: взяли зеленый карандаш, С: взяли синий или зеленый карандаш. Событие С равно сумме событий А и В: С = А + В
Вероятность события А равна P(A) = m/ n = 7/30.
Вероятность события В равна P(B) = m/ n = 8/30.
Вероятность события С равна P(C) = P(A) 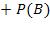 = 7/30
= 7/30  8/30 = 15/30 =...
8/30 = 15/30 =...
Ответ: 0,5. б) В урне лежат шары, двузначные номера которых составлены из цифр 1,2,3,4,5. Какова вероятность вынуть шар с номером 15? Решение: А: вынут шар с номером 15.
|
|
|
Число всех возможных исходов равно n = 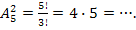
Число исходов, благоприятствующих событию А, m = 1.
Вероятность события А равна P(A) = m/ n = 1/20 = ….
Ответ: 0,05.
Пример 3. a) Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наугад. Найти вероятность того, что набраны нужные цифры.
Решение: А: абонент наугад набрал нужные цифры.
Число всех возможных исходов равно n = 
Число исходов, благоприятствующих событию А, m = 1
Вероятность события А равна P(A) = m/ n = 1/90 =....
Ответ: 0,011.
б)Устройство содержит два независимо работающих элемента. Вероятности отказа элементов равны соответственно 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
Решение: Пусть событие А — «устройство не работает», В1 — «отказал первый элемент»,
В2 — «отказал второй элемент».Событие А соответствует тому, что может отказать один из «цементов либо оба элемента. События В1 и В2 независимы в совокупности, поэтому:
q1 = 1 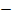 0,05 = 0,95, q2 = 1
0,05 = 0,95, q2 = 1 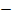 0,08 = 0,92. P(A) = 1
0,08 = 0,92. P(A) = 1 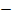 q1
q1 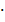 q2= 1
q2= 1 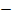 0,95
0,95 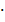 0,92 = 1
0,92 = 1  0,874 =...
0,874 =...
Ответ: 0,126.
Пример 4. a)Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
Решение: Пусть p - вероятность попадания в цель при одном выстреле. Введем событие
X = {при четырех выстрелах есть хотя бы одно попадание} и противоположное ему событие
 = {при четырех выстрелах нет ни одного попадания}.
= {при четырех выстрелах нет ни одного попадания}.
Вероятность события  равна P(
равна P( ) = (1
) = (1 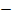 p)4, тогда вероятность события Х равна
p)4, тогда вероятность события Х равна
|
|
|
P(X) =1 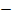 P(
P(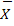 ) = 1
) = 1 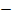 (1
(1 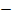 p)4. По условию эта вероятность равна 0,9984, откуда получаем уравнение относительно p: 1
p)4. По условию эта вероятность равна 0,9984, откуда получаем уравнение относительно p: 1 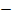 (1
(1 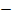 p)4 = 0,9984,(1
p)4 = 0,9984,(1 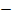 p)4 = 0,0016,(1
p)4 = 0,0016,(1 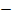 p) = 0,2,p =...
p) = 0,2,p =...
Таким образом, вероятность попадания в цель при одном выстреле равна 0,8.
Ответ: 0,8.
б)На полке в случайном порядке расставлено 40 книг, среди которых находится трехтомник Пушкина. Найти вероятность того, что эти тома стоят в порядке возрастания номера слева направо, но не обязательно рядом.
Решение: Используем классическое определение вероятности: P = m/n, где n- число всех равновозможных элементарных исходов, m - число элементарных исходов, благоприятствующих осуществлению события A = (Тома стоят в порядке возрастания номера слева направо, но не обязательно рядом). n= 40⋅39⋅38 =59280, так как первый том можно поставить на любое из 40 мест, второй - на любое из 39 мест и третий - на любое из оставшихся 38 мест.
А число m= 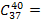 40! / (37!
40! / (37! 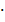 3!) = (40⋅39⋅38): (1⋅2⋅3) =...
3!) = (40⋅39⋅38): (1⋅2⋅3) =...
Тогда искомая вероятность P(A)= m/n = 9880/59280 = 1/6.
Ответ: 1/6.
Пример 5. а)В коробке имеется 250 лампочек, из них 100 по 90Вт, 50 - по 60Вт, 50 - по 25Вт и 50 – по 15Вт. Определить вероятность того, что мощность любой наугад взятой лампочки не превысит 60Вт.
Решение: 1. Рассматриваем следующие события: А = {мощность лампочки равна 90Вт}, вероятность Р(А) = 100/250 = 0,4; В = {мощность лампочки равна 60Вт}; С = {мощность лампочки равна 25Вт}; D = {мощность лампочки равна 15Вт}.
2. События А, В, С, D образуют полную систему, так как все они несовместны и одно из них обязательно наступит в данном опыте (выборе лампочки). Вероятность наступления одного из них есть достоверное событие, тогда Р (А)  Р (В)
Р (В)  Р (С)
Р (С)  Р (D) = 1.
Р (D) = 1.
3. События {мощность лампочки не более 60Вт} (т.е. меньше или равна 60Вт), и {мощность лампочки более 60Вт} (в данном случае – 90Вт) являются противоположными. По свойству противоположных чисел Р (В)  Р (С)
Р (С)  Р (D) = 1
Р (D) = 1 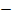 Р (А).
Р (А).
4. Учитывая, что Р (В)  Р (С)
Р (С)  Р (D) = Р (В
Р (D) = Р (В 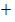 С
С 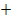 D), получим
D), получим
Р (В 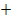 С
С 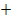 D) = 1
D) = 1 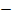 Р (А) = 1
Р (А) = 1 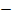 0,4 =... Ответ: 0,6.
0,4 =... Ответ: 0,6.
б) Вероятность поражения цели первым стрелком при одном выстреле равна 0,7, а вторым стрелком – 0,9. Найти вероятность того, что
1) цель будет поражена только одним стрелком; 2) цель будет поражена хотя бы одним стрелком.
Решение: 1. Рассматриваем следующие события:
А1 = {первый стрелок поражает цель}, Р (А1) = 0,7 из условия задачи;
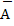 1 = {первый стрелок промахнулся}, при этом Р (А1)
1 = {первый стрелок промахнулся}, при этом Р (А1) 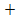 Р (
Р (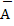 1) = 1, поскольку А1 и А̄1 – противоположные события. Отсюда Р (
1) = 1, поскольку А1 и А̄1 – противоположные события. Отсюда Р (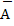 1) = 1
1) = 1 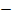 0,7 = …;
0,7 = …;
А2 = {второй стрелок поражает цель}, Р (А2) = 0,9 из условия задачи;
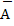 2 = {второй стрелок промахнулся}, при этом Р (
2 = {второй стрелок промахнулся}, при этом Р ( 2) = 1
2) = 1 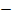 0,9 = …
0,9 = …
|
|
|
2. Событие А={цель поражена только одним стрелком} означает, что наступило одно из двух несовместных событий: либо А1 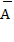 2, либо
2, либо 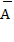 1А2.
1А2.
По правилу сложения вероятностей Р (А) = Р (А1 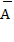 2) + Р (
2) + Р (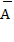 1А2).По правилу умножения вероятностей независимых событий:
1А2).По правилу умножения вероятностей независимых событий:
Р (А1 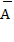 2) = Р (А1)
2) = Р (А1)  Р (
Р (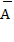 2) = 0,7
2) = 0,7  0,1= 0,07; Р (
0,1= 0,07; Р (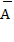 1А2) = Р (
1А2) = Р (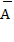 1)
1)  Р (А2) = 0,3
Р (А2) = 0,3  0,9 =...
0,9 =...
Тогда Р (А)= Р (А1 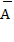 2)
2)  Р (
Р (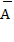 1А2) = 0,07
1А2) = 0,07  0,27 =...
0,27 =...
3. Событие B ={цель поражена хотя бы одним стрелком} означает, что либо цель поразил первый стрелок, либо цель поразил второй стрелок, либо цель поразили оба стрелка.
Событие 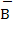 = {цель не поражена ни одним стрелком} является противоположным событию В, а значит Р(В) = 1
= {цель не поражена ни одним стрелком} является противоположным событию В, а значит Р(В) = 1  Р (
Р (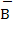 ).
).
Событие B̄ означает одновременное появление независимых событий 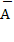 1 и
1 и 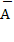 2, следовательно Р (
2, следовательно Р (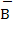 ) = Р (
) = Р (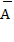 1
1 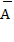 2) = Р (
2) = Р (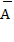 1)
1)  Р (
Р (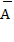 2) = 0,3
2) = 0,3  0,1 = 0,03. Тогда Р (В) = 1
0,1 = 0,03. Тогда Р (В) = 1  Р (
Р ( ) = 1
) = 1  0,03 =...
0,03 =...
Ответ: 1) 0,34; 2) 0,97.
Пример 6. Выпущено 1000 лотерейных билетов: на 5 из них выпадает выигрыш в сумме 500 рублей, на 10 – выигрыш в 100 рублей, на 20 – выигрыш в 50 рублей, на 50 – выигрыш в 10 рублей. Определить закон распределения вероятностей случайной величины X – выигрыша на один билет.
Решение: По условию задачи возможны следующие значения случайной величины X:
0, 10, 50, 100 и 500.
Число билетов без выигрыша равно 1000 – (5+10+20+50) = …, тогда P(X=0) = 915/1000 =...
Аналогично находим все другие вероятности: P(X=0) = 50/1000=…, P(X=50) = 20/1000=…,
P(X=100) = 10/1000=…, P(X=500) = 5/1000=... Полученный закон представим в виде таблицы:
| Значения xi | 0 | 10 | 50 | 100 | 500 |
| Вероятности pi | 0,915 | 0,05 | 0,02 | 0,01 | 0,005 |
Пример 7. a)Закон распределения случайной величины X имеет вид:
| X | –1 | 0 | 1 | 2 |
| P | 0,1 | 0,2 | 0,3 | 0,4 |
Вычислить Dx и Ϭx.
Решение: Найдем вначале математическое ожидание случайной величины X:
Mx = 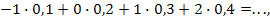 .
.
Вычислим дисперсию Dx:Dx =  .
.
Тогда среднее квадратическое отклонение: Ϭx =  .
.
Ответ: Dx = 1, Ϭx = 1.
б) Закон распределения случайной величины X имеет вид:
| X | 0 | 1 | 2 |
| P | 0,1 | 0,2 | x |
Найти x. Составить функцию распределения. Вычислить: P{X> 0,7}, Mx, Dx и Ϭx.
|
|
|
Решение. Согласно условию нормировки имеем уравнение: 0,1 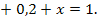 Отсюда x = 0,7. Далее, воспользовавшись рядом распределения, найдем:
Отсюда x = 0,7. Далее, воспользовавшись рядом распределения, найдем:
P{X> 0,7} = P {X = 1}  P{X = 2} = 0,2
P{X = 2} = 0,2 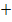 0,7 = …; Mx =
0,7 = …; Mx = 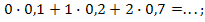
Dx = 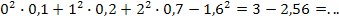 ; Ϭx =
; Ϭx =  .
.
Ответ: x = 0,7; P{X> 0,7} = 0, 9; Mx 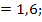 Dx
Dx 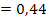 ; Ϭx
; Ϭx 
Пример 8. a)Известно, что случайная величина X, принимающая два значения x1 = 2 и x2 = 3, имеет математическое ожидание, равное 2,2. Построить ряд распределения случайной величины X, найти дисперсию, среднее квадратическое отклонение и составить функцию распределения.
Решение. Пусть P{X = 2} = p. Тогда, согласно условию нормировки,P{X = 3} = 1  . Используя определение математического ожидания, получим Mx = 2p
. Используя определение математического ожидания, получим Mx = 2p 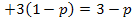 . Имеем уравнение 3
. Имеем уравнение 3 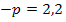 , откуда находим p = 0,8. Ряд распределения имеет вид:
, откуда находим p = 0,8. Ряд распределения имеет вид:
| X | 2 | 3 |
| P | 0,8 | 0,2 |
Теперь вычислим дисперсию и среднее квадратическое отклонение:
Dx =  ; Ϭx =
; Ϭx =  .
.
Согласно определению функция распределения имеет вид
Fx(x) = 
Ответ: Dx  ; Ϭx =
; Ϭx =  Fx(x) =
Fx(x) = 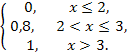
б) Возможные значения случайной величины X таковы: x1 = 2, x2 = 3, x3 = 3. Известно, что Mx = 2,3,α2 = 5,9. Найти вероятности, соответствующие возможным значениям X, и записать ряд распределения.
Решение. Ряд распределения, с учетом возможных значений случайной величины X, будет выглядеть следующим образом:
| X | 1 | 2 | 3 |
| P | p1 | p2 | p3 |
Найдем вероятности p1, p2 и p3, соответствующие возможным значениям X.
По условию Mx = 2,3, поэтому имеем первое уравнение, связывающее p1, p2 и p3:
 . Аналогично из условия α2 = 5,9 получим второе уравнение:
. Аналогично из условия α2 = 5,9 получим второе уравнение:
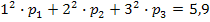 . Третье уравнение возникает из условия нормировки:
. Третье уравнение возникает из условия нормировки:
p1 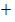 p2
p2 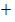 p3 = 1. Итак, имеем систему:
p3 = 1. Итак, имеем систему: 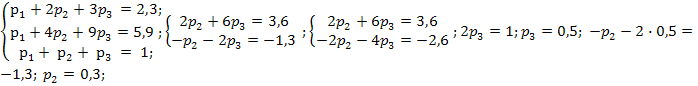

Ответ: ряд распределения имеет вид
| X | 1 | 2 | 3 |
| P | 0,2 | 0,3 | 0,5 |
2) Решить задачи (по примерам):
1) a)В партии из 100 деталей имеется 3 бракованных. Определить вероятность того, что, взятая наугад, деталь окажется стандартной.
б)Из 4 букв разрезной азбуки составлено слово «мама». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получится слово «мама».
2) a)В коробке лежат 5 зеленых, 3 синих и 12 красных карандашей. Вычислить вероятность того, что взятый наугад карандаш будет, синим или зеленым.
б) В урне лежат шары, двузначные номера которых составлены из цифр 1,2,3,4. Какова вероятность вынуть шар с номером 123?
3) a)Набирая номер телефона, абонент забыл последние 3 цифры и, помня лишь, что эти цифры различны, набрал их наугад. Найти вероятность того, что набраны нужные цифры.
б)Устройство содержит два независимо работающих элемента. Вероятности отказа элементов равны соответственно 0,04 и 0,09. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
|
|
|
4) a)Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9919. Найти вероятность попадания в цель при одном выстреле.
б)На полке в случайном порядке расставлено 21 книга, среди которых находится трехтомник Пушкина. Найти вероятность того, что эти тома стоят в порядке возрастания номера слева направо, но не обязательно рядом.
5) a)В коробке имеется 200 лампочек, из них 60 по 90Вт, 60 - по 60Вт, 40 - по 25Вт и 40 – по 15Вт. Определить вероятность того, что мощность любой наугад взятой лампочки не превысит 60Вт.
б) Вероятность поражения цели первым стрелком при одном выстреле равна 0,4, а вторым стрелком – 0,7. Найти вероятность того, что
1) цель будет поражена только одним стрелком;
2) цель будет поражена хотя бы одним стрелком.
Выпущено 200 лотерейных билетов: на 5 из них выпадает выигрыш в сумме 500 рублей, на 10 – выигрыш в 100 рублей, на 20 – выигрыш в 50 рублей, на 40 – выигрыш в 10 рублей. Определить закон распределения вероятностей случайной величины X – выигрыша на один билет.
7) a)Закон распределения случайной величины X имеет вид:
| X | –1 | 0 | 1 | 2 |
| P | 0,1 | 0,15 | 0,3 | 0,45 |
Вычислить Dx и Ϭx. б) Закон распределения случайной величины X имеет вид:
| X | 0 | 1 | 2 |
| P | 0,2 | 0,3 | x |
Найти x. Составить функцию распределения. Вычислить: P{X> 0,7}, Mx, Dx и Ϭx.
8) a)Известно, что случайная величина X, принимающая два значения x1 = 2 и x2 = 3, имеет математическое ожидание, равное 2,4. Построить ряд распределения случайной величины X, найти дисперсию, среднее квадратическое отклонение и составить функцию распределения.
б) Возможные значения случайной величины X таковы: x1 = 2, x2 = 3, x3 = 3. Известно, что Mx = 2,5,α2 = 6,7. Найти вероятности, соответствующие возможным значениям X, и записать ряд распределения.
Инструкционная карта
ПР № 7 «Вычисление числовых выражений».
Задание:
1) Перепишите и заполните пропуски:
Пример 1. Найдем значение выражения 800-625 + 331 +87– 119.
Решение: 800– 625 = …, 175 + 331 = …, 506 + 87 = …, 593 – 119 =...
Ответ: 474.
Пример 2. Найдем значение выражения 780: 39 • 212: 106 • 13.
Решение: Это выражение не содержит скобок, и в нем имеются действия только второй ступени, поэтому их следует выполнять по порядку слева направо:
780: 39 = …, 20 • 212 = …, 4240: 106 = …, 40 • 13 =...
Ответ: 520.
Пример 3. Найдем значение выражения 5781 –28 • 75: 25 + 156: 12.
Решение: Это выражение не содержит скобок, и в нем есть действия первой и второй ступени. Поэтому вначале выполним действия второй ступени:
28 • 75 = …, 2100: 25 = …, 156: 12 = …, а потом действия первой ступени:
5781 – 84 = …, 5697 + 13 =...
Ответ: 5710.
Пример 4. Найдем значение выражения 36 000: (62+ 14• 2) – 23 • 5.
Решение: Это выражение содержит скобки. Поэтому выполним сначала действия в скобках:
62 + 14 • 2 = 62 + 28 =... Подставив это значение, получим: 36 000: 90– 23 • 5 = 400 – 115 =...
Ответ: 285.
Пример 5. Запишите выражение по следующей программе вычислений:
1. Сложить числа 215 и 748.
2. Вычесть из 591 число 318.
3. Перемножить результаты команд 1 и 2.
Найдите значение этого выражения.
Решение: 1)215 + 748 = …,2)591 – 318 = …,3)963 × 273 = …
Ответ: 262899.
2) Решить задание (по примерам):
1. Найдите значение выражения:
а) 48 – 29 + 37 – 19;
б) 156 + 228 – 193 – 66;
в) 39 • 45: 65 • 2;
г) 1024: 128 • 15: 10;
д) 245: 7– 224: 16 + 35 • 11;
е) 322: 23 • 70 – 161 • 9: 69;
2. а) 315: (162 + 12 • 24 - 11 • 39) + 558: 31;
б) (24 • 7 - 377: 29) • (2378: 58 – 38);
в) (120 + 16 • 7) • 240: (300 – 5 • 44);
г) (372 + 118 • 6): (38 • 35 – 34 • 37) - 12;
д) 3124: (3 • 504 – 4 • 307) + 10 403: 101;
е) 15 + (12 322: (24 + 37) – 12 • 15): (35 • 2 – 59).
3. Измените порядок действий на основании свойств сложения, вычитания и умножения для удобства вычислений:
а) 348 + 54 + 46; г) 54 • 2 • 50;
б) 543 + 89 – 43; д) 34 • 8 + 66 • 8;
в) 427 – 33 – 67; е) 135 • 12 – 35 • 12.
|
|
|


