 |
Т Е С Т по теме «Перпендикулярность плоскостей».1 часть. 6 глава
|
|
|
|
3. Упростить:а) cos 2α  cos 6α – sin 2α
cos 6α – sin 2α  sin 6α;б) sin 3α
sin 6α;б) sin 3α  cos α
cos α  cos 3α
cos 3α  sin α;
sin α;
в) sin 2α  cos 3α
cos 3α 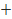 cos 2α
cos 2α  sin 3α; г)
sin 3α; г) 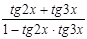 .
.
4. Упростить: а)cos α  cos β
cos β  sin α
sin α  sin β, еслиα = 42 °, β = 48 °;
sin β, еслиα = 42 °, β = 48 °;
б) cos(2 x – y)  cos(2 x + 3 y) + sin(2 x – y)
cos(2 x + 3 y) + sin(2 x – y)  sin(2 x + 3 y).
sin(2 x + 3 y).
5. Упростить выражение: 
6. Вычислите:cos450°– sin750°– сtg765°.
7. Вычислить 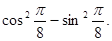
8. Вычислить 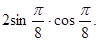
9. Вычислить sin2α, если sinα – cosα = 1/4.
10. Вычислить cos 2α, если sinα = – 0,8, 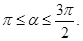
11. Вычислить sinα/2, cosα/2, tgα/2, ctgα/2, если sinα = 0,8, 
12. Пусть  Найдем sin2
Найдем sin2 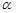 , cos2
, cos2 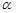 , tg2
, tg2 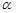 .
.
3) Решить задание:
1. Упростите выражение: sin(3 π/2 – α)· cos (π/2 + α) + sin(2 π – α) + cos (3 π/2 + α) + cosα ·sin α.
2. Найдите cos ß, если tgß = 7/24 и ß 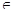 (π; 3 π/2).
(π; 3 π/2).
3. Найдите значение выражения: 2sin²2х – 9cos²2х, если cos2х = – 0,9.
4. Вычислите:3ctg60º· (sin310º cos 70º –sin70º cos 310º).
5. Найдите значение выражения:5 cos (3 π/2 + α), если α = 7π/6.
6. Найдите значение выражения: 4 + 5tg²х • cos²х, если sinх = 0,4.
7. Найдите значение выражения:7 cos (π + α) – sin(3 π/2 + α), если cosα = 0,6.
8. Упростить выражение 4⋅(tg(π – t) + ctg(π – t) + ctg(3π/2 – t))⋅ctg(π – t).
9. Упростите выражение: 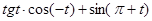 .
.
10. Вычислите: 
11. Докажите тождество: 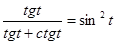 .
.
15. Упростите выражение: 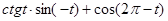 .
.
16. Вычислите 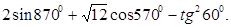
17. Найди значение выражения sin1050°+cos4620°+tg1035°.
18. Вычислите: 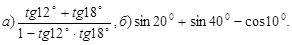
19. Упростите выражение 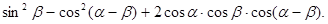
20. Вычислите: 
21. Упростите выражение: 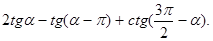
22. Вычислите: а) sin810° – cos900o+ tg585o – ctgl845o+ cosl35o – sin405°;
б) cosl05° – sinl95° + sin(-135°);
23. Найдите значение выражения sin (х + у), если sin х= 9/41; cos у = – 40/41; х - угол II четверти.
24. Найдите 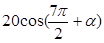 , если
, если 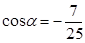 и
и 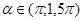 .
.
25. Найдите значение выражения 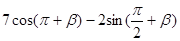 , если
, если 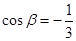 .
.
26. Упростить выражение: 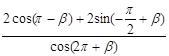 .
.
27. Упростите выражение:
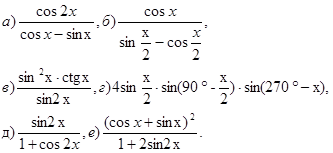
28. Вычислить 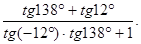
29. Дано: cos х =-12/13; 180 º < х < 270 º. Найти: cos х/2,tgx/2.
30. Упростите выражение 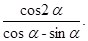
31. Упростите выражение 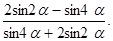
32. Найдите ctg 2α, если 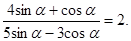
|
|
|
33. Найти значение выражения: 2sin150  cos150.
cos150.
34. Найти значение выражения: 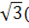 cos2150 – sin2150).
cos2150 – sin2150).
35. Вычислить: sin330º и ctg315º.
36. Упростите выражение:
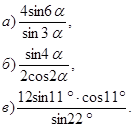
37. Найти значение выражения: 
38. Найдите значение выражения 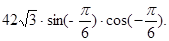
39. Найдите sin 2α,cos 2α,tg2α, если 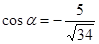 и
и 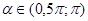 .
.
40. Найдите 24cos2α, если sinα = - 0,2.
41. Найдите tgα/2, если 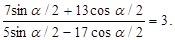 .
.
42. Найдите – 16cos2α, если sinα = – 0,6.
43. Найдите 22cos2α, если cosα = – 0,8.
44. Найдите 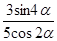 , если sin2α = 0,6.
, если sin2α = 0,6.
45. Найдите 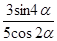 , если cos2α = 0,8.
, если cos2α = 0,8.
46. Упростите выражение 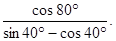
47. Упростите выражение: с tg² х · sin²х – cos 2 х.
48. Найдите sin 2 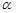 , если 3sin
, если 3sin 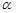 + 3cos
+ 3cos 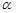 = 1.
= 1.
49. Найдите cos 2 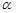 , если
, если 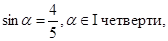
50. Вычислите без помощи таблиц:1) sin 75°; 2) cos 75°; 3)tg75°; 4) ctg 75°.
51. Вычислите без помощи таблиц и калькулятора: 1) sin 15°; 2) tg22,5°.
52. Упростите выражение:
Инструкционная карта
ПР № 10 «Решение простейших тригонометрических уравнений и неравенств».
Задание:
1) Перепишите и заполните пропуски:
Пример 1. Решите уравнение sin4x – cos2x = 0.
Решение: sin4x – cos2x = 0, 2sin2x cos2x – cos2 x = 0, сos2x(2sin2x – 1)=0,
сos2x=0 или sin2x=1/2.
2x = π/2 + π k, k 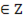 , 2x = (
, 2x = (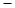 1) n
1) n  π/6 + π n, n
π/6 + π n, n  Z.
Z.
х1= π/…+ π k/2, k  Z, x2 = (
Z, x2 = ( 1)n
1)n 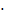 π/…+ π n/2, n
π/…+ π n/2, n  Z.
Z.
Ответ: х1= π/4+ π k/2, k 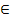 Z; x2 = (
Z; x2 = (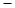 1)n
1)n 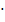 π/12+ π n/2, n
π/12+ π n/2, n 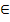 Z.
Z.
Пример 2. Решите уравнение (2 sinx – 1)  (tgx
(tgx  ) = 0.
) = 0.
Решение: (2 sinx – 1)  (tgx
(tgx  ) = 0,
) = 0,
2 sinx – 1= 0 или tgx  = 0,
= 0,
sinx = 1/2 tgx = 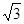 ,
,
х1= (–1) n 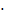 π/… + πn, n
π/… + πn, n  Z, х2 = π/… + πk, k
Z, х2 = π/… + πk, k 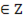 .
.
Ответ: х1= (–1) n 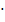 π/6 + πn, n
π/6 + πn, n 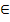 Z, х2 = π/3 + πk, k
Z, х2 = π/3 + πk, k 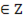 .
.
Пример 3. Решите уравнение (ctgx – 1)  (2sin
(2sin  + 1) = 0.
+ 1) = 0.
Решение: (ctgx – 1)  (2sin
(2sin  + 1) = 0,
+ 1) = 0,
ctgx – 1 = 0 или 2sin  + 1 = 0,
+ 1 = 0,
ctgx = 1 sin  = – 1/2, х/2 = (–1) n +1
= – 1/2, х/2 = (–1) n +1 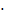 π/6 + πn, n
π/6 + πn, n 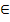 Z,
Z,
х1 = π/… + πk, k 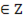 , х2 = (–1) n +1
, х2 = (–1) n +1 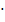 π/… + 2πn, n
π/… + 2πn, n 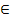 Z.
Z.
Ответ: х1 = π/4 + πk, k 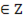 , х2 = (–1) n +1
, х2 = (–1) n +1 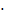 π/3 + 2πn, n
π/3 + 2πn, n 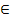 Z.
Z.
Пример 4. Решите уравнение 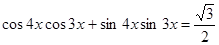 . Решение:
. Решение: 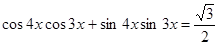 , cos (4x– 3x) =
, cos (4x– 3x) = 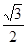 , cosx =
, cosx = 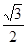 , x =
, x = 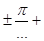 2πn, n∈Z. Ответ: x =
2πn, n∈Z. Ответ: x = 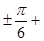 2πn, n∈Z.
2πn, n∈Z.
Пример 5. Решите уравнение 2cos(х + π/3) =  .
.
Решение: 2cos(х + π/3) =  , cos(х + π/3) = –
, cos(х + π/3) = – 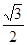 , х + π/3 = ± 5π/6+2πn, n∈Z, x = – π/3 ± 5π/6 + 2πn, n∈Z. x1 = – π/3 + 5π/6+2πn, n∈Z, x1 = π/… +2πn, n∈Z,
, х + π/3 = ± 5π/6+2πn, n∈Z, x = – π/3 ± 5π/6 + 2πn, n∈Z. x1 = – π/3 + 5π/6+2πn, n∈Z, x1 = π/… +2πn, n∈Z,
|
|
|
x2 = –π/3 – 5π/6+2πn, n∈Z, x2 = –7π/… +2πn, n∈Z.
Ответ: x1 = π/2 +2πn, n∈Z,x2 = –7π/6 +2πn, n∈Z.
Пример 6. Решите уравнение sin(2х + π/2) = 0.
Решение: sin(2х + π/2) = 0,2х + π/2 = πn, n∈Z,2х = – 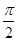 + πn, n∈Z,х = –
+ πn, n∈Z,х = – 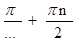 , n∈Z.
, n∈Z.
Ответ: х = = –  , n∈Z
, n∈Z
Пример 7. Решите уравнение a) arccos  б)arcsin (5x+2) = 0.
б)arcsin (5x+2) = 0.
Решение: a)arccos  cos(arccos
cos(arccos 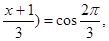
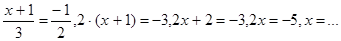 ,
,
б) sin(arcsin (5x+2)) = sin0, 5x + 2 = 0, 5x = – 2,x = …
Ответ: a) – 2,5, б) – 0,4.
Пример 8. Решите уравнение arctg (4x – 1) = 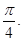
Решение: tg(arctg (4x – 1)) = tg  4x – 1 = 1, 4x = 2, x = … Ответ: 0,5.
4x – 1 = 1, 4x = 2, x = … Ответ: 0,5.
Пример 9. Решить неравенство sin(t) 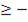 1/2.
1/2.
Решение: Рисуем единичную окружность. Так как sin(t) по определению - это координата y, отмечаем на оси Оу точку у = 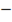 1/2. Проводим через неё прямую, параллельную оси Ох. В местах пересечения прямой с графиком единичной окружности отмечаем точки Pt1 и Pt2. Соединяем двум отрезками начало координат с точками Pt1 и Pt2.
1/2. Проводим через неё прямую, параллельную оси Ох. В местах пересечения прямой с графиком единичной окружности отмечаем точки Pt1 и Pt2. Соединяем двум отрезками начало координат с точками Pt1 и Pt2.
 Решением данного неравенства будут все точки единичной окружности расположенные выше данных точек. Другими словами решением будет являться дуга l. Теперь необходимо указать условия, при которых произвольная точка будет принадлежать дуге l.
Решением данного неравенства будут все точки единичной окружности расположенные выше данных точек. Другими словами решением будет являться дуга l. Теперь необходимо указать условия, при которых произвольная точка будет принадлежать дуге l.
Pt1 лежит в правой полуокружности, её ордината равна  1/2,
1/2,
тогда t1= arcsin( 1/2) =
1/2) =  π/6. Для описания точки Pt1 можно записать следующую формулу: t2 = π – arcsin(
π/6. Для описания точки Pt1 можно записать следующую формулу: t2 = π – arcsin( 1/2) = 7π/6. В итоге получаем
1/2) = 7π/6. В итоге получаем
для t следующее неравенство: 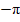 /6
/6 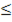 t
t 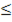 7π/6,Мы сохраняем знаки неравенств. А так как функция синус функция периодичная, значит решения будут повторяться через каждые 2π. Это условие добавляем к полученному неравенству для t и записываем ответ.
7π/6,Мы сохраняем знаки неравенств. А так как функция синус функция периодичная, значит решения будут повторяться через каждые 2π. Это условие добавляем к полученному неравенству для t и записываем ответ.
Ответ: 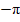 /6+2πn
/6+2πn 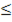 t
t 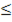 7π/6 + 2πn, при любом целом n.
7π/6 + 2πn, при любом целом n.
Пример 10. Решить неравенство cos(t) <1/2.
 Решение: Нарисуем единичную окружность. Так как согласно определению cos(t) это координата х, отмечаем на грфике на оси Ох точку x = 1/2.
Решение: Нарисуем единичную окружность. Так как согласно определению cos(t) это координата х, отмечаем на грфике на оси Ох точку x = 1/2.
Проводим через эту точку прямую, параллельную оси Оу. В местах пересечения прямой с графиком единичной окружности отмечаем точки Pt1 и Pt2. Соединяем двум отрезками начало координат с точками Pt1 и Pt2.
Решениями будут все точки единичной окружности, которые принадлежать
дуге l. Найдем точки t1 и t2. t1 = arccos(1/2) = π/3,
t2 = 2π  arccos(1/2) = 2π
arccos(1/2) = 2π 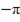 /3 = 5π/6.
/3 = 5π/6.
Получили неравенство для t: π/3 < t < 5π/6.
|
|
|
 Так как косинус - это функция периодичная, то решения будут повторяться через каждые 2π. Это условие добавляем к полученному неравенству для t и записываем ответ.
Так как косинус - это функция периодичная, то решения будут повторяться через каждые 2π. Это условие добавляем к полученному неравенству для t и записываем ответ.
Ответ: π/3+2πn <t<5π/6+2πn, для любого целого n.
Пример 11. Решить неравенство tg(t) 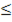 1.
1.
Решение: Период тангенса равняется π. Найдем решения, которые принадлежат промежутку (-π/2; π/2) правая полуокружность. Далее воспользовавшись периодичностью тангенса, запишем все решения данного неравенства. Нарисуем единичную окружность и отметим на ней линию тангенсов.
Если t будет являться решение неравенства, то ордината точки Т = tg(t) должна быть меньше или равна 1. Множество таких точек будет составлять луч АТ. Множество точек Pt, которые будут соответствовать точкам этого луча – дуга l. Причем, точка P(-π/2) не принадлежит этой дуге. Найдем условие, при котором некоторая точка Pt будет принадлежать дуге l. t1 = arctg(1) = π/4. Получаем неравенство 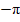 /2
/2 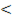 t
t  /4.
/4.
Учитывая период тангенса записываем ответ.
Ответ: 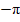 /2 + πn
/2 + πn 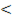 t
t  /4 + πn, для любого целого n.
/4 + πn, для любого целого n.
Пример 12. Решить неравенство: sin x > 0.
Решение: В пределах одного оборота единичного радиуса это неравенство справедливо
 при 0 < x <
при 0 < x <  . Теперь необходимо добавить период синуса 2
. Теперь необходимо добавить период синуса 2  n:
n:
 0 + 2πn
0 + 2πn 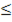 х
х 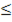 π + 2πn, 2πn
π + 2πn, 2πn 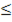 х
х 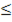 π + 2πn, при любом целом n.
π + 2πn, при любом целом n.
Ответ: 2πn 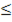 х
х 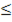 π+ 2πn, при любом целом n.
π+ 2πn, при любом целом n.
Пример 13. а) Решить неравенство: sin x > 0.5.
Решение: π/6 + 2πn < х < 5π/6 + 2πn, для любого целого n.
б) Решить неравенство cosх > 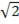 /2.
/2.
Решение: 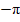 /4 + 2πn
/4 + 2πn 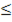 х
х 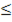 π/4 + 2πn, для любого целого n.(по рис.)
π/4 + 2πn, для любого целого n.(по рис.)
Пример 14. Решить неравенство cos (x/4 – 1) ≤  (
( /2).
/2).
Решение: Обозначим x/4 – 1 = у. Решая неравенство cos у ≤  (
(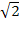 /2), находим
/2), находим
3π/4 + 2πn ≤ у ≤ 5π/4 + 2πn, n  Z.
Z.
Заменяя у = x/4 – 1, получаем 3π/4 + 2πn ≤ x/4 – 1 ≤ 5π/4 + 2πn, откуда
1 + 3π/4 + 2πn ≤ x/4 ≤ 1 + 5π/4 + 2πn, 4 + 3π + 8 πn ≤ х ≤ 4 + 5π + 8 πn, n  Z.
Z.
Ответ: 4 + 3π + 8 πn ≤ х ≤ 4 + 5π + 8 πn, n  Z.
Z.
2) Решить задание (по примерам):
1. Решите уравнение sin4x – cos2x = 0.
2. Решите уравнение (2 sinx 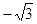 )
)  (tgx –
(tgx – 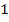 ) = 0.
) = 0.
3. Решите уравнение (ctgx 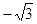 )
)  (2sin
(2sin  +
+ 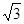 ) = 0.
) = 0.
|
|
|
4. Решите уравнениеcos 4x  cos3x + sin4x
cos3x + sin4x  sin3x =
sin3x = 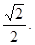
5. Решите уравнение 2cos(х + π/4) = – 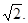
6. Решите уравнение sin(2х + π/3) = 0.
7. Решите уравнение a) arccos  б)arcsin (5x + 4) = 0.
б)arcsin (5x + 4) = 0.
8. Решите уравнение arctg (3x – 1) = 
9. Решить неравенство cos x ≤ - 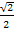 .
.
10. Решить неравенство sin x>- 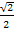 .
.
11. Решить неравенствоsin x ≥  .
.
12. Решить неравенство ctg x < -  .
.
13. Решить неравенствоtg x> 1.
14. Решить неравенство tg x ≤ 1.
15. Решить неравенство ctg x ≥ - 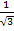 .
.
16. Решить неравенство сtg x ≤ 1.
3) Решить задание:
1. Решите уравнения:
|
|
|


