Т Е С Т по теме «Перпендикулярность плоскостей».1 часть. 2 глава

2) Обозначим верхнее основание трапеции - а, нижнее - b, высоту призмы h, тогда S(BB₁C₁C) = a h, 8 = a h, a = 8 / h, S(AA₁D₁D) = bh, 12 = bh, b = 12 / h, 

3) S₀ = (AD + BC) BH: 2 =(a + b)  BH: 2 = (8 / h + 12 / h)  5: 2 = … / h,

4)V= S₀ · h. V= 50 / h · h = … см³. Ответ: 50 см³.

Ø Д)Пример 1. В правильной четырехугольной пирамиде высота равна 9 см. Сторона основания 4 см. Найдите объем пирамиды.

Решение: V= 1/3 S₀ · h. V= 1/3 a ² · h = 1/3· 4²·9 = 1/3 · 16 · 9 = 16 · 3 = … см³. Ответ: 48см³.

Пример 2. a) Объем правильной четырехугольной пирамиды равен 27 см³, высота 9 см. Найти сторону основания.

Решение: V= 1/3 S₀ · h. V= 1/3 a ² · h, a ² = 3V: h = 3 · 27: 9 = 3 · 3 =..., a = …см.

Ответ: 3 см.

б) Объем пирамиды равен 56 см³, площадь основания 14 см². Чему равна высота?

Решение: V= 1/3 S₀ · h. h = 3 V: S₀ = 3 · 56: 14 = 3 · 4 = …  см.

Ответ: 12 см.

Пример 3. Дано: ABCD - правильная пирамида.

B

 АВ = a = 3; AD = 2  (рис.).Найти: a) Socн.; б) АО; в) DO; г) V.

Решение:

а) S₀ = 0,25  · a ² = 0,25 ·  3² = 2,25   (используем формулу для вычисления площади правильного треугольника).

б) AO = R = 2/3h = 1/3 a (формула радиуса описанной окружности через сторону правильного треугольника). AO = 1/3 · 3  =  .

в) DO² = AD² – AO², (по теореме Пифагора).

DO² = (2 )² – ()² = 4 · 3 – 3 = …, DO = h = 3.

г)V= 1/3 S₀ · h. V= 1/3 · 2,25  · 3 = … см³.

Ответ: a) Socн. = 2,25  см²; б) АО = см; в) DO = 3см; г) V = 2,25  см³.

Пример 4. Дано: ABCDF - правильная пирамида.

∠FCO = 45^°; FO = 2 (рис.). Найти: a) Socн.; б) V.

Решение:

1) Рассмотрим ΔFOC: ∠O = 90^°, ∠C = 45^°, значит, ∠F = 45^°. Следовательно, ΔFOC - равнобедренный, ОС ≈ FO = h= 2.

2) АС = 2OС = 4. d = AC = AD  (по свойству диагонали квадрата, d² = 2а²).

Тогда AD = AC /   = 4 /  = 2  .

3) ABCD - квадрат (пирамида правильная). S₀ = AD² = (2 )² = 2 · 4 =...

4) V= 1/3 S₀ · h. V= 1/3 · 8 · 2 = 16/3  5,3. 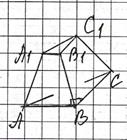Ответ: a) 8; 6) 5,3.

Пример 5. Дано: ABCA₁B₁C₁ – усеченная пирамида. ΔАВС  – прямоугольный,
AB = 18 дм, BC = 24 дм, AA₁ = BB₁ = СС₁ = 12,5 дм, k = 0,5. НайтиV.

Решение: S₁ = S_ABC = 1/2 · AB · BC = 1/2 · 18 · 24 = 9 · 24 = …,                       
S₂ = S(A₁B₁C₁)= 1/2· A₁B₁ · B₁C₁ = 1/2 (k · AB) · (k · BC) =                             
 = 1/2· 0,5 · 18 · 0,5 · 24 = 6 · 9 = …,
S = S₁ + S₂ +  = = 216 + 54 +  = 216 + 54 + 54   = …,          
V = 1/3 · h · S = 1/3 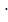 378 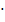 h = 126 h, R ₁ = a bc/4S₁, 

c =  =  = …,                                                                                              R₁ =  =  = …,

R₂ = R₁: 2 = 7,5; h² = 12,5² – (15 – 7,5)² = 12,5² – 7,5² = (12,5 – 7,5) · (12,5 + 7,5) =

= 5 · 20 = …, h = …,

V = 126 h = 126 · 10 = … (дм³).
Ответ: 1260 (дм³).

Пример 6. усеченная пирамида а) n = 3, а ₁ = 2, а ₂ = 5, h = 12, V =?                                                 
Решение: A = 2² + 5² + 2 · 5 = 39, V = · h · A = · 12 · 39 = …   .    Ответ: 39   .

б) n = 4, a ₁ = 3, a ₂ = 8, h = 6, V =?                                                                      
Решение: A = 3² + 8² + 3 · 8 = 97, V = 1/3 · 6 · 97 = 2 · 97 =...

Ответ: 194.

 

 

2) Решить задачи (по примерам):

А)

1. Высота правильной треугольной пирамиды 8 см, а ее апофемы 16см. Вычислите площадь боковой поверхности пирамиды.

2. Дано: усеченная правильная пирамида, n = 3, h = 8, a ₁= 14 , a ₂= 2  . Надо найти площадь полной поверхности усеченной пирамиды.

3. Дано: усеченная правильная пирамида, n = 4, h = 8, a ₁= 16, a ₂= 4. Надо найти площадь полной поверхности усеченной пирамиды.

4. Дано: усеченная правильная пирамида, n = 6, h = 2, a ₁= 4, a ₂= 8. Надо найти площадь полной поверхности усеченной пирамиды.

5. Дано: усеченная правильная пирамида, n = 4, h = 3, r₁=5, r₂= 9. Надо найти площадь полной поверхности усеченной пирамиды.

В)

1. Площадь грани прямоугольного параллелепипеда равна 15. Ребро, перпендикулярное этой грани, равно 6. Найдите объем параллелепипеда.

2. Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.

3. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3, 4. Диагональ параллелепипеда равна 13. Найдите объем параллелепипеда.

4. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3, 6. Объем параллелепипеда равен 108. Найдите его диагональ и высоту.

5. Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед, диагональ D₁B = 12 составляет угол в 30^° с плоскостью боковой грани, и угол в 45^° с боковым ребром. Найти: V.

6. Стороны основания прямоугольного параллелепипеда 6 и 8. Найти его объём, если высота равна длине диагонали его основания.

7. Найти объём прямоугольного параллелепипеда, если стороны основания 4 и 6, а диагональ параллелепипеда .

С)

1. Дано: АВСА₁В₁С₁ - прямая призма, АС = ВС, ∠ACB =90^°, BN = NA, ∠CNC₁ = 45^°, CC₁ = 8 (рис.). Найти: V.

2. Дано: ABCDА₁В₁С₁D₁ - прямая призма, ABCD - ромб, ∠BAD = 60^° (рис.). ВВ₁ = 4,               ∠B₁DB = 45^°. Найти: V.

3. Дано: ABCDFM...M₁ - правильная шестиугольная призма. AD₁ = 16 см - наибольшая диагональ.∠AD₁D = 30^° (рис.). Найти: V.

4. Дана трапеция, S(BB₁C₁C) = 10 см², S(AA₁D₁D) = 14см², BH = 10 см (рис.). Найти: Vnp.

Д)

1. В правильной четырехугольной пирамиде высота равна 6 см. Сторона основания 5 см. Найдите объем пирамиды.

2. a)Объем правильной четырехугольной пирамиды равен 48 см³, высота 4 см. Найти сторону основания. б) Объем пирамиды равен 28 см³, площадь основания 4 см². Чему равна высота?

3. Дано: ABCD - правильная пирамида. АВ = a = 6; AD = 4 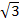 . Найти: a) Socн.; б) АО; в) DO; г) V.

4. Дано: ABCDF - правильная пирамида. ∠FCO = 45^°; FO = 4. Найти: a) Socн.; б) V.

5. Дано: ABCA₁B₁C₁ – усеченнаяпирамида. ΔАВС – прямоугольный,AB = 12 дм,BC = 16 дм, AA₁ = BB₁ = СС₁ = 13 дм, k = 0,5. Найти V.

6. а) n = 3, а ₁ = 2, а ₂ = 5, h = 24, V =?, б) n = 4, a ₁ = 3, a ₂ = 8, h = 3, V =?,

3) Решить задачи:

1. Дана правильная четырехугольная пирамида со стороной основания a=12 см и
высотой h=8 см. Найдите площадь полной поверхности пирамиды.

2. Найдите объем прямоугольного параллелепипеда с ребрами 3 см, 5 см и 8 см.

а) 120 см³; б) 60 см³; в) 32 см³; г) другой ответ.

3. Длина прямоугольной комнаты в 2 раза больше ширины и на 2 м больше высоты. Найдите объем комнаты, если ее длина равна 6 м. а) 432 м³; б) 144 м³; в) 72 м³; г) другой ответ.

4. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1; 0,5 и 16. Найдите ребро равновеликого ему куба.

Инструкционная карта

ПР № 4 «Вычисление координат векторов».

Задание:

1) Перепишите и заполните пропуски:
Пример 1. Дано:

Решение:

1) Находим координаты вектора

;

2) Затем находим координаты вектора

3) Теперь находим аналогично координаты вектора

4) Теперь находим сумму данных векторов, складывая соответствующие координаты:

Ответ:
Пример 2. Дано: , .Найдите

Решение: Первый случай

1) Находим координаты вектора

;

2) Затем находим разность векторов

;

3) Теперь находим длину вектора :

Второй случай

1) Находим координаты вектора

;

2) Находим координаты вектора

;

3) Затем находим сумму векторов

;

4) Теперь находим длину вектора : =

Ответ:

Пример 3. Даны векторы и 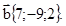. Найти

Решение: Для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем:

= 3  - 2 =  -  =
= = .

=   + 4 {7; -9;1 } =  + = =

=
Ответ: ,

Пример 4. Найдите сумму векторов:  и .

Решение: , .

Ответ:

Пример 5. Даны векторы , Найдите координаты векторов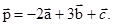

Решение: ,  , с ,

, .

Ответ: .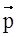

Пример 6. Дано: ΔАВС, А( 2; 0; 1), В( 1; 2; 3), С(8; 4; 9). ВМ - медиана.

Найти: координаты вектора .

Решение: По определению медианы, М - середина отрезка АС. Следовательно, координаты М найдем по формулам координат середины отрезка M ((8 2)/2, ( 4 + 0)/2,(9 + 1)/2), M(…,…,…). {3 + 1, 2 2,5 3},  {…,…,…}. Ответ: {4; 4; 2}.

Пример 7. Дано: А( 1; 5; 3), В(7; 1; 3), С(3; 2; 6). Доказать: ΔABC - прямоугольный.

Решение: По формуле расстояния между двумя точками найдем длины отрезков АВ, АС, ВС.
AB² = (7 + 1)² + (5 + 1)² + (3 – 3)², AB² = 64 + 36 = …, BC² = (7– 3)² + (– 2 + 1)² + (6 – 3)²,
BC² = 16 + 1 + 9 = …, AC² = (3 + 1)² + (5 + 2)² + (6 – 3)², AC² = 16 + 49 + 9 =...

Проверим равенство АВ² = ВС² + АС², 100 = 26 + 74 верно.

По теореме обратной теореме Пифагора делаем вывод, что ΔABC - прямоугольный
с гипотенузой АВ.

Пример 8. Дано: ΔАВС; М, N, К - середины сторон соответственно АВ, ВС, АС. М(3; 2; 5),
N(3,5; 1; 6), К( 1,5; 1; 2). Найти: координаты А, В, С.

Решение: Пусть A (х₁; у₁; z₁), В(х₂; у₂; z₂), С(х₃; у₃; z₃). По формулам координат середины отрезка составим системы для абсцисс, ординат и аппликат. Пользуясь методом сложения, решим эту систему:

1)

2)

3)

Ответ: А( 2; 0; 1), В(8; 4; 9), С( 1; 2; 3).

Пример 9. Дано: А(-2; 1; 2), B(-6; 3; -2), С ∈ оси OZ; АС = ВС. Найти: координаты точки С.

Решение: По условию С ∈ оси OZ, значит она имеет координаты С(0; 0; z) и АС = ВС. Составим уравнение, пользуясь формулой расстояния между двумя точками: 4 + 1 + (z 2)² = 36 + 9 + (z + 2)², 5 + z² – 4z + 4 = 45 + z² + 4z + 4, 8z = 40, z = …       Ответ: (0; 0; 5).

Пример 10. Дано: А( 2; 1; 2), B( 6; 3; 2), С (0; 0; 5); АС = ВС. Найти: S(ΔABC).

Решение: По формуле координат середины отрезка АВ найдем координаты точки М — середины:
M (( 6 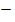2)/2, (1 + 3)/2,(2 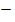2)/2), M( 4,2,0). AB² = ( 6 + 2)² + (3 1)² + (2 + 2)² = 16 + 4 + 16 = …, AB =... СМ-высота равнобедренного ΔABC.
CM² = ( 4 0)² + (2 0)² + (0  ( 5))² = 16 + 4 + 25 = …, CM = 3  ,
S(ΔABC) = AB· CM: 2 = 6 · 3  : 2 = … . Ответ: 9 .

2) Решить задачи (по примерам):

1. Дано:А(2;–1;6), В (2;0; –1), С(1; – 5; 0)

Предыдущая1234567891011121314Следующая

Поделиться:

Воспользуйтесь поиском по сайту: