Главная | Обратная связь | Поможем написать вашу работу!

Т Е С Т по теме «Перпендикулярность плоскостей».1 часть. 3 глава

2. Дано: , , 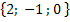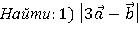; 2) .

3. Даны векторы и ,. Найти

4. Найдите сумму векторов: 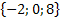и .

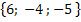5. Даны векторы 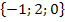, , . Найдите координаты векторов

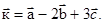
6. Дано: ΔАВС; А( 1; 2; 3), B(1; 0; 4), С(3; 2; 1). AM - медиана.Найти: координаты вектора

7. Дано: А( 1; 5; 3), В( 1; 3; 9), С(3; 2; 6).Доказать: ΔAВС - прямоугольный.

8. Дано: ΔАВС, М, N, К - середины сторон соответственно AB, BС, AС. М(3; 2; 4),
N( 6; 4; 10), К( 7; 2; 12).Найти: координаты вершин А, В, С.

9. Дано: A(4; 5; 4), B(2; 3; 4); С ∈ оси OX, AC = ВС. Найти: координаты точки С.

10. Дано: А(4; 5; 4), B(2; 3; 4), С(1; 0; 0), АС = ВС. Найти: S(ΔABC).

3) Решить задачи:

А)

1. Найдите координаты вектора , если

2. Даны векторы {–1;3; – 3} и . Найдите координаты и длину вектора .

3. Даны векторы {3;1; –2} и . Найдите координаты вектора ,

4. Найдите длину вектора , , 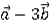если {2;1; –5} и .

5. Из точки А построен вектор . Найдите координаты точки В, если:

А(3;1; – 2), .

6. Даны точки А(4;6; –2) и В (–10;6; 0). Найти длину отрезка АВ.

7. Даны точки: А(10;14; 4), В (10;8; 12), С (18;8; 18)

Выяснить, равнобедренный ли треугольник, построенный на этих точках.

8. а) Даны два вектора: и 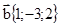.Найти .

б) Даны четыре вектора: .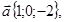

Найти координаты векторов

9. В кубе АВСDА₁В₁С₁D₁, сторона которого равна 3, на диагоналях граней АD₁ и D₁В₁ взяты точки Е и К так, что D₁Е: АD₁= 2: 3, D₁K: D₁B₁= 1: 3. Найдите длину отрезка DK.

10. Дано:

11. Найдите длину вектора КА ⊥АС, диагонали ромба 6 и 8 см.

12. Даны точки А(2;3; –1) иВ (–5;3; 0). Найти длину отрезка АВ.

13. Даны точки: А(5;7; 2), В (5;4; 6), С (9;4; 9) Выяснить, равнобедренный ли треугольник.

14. Даны два вектора: и .Найти .

В)

1. Дано: A (10, 4, –3), B (–6, 2, 1). Найти координаты точки M – середины отрезка AB.

2. Дано: A (5, 4, 7), B (10, 10, 0). Найти координаты вектора .

3. Дано: {0, 5, 0}, {2, –2, 1}. Найти длину векторов.

4. Даны точки А (1,5; 1; –2), B (2; 2; –3); и C (2; 0; –1). Найдите: периметр треугольника ABC.

5. Дано: М(–4; 7; 0) N(0; –1; 2).Найти: расстояние от начала координат до середины отрезка MN.

6. В кубе АВСDА₁В₁С₁D₁, сторона которого равна 3, на диагоналях граней АD₁ и D₁В₁
взяты точки Е и К так, что D₁Е: АD₁= 1: 3, D₁K: D₁B₁= 2: 3.

Найдите длину отрезка DK.

7. Даны четыре вектора: .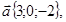

Найти координаты векторов

8. Дано:

9. Даны векторы и Найдите координаты вектора .

10. Даны векторы 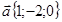, . Найдите координаты вектора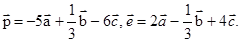

11. На каком расстоянии от плоскости (хОу) находится точка А(2; –3; –5).

12. На каком расстоянии от начала координат находится точка А(–3; 4; 0).

13. Найти длину вектора если А(5; 3; 2), В(3; –1; –4).

14. На каком расстоянии от плоскости (yOz) находится точка В(–3; 2; –4).

15. Даны векторы и . Найдите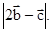

16. Изобразить систему координат Оху: и построить точку А(1; –2; –4).
Найти расстояние от этой точки до координатных плоскостей.

17. Вершины ΔАВС имеют координаты А(–2; 0; 1), В(–1; 2; 3), С(8; –4; 9).
Найдите координаты вектора если ВМ - медиана ΔABC.

18. Даны точки А(–1; 5; 3) В(7; –1; 3) С(3; –2; 6). Доказать, что ΔАВС - прямоугольный.

19. Даны точки А(–2; 1; 2), В(–6; 3; –2) на оси аппликат.
Найти точку С, равноудаленную от точек А и В.

20. Дано: А(2; 5; 8), В(6; 1;0).На оси ординат найти точку С, равноудаленную от точек А и В.
Найти: площадь ΔABC.

21. Даны точки А(–2; 1; 2), В(–6; 3;–2) на оси аппликат. Найти точку С, равноудаленную от
точек А и В. Найти площадь ΔАВС.

22. Середины сторон ΔАВС имеют координаты: М(3; –2; –4). N(–6; 4; –10), К(–7; 2; –12).
Найдите координаты вершин ΔАВС.

23. Даны точки А(4; 5; 4), В(2; 3; –4) на оси абсцисс. Найти точку С, равноудаленную от точек А и В. Найти площадь ΔABC.

24. Даны точки А(–3; 1; 2) и В(1; –1; –2). Найдите: а) координаты середины отрезка АВ;

б) координаты и длину вектора в) координаты точки С, если .

25. Даны точки А(0; 4; 0), В(2; 0; 0), С(4; 0; 4) и D(2; 4; 4). Докажите, что ABCD - ромб.

26. Даны точки А(0; 1; 2), В(√2; 1; 2), С(; 2; 1) и D(0; 2; 1). Докажите, что ABCD- квадрат.

27. Даны точки А(2; 1; –8), В(1;–5; 0), С(8; 1; –4). Докажите, что ΔАВС - равнобедренный и
найдите длину средней линии треугольника, соединяющей середины боковых сторон.

28. 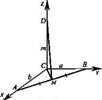Даны координаты трех вершин параллелограмма ABCD:
А(–6; –4; 0), В(6; –6; 2), С(10; 0; 4). Найдите координаты точки D и
угол между векторами и .

29. Дано: О(0; 0; 0), А(4; 0; 0), В(0; 6; 0), С(0; 0; –2).
ΔAОВ - вписанный в окружностьW(D; r).
Найти: а) координаты центра окружности D;
б) r- радиус окружности.

30. Дано: ΔАВС - прямоугольный; АС, ВС - катеты;AC = b = 9;BC = a = 12;
CD = m = 4; CD ⊥ (ABC); М - середина гипотенузы АВ. Найти: DM.

Инструкционная карта

ПР № 5 «Решение комбинаторных задач».

Задание:

1) Перепишите и заполните пропуски:

Пример 1. а)Сколько трехзначных чисел можно записать, используя цифры 1,3,6,7,9, если каждая их них может быть использована в записи только один раз?

Решение: по формуле получаем: способов.

Ответ: 60.

б)Из 20 учащихся надо выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать?

Решение: по формуле получаем: 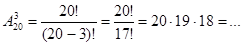способов.

Ответ: 6840.

в)Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?

Решение: Два юноши не могут одновременно пригласить одну и ту же девушку. И варианты,

при которых одни и те же девушки танцуют с разными юношами, считаются разными, поэтому:

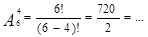
Ответ: 360.

Пример 2. а)Сколькими способами можно представлять друг с другом цифры 1, 2, 3, 4?

Решение: Р₄=4!= =…

Ответ: 24.

б)За столом пять мест. Сколькими способами можно расставить пятерых гостей?

Решение: Р₅=5!=

Ответ: 120.

в)Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?

Решение: На первое место можно поставить любой из четырех шариков (4 способа), на

второе – любой из трех оставшихся (3 способа), на третье место – любой из

оставшихся двух (2 способа), на четвертое место – оставшийся последний шар.

Всего 4 · 3 · 2 · 1 = 24 способа. Р₄ = 4! = 1 · 2 · 3 · 4 = 24. Ответ: 24 способа.

г)Сколькими способами можно переставить буквы слова «ананас»?

Решение: всего букв 6. Из них одинаковы n₁«а»=3, n₂«н»=2, n₃«с»=1. Следовательно, число различных перестановок равно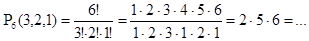

Ответ: 60.

Пример 3. а) Из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?

Решение: каждый выбор отличается от другого хотя бы одним дежурным. Значит, здесь речь идет о сочетаниях из 15 элементов по 3. Следовательно, по формуле получаем

Ответ: 455.

б)На полке стоит 12 книг: англо-русский словарь и 11 художественных произведений на английском языке. Сколькими способами читатель может выбрать 3 книги, если:

1) словарь нужен ему обязательно; 2) словарь ему не нужен?

Решение:

1) 2)

Ответ: 1)55,2) 165.

в) Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?

Решение: Выбор 6 из 10 без учёта порядка: способов.

Ответ: 210 способов.

г) Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр.

Решение:Так как кнопки нажимаются одновременно, то выбор этих трех кнопок – сочетание. Отсюда возможно вариантов.

Ответ: 120.

Пример 4. а)Сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи числа каждую из них не более одного раза?

Решение: для того, чтобы не пропустить и не повторить ни одно из чисел, будем записывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4, и, наконец, с цифры 7:14, 17, 41, 47, 71, 74.

Ответ: 6.

б) На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать?

Решение: Составим таблицу:

п люшка б утерброд пр яник к екс

кофе	КП	КБ	КПР	КК
сок	СП	СБ	СПР	СК
кефир	КЕП	КЕБ	КЕПР	КЕК

В ней три строки и четыре столбца, они образуют 12 клеток. Так как выбор еды и напитка происходит независимо, то в каждой клетке будет стоять один из возможных вариантов завтрака и, наоборот, любой вариант завтрака будет записан в одной из клеток. Значит, всего вариантов столько же, сколько клеток в таблице.

Ответ: 12.

Пример 5. а) Имеются 10 различных книг, три из которых – справочники. Сколькими способами

можно расставить эти книги на полке так, чтобы все справочники стояли рядом?

Решение: Т.к. в справочники должны стоять рядом, то будем рассматривать их как одну книгу. Тогда на полке надо расставить 10 – 3 + 1= … книг. Это можно сделать P₈ способами. Для каждой из полученных комбинаций можно сделать P₃ перестановок справочников.

Поэтому число способов расположения книг на полке равно произведению:

P₈· P₃= 8! · 3! = 40320 · 6 =...

Ответ: 241920.

б) Сколько всего существует результатов опыта, заключающегося в подбрасывании двух одинаковых игральных костей?

Решение: Формула числа сочетаний из m элементов по n элементов с повторениями имеет вид:

,
Ответ: 21.

2) Решить задание (по примерам):

1. а)Сколько трехзначных чисел можно записать, используя цифры 1,2,4,6,7,9, если каждая их них может быть использована в записи только один раз?

б)Из 15 учащихся надо выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать?

в)Сколькими способами четверо юношей могут пригласить четырех из пяти девушек на танец?

2. а)Сколькими способами можно представлять друг с другом цифры 1, 2, 3, 4,5?

б)За столом семь мест. Сколькими способами можно расставить семерых гостей?

в)Сколькими способами можно выложить в ряд красный, черный, синий, белый и зеленый шарики?

г)Сколькими способами можно переставить буквы слова «Миссисипи»?

3. а) Из 25 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?

б)На полке стоит 15 книг: англо-русский словарь и 14 художественных произведений на английском языке. Сколькими способами читатель может выбрать 3 книги, если:
1) словарь нужен ему обязательно; 2) словарь ему не нужен?

в) Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 7 книг?

г) Сколько четырехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр.

4. а)Сколько двузначных чисел можно составить из цифр 1,4,5,7, используя в записи числа каждую из них не более одного раза?

б) На завтрак Вова может выбрать бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать?

5. а)Имеются 10 различных книг, 6 из которых – справочники. Сколькими способами

можно расставить эти книги на полке так, чтобы все справочники стояли рядом?
б) Сколько всего существует результатов опыта, заключающегося в подбрасывании трех одинаковых игральных костей?

3) Решить задание:
подсчет числа размещений, перестановок, сочетаний.

1. «Вороне где-то Бог послал кусочек сыра», колбасы, хлеба и шоколада. «На ель Ворона взгромоздясь, позавтракать совсем уж было собралась, да призадумалась»: если есть кусочки по очереди, то из скольких вариантов придется выбирать?

2. Сколькими способами можно из 25 учащихся выбрать 5 для участия в школьном марафоне?

3. Сколькими способами могут быть распределены золотая и серебряная медали по итогам первенства по футболу, если число команд 12?

4. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?

5. Из 12 солдат нужно в разведку послать 5. Сколькими способами это можно сделать?

6. Сколько пятизначных чисел можно составить, используя только цифры 3 и 5?

7. «Проказница Мартышка, Осел, Козел и косолапый Мишка затеяли сыграть квартет». Сколькими способами они могут распределить четыре имеющихся у них инструмента?

8. «Проказница Мартышка, Осел, Козел и косолапый Мишка затеяли сыграть квартет». На складе 12 музыкальных инструментов. Мишке поручили принести со склада 8 любых инструментов. Сколько вариантов выбора есть у мишки?

9. Гера, Афина и Афродита попросили Париса не только назвать самую красивую из них, но и указать, кто «на втором и третьем местах». Сколько есть вариантов ответа?

10. В магазине «Филателия» продается 8 различных наборов марок, посвященных «Дню Победы». Сколькими способами можно сформировать из них 3 набора?

11. Сколько существует способов составить расписание уроков на один день из 6 предметов?

12. Алфавит племени тумба-юмба состоит из букв А, У, С. Словом является любая последовательность из 4 букв. Сколько слов в языке этого племени?

13. Сколькими способами можно выложить в ряд красный, зеленый, черный, синий кубики?

14. Из колоды в 36 карт вынимают 5 карт. Найдите число всех возможных вариантов выбора.

15. В классе 27 учеников, из которых нужно выбрать троих: первый ученик должен решить задачу, второй – сходить за мелом, третий – пойти дежурить в столовую. Сколькими способами это можно сделать?

16. Сколькими способами можно из 6 человек составить комиссию, состоящую из двух человек?

17. В соревновании участвуют 10 человек. Сколькими способами могут распределиться между ними места?

18. Сколькими способами можно расставить на полке 4 различные книги?

19. Сколько различных словарей необходимо переводчику, чтобы он мог переводить с любого из 5 языков – русского, английского, немецкого, французского, испанского – на любой другой из этих языков?

20. Пять человек обменялись друг с другом фотографиями. Сколько всего фотографий было?

21. На плоскости отмечены 6 точек. Каждые две точки соединили отрезком. Сколько получилось отрезков?

22. Сколькими способами можно переставить 5 различных геометрических фигур?

23. Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»?

24. За свои рисунки ученик получил две положительные оценки. Какими они могут быть? Сколько вариантов?

25. Сколько флагов можно составить из трех разных цветов, если имеются полосы синего, белого, красного цветов?

26. В понедельник в пятом классе 5 уроков. Сколькими способами можно составить расписание на понедельник?

27. Из десяти учащихся надо выбрать старосту, физорга и культорга. Сколькими способами это можно сделать?

28. В соревновании участвуют 10 человек. Сколькими способами могут распределиться между ними места?

29. У одного человека 7 книг по математике, а у второго – 9. Сколькими способами они могут обменять друг у друга две книги на две книги.

30. Имеется пять различных стульев и семь рулонов обивочной ткани различных цветов. Сколькими способами можно осуществить обивку стульев.

31. На памятные сувениры в «Поле Чудес» спонсоры предлагают кофеварки, утюги, телефонные аппараты, духи. Сколькими способами 9 участников игры могут получить эти сувениры? Сколькими способами могут быть выбраны 9 предметов для участников игры?

32. Сколькими способами можно расставить на шахматной доске 8 ладей так, чтобы на одна из них не могла бить другую?

33. Сколько может быть случая выбора 2 карандашей и 3 ручек из пяти различных карандашей и шести различных ручек?

34. На ферме есть 20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью? Если такой выбор уже сделан, сколькими способами можно сделать его еще раз?

35. Сколько существует четных пятизначных чисел, начинающихся нечетной цифрой?

36. В 9 классе учатся 7 учащихся, в 10 - 9 учащихся, а в 11 - 8 учащихся. Для работы на пришкольном участке надо выделить двух учащихся из 9 класса, трех – из 10, и одного – из 11. Сколько существует способов выбора учащихся для работы на пришкольном участке?

37. Сколько наборов из семи пирожных можно составить, если в продаже имеется четыре сорта пирожных?

перебором вариантов:

38. № 1. Запишите все двузначные числа, в записи которых используются только цифры 3, 5, 7, 9. Сколько двузначных чисел можно записать, если использовать при записи числа каждую цифру только один раз?

39. № 2. В четверг в первом классе должно быть три урока: русский язык, математика и физкультура. Сколько различных вариантов расписания можно составить на этот день?
Указание: Перебирая варианты введите обозначения:
Р – русский язык, М – математика, Ф – физкультура.

40. № 3. Саша выбрал в библиотеке 5 книг, но одновременно можно взять только две книги. Сколько вариантов выбора двух книг есть у Саши?

41. № 4. Школьники из Волгограда собрались на каникулы поехать в Москву, посетив по дороге Нижний Новгород. Сколькими различными способами могут ребята осуществить свое путешествие, если из Волгограда в Нижний Новгород можно отправиться на теплоходе ли поезде, а из Нижнего Новгорода в Москву – на самолете, теплоходе, поезде или автобусе?

42. № 5. Девять школьников, сдавая экзамены по математике и английскому языку, получили отметки «4» и «5». Можно ли утверждать, что по крайней мере двое из них получили по каждому предмету одинаковые отметки?

43. №6. Сколько существует двузначных чисел, у которых первая цифра больше второй?

44. №7. Несколько стран в качестве символа своего государства решили использовать флаг в виде четырех вертикальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг.
а) Сколько всего стран могут использовать такую символику?
б) Сколько всего стран могут использовать такую символику с верхней белой полосой?
в) Сколько всего стран могут использовать такую символику с нижней зеленой полосой?
г) Сколько всего стран могут использовать такую символику с синей и красной полосами, расположенными рядом?

Предыдущая 1 2 3 456 7 8 9 10 11 12 13 14 Следующая

Воспользуйтесь поиском по сайту: