 |
Внеаудиторная самостоятельная работа
|
|
|
|
| 1. Работа со справочным материалом: «Действия с дробями», «Признаки делимости», «Приближённые вычисления». |
2. Составить сообщение «Правила быстрого счёта»
3. Составить доклады: 1.«Формы комплексных чисел. Геометрический смысл»;
. «Значение комплексных чисел при решении уравнений»
Тема 2. Корни, степени и логарифмы
Устный опрос
1. Дайте определение корня n – ной степени.
2. Перечислите свойства корней.
3. Определение степени с рациональным показателем.
4. Дайте определение понятию функция.
5. Назовите известные вам функции, укажите их формулу и график.
6. Какими свойствами могут обладать функции?
7. Перечислите свойства показательной функции.
8. Перечислите свойства логарифмической функции.
Практическая работа 2.
Цель: проверить умение находить значение корня.
1. Вычислите значение выражения:
1)  ;
;
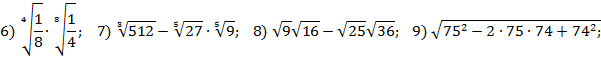

2. Упростите выражение:

Практическая работа 3.
Цель: проверить умение находить значение степени, выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней.
1. Вычислите значение выражения:


Практическая работа 4.
Цель: проверить умения находить значения логарифма на основе определения, выполнять преобразования выражений, применяя формулы, связанные со свойствами логарифмов.
1. Вычислите:


 .
.
2. Упростите выражение:


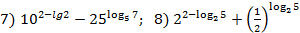 .
.
Практическая работа 5 (1 часть).
Цель: проверить умение решать показательные и логарифмические уравнения.
Вариант I
1.  2.
2. 
3.  4.
4. 
5. 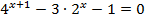 6.
6. 
7.  8.
8. 
9.  10.
10. 
|
|
|
Вариант II
1.  2.
2. 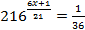
3.  4.
4. 
5. 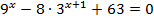 6.
6. 
7.  8.
8. 
9.  10.
10. 
Вариант III *
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 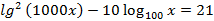
Практическая работа 5 (2 часть).
Цель: проверить умение решать показательные и логарифмические неравенства.
Вариант I
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 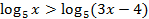
9.  10.
10. 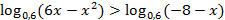
Вариант II
1.  2.
2. 
3. 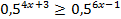 4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
Вариант III *
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
Самостоятельная работа 1.
| 1 вариант | 2 вариант | |
| 1. Вычислить: | ||
| а) | а)  ; б) ; б)  . .
| |
| в) | в)  г) г) 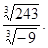
| |
| 2. Упростите выражение: | ||
а)  б) б) 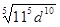 ;
в) ;
в)  . .
| а) в) | |
| 3*. Вынесите множитель из-под знака корня. | ||
 Самостоятельная работа 2.
Самостоятельная работа 2.
|
| |
| 1 вариант | 2 вариант | |||
| 1. Вычислите: | ||||

| 
| |||
| 2. Упростите: | ||||
| а) б) | а) б) | |||
| 3. Найдите значение выражения: | ||||

| 
| |||
| 4. Упростите выражение:
| ||||
 . .
| 
| |||
| 5. Упростите, применив формулы сокращенного умножения: | ||||
(m-n 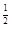 ) ) 
| 
| |||
Самостоятельная работа 3.
| № | Задание/ Ответы | 2 | 6 | 8 | ½ | -2 | 0 |
| 1 | log 525=х | ||||||
| 2 | log x36=2 | ||||||
| 3 | log 2x=3 | ||||||
| 4 | log 3  =x =x
| ||||||
| 5 | 
| ||||||
| 6 | 
| ||||||
| 7 | log5 1= x | ||||||
| 8 | lg100 = x | ||||||
| 9 | log10 0,01 = x | ||||||
| 10 | lg 
| ||||||
| 11 | lg 1 = x | ||||||
| 12 | 
|
Контрольная работа по теме «Корни, степени и логарифмы»
| 1 вариант | 2 вариант |
| 1. Вычислите: | |
 г)
г) 
|  г)
г) 
|
| 2. Решите уравнения: | |


| 

|
| 3. Решите неравенства: | |


| 

|
| 4*. Найдите корни уравнений: | |
 б)
б) 
| 

|
Внеаудиторная самостоятельная работа
1.Выполнение домашнего задания.
2.Составление тестовых заданий и эталон ответов по темам «Вычисление корней n-ой степени», «Степени с рациональным показателем».
3.Создать презентации по темам «История обозначения логарифмов», «Свойства логарифмов».
Тема 3. Прямые и плоскости в пространстве
Устный опрос
Способы задания плоскостей.
Взаимное расположение двух плоскостей.
Взаимное расположение прямой и плоскости.
Взаимное расположение двух прямых.
Признаки параллельности прямой и плоскости.
Признак параллельности плоскостей.
Определение перпендикулярных прямых.
Чему равен угол между двумя перпендикулярными прямыми.
Практическая работа 6
Цель: проверить умения распознавать на чертежах пространственные формы, описывать взаимное расположение прямых и плоскостей в пространстве, анализировать в простейших случаях взаимное расположение объектов в пространстве, использование при решении стереометрических задач планиметрические факты и методы.
1. Определи взаимное расположение данной прямой и плоскости.

Прямая DD1 и плоскость (XYZ)
Прямая LP и плоскость (AA1D)
Прямая XY и плоскость (CDD1)
Прямая DC и плоскость (AA1B)
Прямая MS и плоскость (ABC)
2. Точка C принадлежит отрезку AB. Через точку A проведена плоскость, через точки B и C проведены параллельные прямые, которые пересекают данную плоскость соответственно в точках B1 и C1.
|
|
|
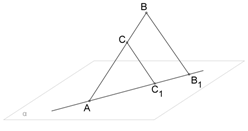
Вычисли длину отрезка CC1, если AC:BC=2:5 и BB1=9.
3. Точки M, N, P и Q являются соответственно серединами отрезков AD, CD, BC и AB.
Вычислите периметр четырёхугольника MNPQ, если AC= 13 см и BD= 14 см.

4. Точка O не находится в плоскости треугольника ABC. Точки D, E, F являются соответственно серединами отрезков AO, BO, CO.

Вычисли площадь треугольника DEF, если площадь треугольника ABC равна 136 см2.
5. Стороны ∡N пересекают параллельные плоскости α и β в точках A,B и C,D. Вычисли длину отрезка AB, если NA=13 см, NC=20 см и CD=57 см.

Практическая работа 7
Цель: проверить умения распознавать на чертежах пространственные формы, описывать взаимное расположение прямых и плоскостей в пространстве, анализировать в простейших случаях взаимное расположение объектов в пространстве, использование при решении стереометрических задач планиметрические факты и методы.
1. Проведенная к плоскости перпендикулярная прямая пересекает плоскость в точке O. На прямой отложен отрезок AD, точка O является серединной точкой этого отрезка. Определи вид и периметр треугольника ABD, если AD= 8 см, а OB= 4 см (ответ округли до одной десятой).

2. В тетраэдре DABC точка M делит пополам ребро DC. Дано, что у тетраэдра AD=ACBD=BC. Докажи, что прямая, на которой расположено ребро DC, перпендикулярна плоскости (ABM).
1. Определи вид треугольников.
ΔADC —
ΔDCB —
2. Какой угол образует медиана с основанием этих треугольников?

3. Прямая a пересекает плоскость β в точке C, и образует с плоскостью угол 30°. P∈a, точка R - проекция точки P на плоскость β. PC=10 см. Найди PR.
4. К плоскости α проведена наклонная, длина которой равна 50 см, проекция наклонной равна 30 см. На каком расстоянии от плоскости находится точка, из которой проведена наклонная?
5. Наклонная AD с плоскостью α образует угол 300, а наклонная DC с плоскостью α образует угол 450. Длина перпендикуляра DB равна 14 см. Вычисли длины обеих наклонных.

6. Длина отрезка VB равна 20 м. Он пересекает плоскость в точке O. Расстояние от концов отрезка до плоскости соответственно равны 8 м и 2 м. Найди острый угол, который образует отрезок VB с плоскостью.
|
|
|
7. Дан куб с некоторыми плоскостями сечений. Определи величины двугранных углов между плоскостями
1. (A1B1C1) и (ABC)
2. (ADD1) и (CDD1)
3. (ACC1) и (CDD1)

Тест 1.
1. Определи взаимное расположение данной прямой и плоскости.

1) Прямая AA1 и плоскость (CBB1)
2) Прямая BC и плоскость (A1B1C1)
3) Прямая CC1 и плоскость (ABA1)
4) Прямая CB1 и плоскость (BB1C1)
5) Прямая AB1 и плоскость (BCD)
2. Дан треугольник ABC. На сторонах AB и AC соответственно отложены точки D и E так, что DE=5 см и AD/BD=4/3. Через точки B и C проведена плоскость α, которая параллельна отрезку DE. Найти сторону ВС.

3. Точка O не находится в плоскости треугольника ABC. Точки D, E, F являются соответственно серединами отрезков AO, BO, CO.

Вычисли площадь треугольника DEF, если площадь треугольника ABC равна 236 см2.
4. Сторона AB правильного ABCDEF шестиугольника лежит в плоскости α.

Опиши взаимное расположение данных прямых и плоскости α, выбирая правильную характеристику из выпадающего списка.
Прямая DE ……α
Прямая FD ……α
Прямая EC……α
5. Стороны ∡M пересекают параллельные плоскости α и β в точках A, B и C, D. Вычисли длину отрезка AB, если MA=16 см, MC=20 см и CD=58 см.

6. Даны три параллельные плоскости α, β и γ. В каждой из них соответственно проведены прямые a, b и c.

Угол между прямыми a и b равен 340, угол между прямыми b и c равен 860. Определи угол между прямыми a и c.
7. Выбери правильный ответ из предложенных:
1. Как могут быть расположены две плоскости α и β, если…
1.1. одна из двух параллельных прямых находится в одной плоскости, а вторая прямая в другой плоскости (пересекающиеся, параллельны, параллельны или пересекаются)
1.2. у каждой прямой, которая находится в одной плоскости, можно найти параллельную прямую в другой плоскости
2. Как могут быть расположены две прямые, если они…
2.1. находятся каждая в одной из параллельных плоскостей (пересекающиеся или скрещивающиеся, параллельны или пересекаются, параллельны или скрещиваются)
2.2. находятся каждая в одной из пересекающихся плоскостей (параллельны или скрещивающиеся; параллельные, пересекающиеся или скрещивающиеся; пересекаются или скрещиваются).
|
|
|



 б)
б)  .
.  г)
г)  ;
; б)
б)  :
: 


 ;
;
 ;
;