 |
Контрольная работа по теме «Основы тригонометрии».
|
|
|
|
| ВАРИАНТ 1 | ВАРИАНТ 2 |
1°. Дано: cos a = –0,6, 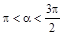 .
Вычислите: а) sin a; б) .
Вычислите: а) sin a; б)  .
2°. Решите уравнение:
а) 1 + sin x = 0;
б) 3cos x – 2sin2 x = 0.
3. Докажите тождество .
2°. Решите уравнение:
а) 1 + sin x = 0;
б) 3cos x – 2sin2 x = 0.
3. Докажите тождество
 .
4. Решите уравнение:
а) 1 + 3sin2 x = 2sin 2 x;
б) cos 4 x – cos 2 x = 0. .
4. Решите уравнение:
а) 1 + 3sin2 x = 2sin 2 x;
б) cos 4 x – cos 2 x = 0.
| 1°. Дано:  .
Вычислите: а) cos a; б) сtg (p – a).
2°. Решите уравнение:
а) cos x + 1 = 0;
б) 2cos2 x + 3sin x = 0.
3. Докажите тождество .
Вычислите: а) cos a; б) сtg (p – a).
2°. Решите уравнение:
а) cos x + 1 = 0;
б) 2cos2 x + 3sin x = 0.
3. Докажите тождество
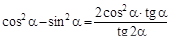 .
4. Решите уравнение:
а) 2sin x cos x = cos 2 x – 2sin2 x;
б) cos 4 x + cos 2 x = 0. .
4. Решите уравнение:
а) 2sin x cos x = cos 2 x – 2sin2 x;
б) cos 4 x + cos 2 x = 0.
|
| ВАРИАНТ 3 | ВАРИАНТ 4 |
1°. Дано: sin a = –0,6, 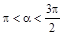 .
Вычислите: а) cos a; б) .
Вычислите: а) cos a; б)  .
2°. Решите уравнение:
а) 1 – sin x = 0;
б) 2cos2 x – cos x – 1 = 0.
3. Докажите тождество .
2°. Решите уравнение:
а) 1 – sin x = 0;
б) 2cos2 x – cos x – 1 = 0.
3. Докажите тождество
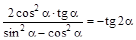 .
4. Решите уравнение:
а) .
4. Решите уравнение:
а) 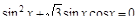 ;
б) sin 4 x – sin 2 x = 0. ;
б) sin 4 x – sin 2 x = 0.
| 1°. Дано:  Вычислите: а) sin a; б)
Вычислите: а) sin a; б) 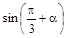 .
2°. Решите уравнение:
а) cos x = –1;
б) 2sin2 x – sin x – 1 = 0.
3. Докажите тождество .
2°. Решите уравнение:
а) cos x = –1;
б) 2sin2 x – sin x – 1 = 0.
3. Докажите тождество
 .
4. Решите уравнение:
а) .
4. Решите уравнение:
а) 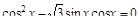 ;
б) sin 4 x + sin 2 x = 0. ;
б) sin 4 x + sin 2 x = 0.
|
| ВАРИАНТ 5 | ВАРИАНТ 6 |
1°. Дано: sin a = 0,8, 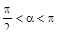 .
Вычислите: а) cos a; б) .
Вычислите: а) cos a; б)  .
2°. Решите уравнение:
а) .
2°. Решите уравнение:
а) 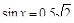 ;
б) 2sin2 x = cos x + 1.
3. Докажите тождество ;
б) 2sin2 x = cos x + 1.
3. Докажите тождество
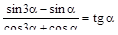 .
4. Решите уравнение:
а) sin2 x – 2sin x cos x = 3cos2 x;
б) sin 5x – sin x = 0. .
4. Решите уравнение:
а) sin2 x – 2sin x cos x = 3cos2 x;
б) sin 5x – sin x = 0.
| 1°. Дано: cos a = –0,6, 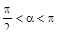 .
Вычислите: а) sin a; б) .
Вычислите: а) sin a; б)  .
2°. Решите уравнение:
а) .
2°. Решите уравнение:
а) 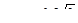 ;
б) 2cos2 x – 1 = sin x.
3. Докажите тождество ;
б) 2cos2 x – 1 = sin x.
3. Докажите тождество
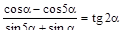 .
4. Решите уравнение:
а) sin2 x + sin x cos x = 2cos2 x;
б) sin 3x – sin x = 0. .
4. Решите уравнение:
а) sin2 x + sin x cos x = 2cos2 x;
б) sin 3x – sin x = 0.
|
| ВАРИАНТ 7 | ВАРИАНТ 8 |
1°. Дано:  .
Вычислите: а) sin a; б) sin 2a.
2°. Решите уравнение:
а) .
Вычислите: а) sin a; б) sin 2a.
2°. Решите уравнение:
а)  ;
б) sin2 x + 3cos x – 3 = 0.
3. Докажите тождество ;
б) sin2 x + 3cos x – 3 = 0.
3. Докажите тождество
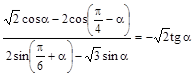 .
4. Решите уравнение:
а) sin2 x + sin x cos x = 2cos2 x;
б) cos x – cos 5x = 0. .
4. Решите уравнение:
а) sin2 x + sin x cos x = 2cos2 x;
б) cos x – cos 5x = 0.
| 1°. Дано:  .
Вычислите: а) cos a; б) cos 2a.
2°. Решите уравнение:
а) .
Вычислите: а) cos a; б) cos 2a.
2°. Решите уравнение:
а)  ;
б) 2cos2 x + sin x + 1 = 0.
3. Докажите тождество ;
б) 2cos2 x + sin x + 1 = 0.
3. Докажите тождество
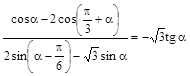 .
4. Решите уравнение:
а) 3sin2 x + sin x cos x = 2cos2 x;
б) cos 5x + cos x = 0. .
4. Решите уравнение:
а) 3sin2 x + sin x cos x = 2cos2 x;
б) cos 5x + cos x = 0.
|
Внеаудиторная самостоятельная работа
1.Выполнение домашнего задания.
2.Выполнить чертежи единичного круга. Указать на нём расположение табличных углов в градусах и радианах.
|
|
|
3.Выучить тригонометрическую таблицу.
4. Составить тестовые задания на тему «Тригонометрические формулы» и эталоны ответов.
5.Оформить справочник по математике по пройденному материалу.
6. Изучить таблицу Брадиса. Провести вычисления по таблице.
7.Работа со справочником.
8.Составить алгоритмы решения неравенств для функций у=tg(x) и у=ctg(x).
Тема 7. Функции и графики.
Устный опрос
Среди данных линий найти такую, которая является графиком какой-либо функции.
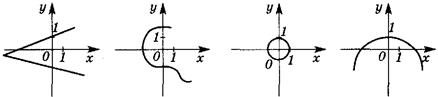
Среди данных таблиц найдите такую, которая является таблицей функции.
| х | 1 | 1 | 2 | х | 3 | 6 | 3 | х | 1 | 2 | 3 | ||
| у | 3 | 4 | 5 | у | 2 | 4 | 9 | у | 4 | 4 | 5 |
Среди формул а)  ; б)
; б) 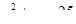 ; в)
; в)  найти такую, которая задает функцию.
найти такую, которая задает функцию.
Практическая работа 17. (4 часа)
Цель: проверить умение чтения графика, свойств графика, построение графика, схему исследования графика.
1. Проверить на четность и нечетность функции:
а) f (x)=(x 2 -1)3- x 4; б) f (x)= x 3 + x 5.
2. Определить область определения, область значений, промежутки монотонности функции, четность – нечетность, периодичность, экстремумы функции по графику:
а)
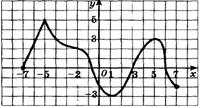
| б)
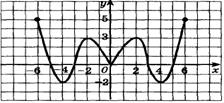
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в)
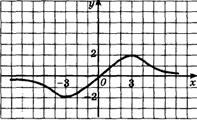
| г)

| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. Дана функция y = f (x). Вычислите ее значение при указанных значениях х. 1) 2) 3) 4) 4. Найдите область определения функции. 1) 7) 5. Найдите множество значений функции. 1) 6. По таблице значений переменных х и у определите вид зависимости между ними: а)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7. Дан график функции y= f(x). Определите по графику: а) область определения функции; б) множество значений функции; в) промежутки монотонности; г) нули функции; д) промежутки знакопостоянства; е) точки экстремума; ж) наибольшее и наименьшее значения; з) симметрию графика.
|
|
|
а) 
б) 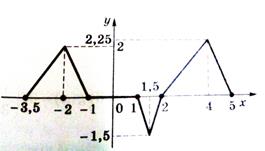
8. Постройте график зависимости:
а) y=-3 x; y=- x2; yx=2. б)  ;
;  ;
; 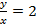 .
.
9. Известен вид зависимости и координаты точки Р, через которую проходит ее график. Напишите уравнение зависимости.
а) y = ax 2, P (2;8); б) 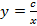 , P (2;
, P (2;  ).
).
10. Вычислите значение функции 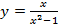 в точках 2 и 2t.
в точках 2 и 2t.
11. Найдите неизвестные координаты точек Р1(9; у1); Р2 (х1; 3), если эти точки принадлежат графику функции  .
.
12. Найдите область определения функции  .
.
13. Постойте график функции 
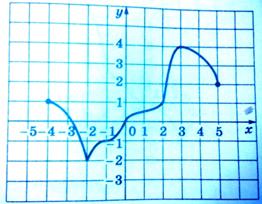
14. Дан график функции f. Определите по графику:
1) область определения функции;
2) множество значений;
3) промежутки монотонности;
4) точки экстремума;
5) какие значения функция принимает ровно один раз.

|
|
|



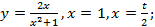

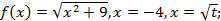
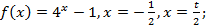
 2)
2)  ; 3)
; 3)  ; 4)
; 4) 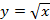 ; 5)
; 5) 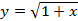 ; 6)
; 6) 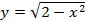 ;
; ; 8)
; 8)  .
.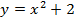 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 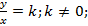 б) xy = c, c ≠0; в) у=ах2, а ≠ 0; г) у=ах+ b, b ≠0; д) ни одна из указанных.
б) xy = c, c ≠0; в) у=ах2, а ≠ 0; г) у=ах+ b, b ≠0; д) ни одна из указанных.