 |
Контрольная работа по теме «Координаты и векторы»
|
|
|
|
1 вариант.
DABC – тетраэдр, точка К – середина АС, точка М – середина KD,  . Разложите вектор
. Разложите вектор  по векторам
по векторам  .
.
Даны векторы  Найдите координаты вектора
Найдите координаты вектора  .
.
Дан треугольник MNC, вершины которого имеют координаты: M(2;-3;3), N(-1;1;-2) и C(5;3;1). Докажите, что треугольник равнобедренный и вычислите его площадь.
Найдите скалярное произведение 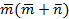 , если
, если  .
.
Даны точки С(3:-2:1), D(-1;2;1), M(2;1;3), N(-1;4;-2). Определите, будут ли прямые CM и DN перпендикулярны. Найдите длину вектора  .
.
2 вариант.
DABC – тетраэдр, точка К – середина АС, точка N – середина KD,  . Разложите вектор
. Разложите вектор  по векторам
по векторам  .
.
Даны векторы  Найдите координаты вектора
Найдите координаты вектора  .
.
Дан треугольник MNC, вершины которого имеют координаты: M(1;-4;2), N(-2;0;-3) и C(4;2;0). Докажите, что треугольник равнобедренный и вычислите его площадь.
Найдите скалярное произведение 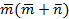 , если
, если 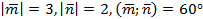 .
.
Даны точки С(3:-2:1), D(-1;2;1), M(4;2;6), N(-1;4;-2). Определите, будут ли прямые CM и DN перпендикулярны. Найдите длину вектора 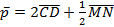 .
.
Внеаудиторная самостоятельная работа
| 1.Выполнение домашнего задания. 2.Выполнить чертежи различных пространственных единичных фигур с введёнными координатными осями. |
3.Определить координаты вершин выполненных фигур в заданной системе координат.
4. Подготовить презентацию на тему «Использование векторов при вычислении углов и расстояний в пространстве»
Тема 6. Основы тригонометрии.
Устный опрос
1. Переведите углы из градусной меры в радианную:
1) 36°; 3) –120°; 5) 870°; 7) –2510°;
2) 265°; 4) –135°; 6) 1020°; 8) –2940°.
2. Чему равна градусная мера углов:
1); 3); 5) – ; 7);
2); 4); 6) – ; 8)?
3. Найдите на числовой окружности точку, которая соответствует заданному числу:
|
|
|
1);; – ; 3);; –2p;
2) p;; – ; 4) 2p;; – .
Практическая работа 12.
Цель: закрепить умения вычисления значений тригонометрических функций, с использованием таблицы значений.
1. Вычислите:
1) 2sin 30° – tg 45° + ctg 30°;
2)  ;
;
3) 6cos 30° – 3tg 60° + 2sin 45°;
4)  ;
;
5) 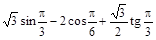 ;
;
6)  ;
;
7) 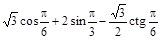 ;
;
8)  ;
;
9) 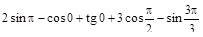 ;
;
10) 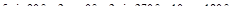 .
.
2. Найдите значение выражения:
1)  ;
;
2) 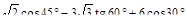 ;
;
3)  ;
;
4)  ;
;
6) 4cos 180° – 3sin 270° + 3sin 360° – ctg 90°.
Практическая работа 13.
Цель: проверить умения применять основные тригонометрические тождества для нахождения значений тригонометрических функций.
1. Определить, в какой четверти находится конечная точка поворота на угол a и каковы знаки cos a и sin a, если угол равен:
1) 260°; 3) 565°; 5) –915°; 7) 8760°;
2) 290°; 4) 480°; 6) –825°; 8) 8000°.
2. Определить знак каждого из данных произведений:
1) sin 100° × sin 132°; 5) ctg 300° × sin 222°;
2) cos 210° × sin 115°; 6) sin 118° × cos 118° × tg 118°;
3) cos 285° × cos 316°; 7) sin 2,1 × ctg 2,1 × cos 2,1;
4) tg 112° × sin 165°; 8) cos 123° × tg 123° × sin 312°.
3. Какой знак имеет произведение sin j × cos j × tg j, если число j равно:
1) 4,1; 2) – 240°; 3)?
4. Зная значение одной функции угла a, найдите значения остальных тригонометрических функций этого угла:
1)  ; 2)
; 2) 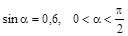 .
.
5.Вычислите остальные три тригонометрические функции, если:
1)  ; 2)
; 2)  .
.
Практическая работа 14. (4 часа)
Цель: проверить умение применять основные тригонометрические тождества для преобразования тригонометрических выражений.
1. Упростите выражения:
1) 4cos23a + 4sin23a; 2) 2sin25a + 2cos25a;
3) 1 – sin23 x; 4) 1 – cos24b;
5) sin27 y – 1; 6) cos23 t – 1;
7) 2sin2 t – 1; 8) 1 – 2cos23g;
|
|
|
9) tg 3b ctg 3b; 10) ctg 1,1 × tg 1,1;
11) tg a cos a; 12) sin 2j ctg 2j;
13) ctg2j sin2j; 14) tg2a cos2a;
15) tg g cos g sin g; 16) sin 2a cos 2a ctg 2a;
17) (1 – cos 3b)(1 + cos 3b); 18) (1 – sin 2j)(1 + sin 2j);
19) (sin t + 1) (sin t – 1); 20) (cos 5a – 1)(1 + cos 5a);
21) sin2g cos2g + cos4g; 22) sin4j + sin2j cos2j;
23) (sin a – cos a)2 + (sin a + cos a)2;
24) (3sin t + 4 cos t)2 + (4sin t – 3 cos t)2.
2. Преобразуйте следующие выражения:
1) sin2a + cos2a – cos2b; 13) cos2a + cos2a ctg2a;
2) tg x ctg x – cos23a; 14) sin4a + cos2a – cos4a;
3) tg25b + tg t ctg t; 15) sin4b + sin2b cos2b + cos2b;
4) (1 – sin23a) tg23a; 16) tg2j – sin2j – tg2j sin2j;
5) ctg2b(cos2b – 1) + 1; 17) (ctg2a – cos2a) tg2a;
6) 1 + cos2g – sin2g; 18) ctg2 y (1 – cos y)(1 + cos y);
7) 1 – sin a cos a ctg a; 19)  ;
;
8) (tg b cos b)2 + (ctg b sin b)2; 20)  ;
;
9) 2 – cos2j tg2j – cos2j; 21) 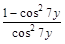 ;
;
10)  ; 22)
; 22)  ;
;
11)  ; 23)
; 23)  ;
;
12)  ; 24)
; 24)  .
.
3.Упростите выражения:
1) sin2 x – tg 2a ctg 2a; 10) sin2a tg2a + sin2a;
2) sin24a + tg2j + cos24a; 11) cos4 x – sin4 x + sin2 x;
3) tg 3 ctg 3 + ctg2 x; 12) sin2a + sin2a cos2a + cos4a;
4) 7 – 4sin2b – 4cos2b; 13) cos2 t + ctg2 t cos2 t – ctg2 t;
5) cos j ctg j sin j – 1; 14) (ctg2a – cos2a) tg2a;
6)  ; 15)
; 15)  ;
;
7)  ; 16)
; 16)  ;
;
8) 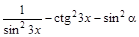 ; 17)
; 17)  ;
;
9) 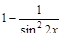 ; 18)
; 18)  .
.
4. Преобразуйте выражения:
1) 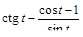 ; 7)
; 7)  ;
;
2) 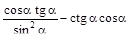 ; 8)
; 8)  ;
;
3)  ; 9) sin t cos t (tg t + ctg t);
; 9) sin t cos t (tg t + ctg t);
4)  ; 10) sin t – cos t (tg t + ctg t);
; 10) sin t – cos t (tg t + ctg t);
5)  ; 11)
; 11)  ;
;
6)  ; 12)
; 12)  .
.
5. Преобразуйте выражения:
1)  ; 6)
; 6)  ;
;
2) 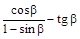 ; 7)
; 7)  ;
;
3) 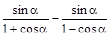 ; 8)
; 8) 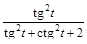 ;
;
4)  ; 9)
; 9)  .
.
5)  ;
;
Практическая работа 15.
Цель: проверить умения решать простейшие тригонометрические уравнения.
Вариант 1
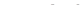


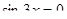

| Вариант




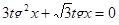
| Вариант 3
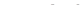




|
Вариант 4





| Вариант 5



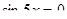

| Вариант 6





|
Вариант 7


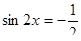


| Вариант 8


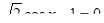

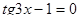
| Вариант 9





|
|
|
|


