 |
Практическая работа 18. (4 часа)
|
|
|
|
Цель: проверить умение построения графиков функций с помощью элементарных преобразований.
| 1 Вариант | 2 вариант |
1. Дана функция y = x 2. Постройте графики функций:
а) y = x2 – 3;
б) y = 2x2;
в) y = -2x2 + 3;
г) y = 2(x – 1)2 + 3.
2. Дана функция  . Постройте графики функций:
а) . Постройте графики функций:
а)  ;
б) ;
б)  ;
в) ;
в) 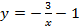 ;
г) ;
г)  ;
д) ;
д)  .
3. Дана функция .
3. Дана функция  . Постройте графики функций:
а) . Постройте графики функций:
а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г)  . .
| 1. Дана функция y = x 2. Постройте графики функций:
а) y = x2 + 2;
б) y = -2x2;
в) y = 3(x+2)2;
г) y = -(x – 3)2 - 2.
2. Дана функция  . Постройте графики функций:
а) . Постройте графики функций:
а)  ;
б) ;
б)  в)
в)  ;
г) ;
г)  ;
д) ;
д)  .
3. Дана функция .
3. Дана функция  . Постройте графики функций:
а) . Постройте графики функций:
а)  ;
б) ;
б)  ;
в) ;
в) 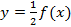 ;
г) ;
г)  . .
|
Самостоятельная работа 7.
| Вариант 1 | Вариант 2 |
| Вычислите значение функции | |

| 
|
| в точках | |
| Найдите неизвестные координаты точки | |
| M(9; y) | K(16; y) |
| если эта точка принадлежит графику функции | |
| По данному графику функции | |
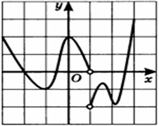
| 
|
| Определите знаки коэффициентов k и l, если график функции | |
| I, II, III четвертях | I, II, IV четвертях, |
| Известен вид зависимости и координаты точки P, через которую проходит её график. Напишите уравнение зависимости, если | |
 , P(2; 8) , P(2; 8)
| 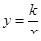 , , 
|
Тест 3.

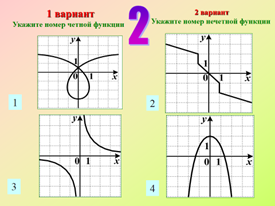



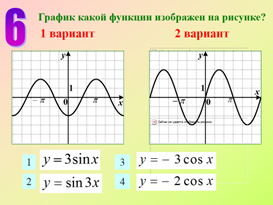


Контрольная работа по теме «Функции и графики»
| 1 вариант | 2 вариант |
| 1. По графику функции y = f (x) укажите: а) область определения функции; б) область значений; в) нули функции; г) промежутки знакопостоянства; д) точки максимума и минимума функции; е) промежутки монотонности; ж) наибольшее и наименьшее значения функции. | |
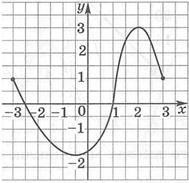
| 
|
| 2. В одной системе координат постройте графики функций: | |
y = cos x
y = cos  y = 2 cos x
y = 2 cos x
| y = sin x y =3 sin x y = sinx + 2 |
| 3*. Постройте график функции: | |

| 
|
Внеаудиторная самостоятельная работа
1.Выполнение домашнего задания.
|
|
|
2.Начертить графики сложных функций. Провести их исследование.
3. Создать презентацию на тему: «Использование периодических функций в физике и электротехнике».
4. Создать презентацию «Схема исследования функций и построение эскиза графиков».
5. Построить графики по всем видам преобразований.
Тема 8. Многогранники и круглые тела.
Практическая работа 19.
Цель: проверить умение находить элементы призмы.
1. Дано:
правильная четырехугольная призма.
Что является основанием данного тела? Совпадает ли высота с боковым ребром?
Ответ:
Основанием является...
Параллелограмм
Прямоугольник
Квадрат
Любой четырехугольник
Высота с боковым ребром...
не совпадает
совпадает
2. Сколько граней у пятиугольной призмы? (7)
3. Ребро куба равно 3 м. Вычисли угол, который образует диагональ куба с плоскостью основания.
Выбери правильный ответ:
60 градусов
45 градусов
arctg√2/2
arccos√3/3
30 градусов
4. Вычисли диагональ прямоугольного параллелепипеда, если его длина равна 18 см, ширина — 6 см и высота — 1 см. (19)
5. Стороны основания прямоугольного параллелепипеда равны 6 дм и 8 дм. Боковое ребро равно6 дм. Вычисли площадь диагонального сечения. (60)
6. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Углом между диагональю B1D прямоугольного параллелепипеда и боковой гранью DD1C1C является угол:

∢B1DC
∠B1DD1
∢B1DC1
∠B1DB
7. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 15 см и 20 см. Площадь большей боковой грани равна 75 см2. Вычисли высоту призмы. (3)
8. Основанием прямой призмы ABCKLN является равнобедренный треугольник.
Площадь грани AKLB равна 38√3 см2, угол ACB=120°, AC=CB=4 см. Вычисли площадь основания и высоту призмы. (4 l3)

Практическая работа 20.
Цель: проверить умение находить площадь поверхности и объем призм.
1.Объем комнаты 75м3, высота комнаты 3 метра. Найдите площадь пола.
|
|
|
2. Если каждое ребро куба увеличить на 2 см, то его объѐм увеличится на 98см3. Чему равно ребро куба?
3. Кирпич размером 25 * 12 * 6,5 см имеет массу 3,51 кг. Найти его плотность.
4.Чугунная труба имеет квадратное сечение, еѐ внешняя ширина 25 см, толщина стенок 3 см. Какова масса одного погонного метра трубы? (плотность чугуна 7,3 г/см3).
5. Бак, имеющий форму прямоугольного параллелепипеда с основанием 3,2м 1,2м, вмещает 9000 ц воды. Сколько квадратных метров оцинкованного железа пошло на его изготовление, если при этом на швы идѐт 5% материала?
6. Площадь поверхности куба равна 18. Найдите его диагональ.
7. Объём куба равен 8. Найдите площадь его поверхности.
8. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
9. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины. равны 2 и 6. Объём параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящие из той же вершины.
10. Основанием прямой треугольной призмы служит прямоугольной треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь её поверхности.
Практическая работа 21.
Цель: проверить умение находить элементы пирамид.
1. Сторона основания правильной четырехугольной пирамиды равна а, высота h. Найдите боковое ребро и апофему.
2. Основанием пирамиды служит ромб со стороной 13 см. Высота пирамиды проходит через точку пересечения диагоналей ромба и равна и12 см. Найдите боковые ребра пирамиды, если одна из диагоналей основания равна 10 см.
3. Основание пирамиды – прямоугольный треугольник с катетами 6 см и 8 см. Все двугранные углы при основании пирамиды равны 60. Найдите высоту пирамиды.
4. В правильной четырехугольной пирамиде сторона основания равна 8, а длина бокового ребра равна 9. Найдите высоту пирамиды.
5. В правильной треугольной пирамиде сторона основания равна 6, а длина бокового ребра равна 4. Найдите высоту пирамиды.
6. В правильной шестиугольной пирамиде сторона основания равна 4, а длина бокового ребра равна 8,5. Найдите высоту пирамиды.
7. Высота правильной четырехугольной пирамиды равна 10, а сторона основания равна 15. Найдите длину апофемы этой пирамиды.
8. Высота правильной треугольной пирамиды равна 2, а сторона основания равна 12. Найдите длину апофемы этой пирамиды.
|
|
|
9. Высота правильной шестиугольной пирамиды равна 4, сторона основания равна 2  . Найдите длину апофемы этой пирамиды.
. Найдите длину апофемы этой пирамиды.
Практическая работа 22.
Цель: проверить умения находить площади поверхностей и объем пирамид.
Вариант 1.
№1. В правильной треугольной пирамиде высота основания равна h, боковые ребра наклонены к основанию под углом 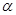 . Найдите объем пирамиды.
. Найдите объем пирамиды.
№2. Основанием пирамиды МАВСD служит ромб со стороной а и острым углом А, равным 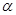 . Боковое ребро МВ перпендикулярно к плоскости основания, а грани МАD и МDС наклонены к нему под углом
. Боковое ребро МВ перпендикулярно к плоскости основания, а грани МАD и МDС наклонены к нему под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
№3. Стороны оснований правильной четырехугольной усеченной пирамиды равны  см и
см и  см. Площадь диагонального сечения равна 90 см2. Найдите объем пирамиды.
см. Площадь диагонального сечения равна 90 см2. Найдите объем пирамиды.
Вариант 2.
№1. В правильной четырехугольной пирамиде диагональ основания равна d. Боковые грани наклонены к основанию под углом 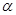 . Найдите объем пирамиды.
. Найдите объем пирамиды.
№2. Основанием пирамиды DАВС служит равнобедренный треугольник АВС. АВ=ВС= а,  . Ребро ВD перпендикулярно к плоскости основания, а грань АDС составляет с ним угол
. Ребро ВD перпендикулярно к плоскости основания, а грань АDС составляет с ним угол  . Найдите объем пирамиды.
. Найдите объем пирамиды.
№3. Стороны оснований правильной треугольной усеченной пирамиды равны 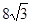 см и
см и  см. Площадь сечения, проходящего через боковое ребро пирамиды и середину противоположной стороны основания равно 54 см2. Найдите объем пирамиды.
см. Площадь сечения, проходящего через боковое ребро пирамиды и середину противоположной стороны основания равно 54 см2. Найдите объем пирамиды.
Вариант 3.
№1. Высота правильной четырехугольной пирамиды равна h, а плоский угол при вершине 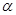 . Найдите объем пирамиды.
. Найдите объем пирамиды.
№2. В основании пирамиды лежит треугольник со сторонами 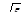 ,
, 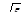 и 4. Боковые ребра наклонены к основанию под углом 450. Найдите объем пирамиды.
и 4. Боковые ребра наклонены к основанию под углом 450. Найдите объем пирамиды.
№3. В правильной треугольной усеченной пирамиде стороны основания равны a и b  . Боковое ребро равно
. Боковое ребро равно  . Найдите объем пирамиды.
. Найдите объем пирамиды.
Вариант 4.
№1. Высота правильной треугольной пирамиды равна h, а плоский угол при вершине пирамиды – 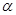 . Найдите объем пирамиды.
. Найдите объем пирамиды.
|
|
|
№2. В основании пирамиды лежит равнобедренная трапеция с углом 300.Боковые грани наклонены к основанию под углом 600. Высота пирамиды равна  . Найдите объем пирамиды.
. Найдите объем пирамиды.
№3. В правильной четырехугольной усеченной пирамиде стороны оснований равны т и 2 т, апофема пирамиды равна  . Найдите объем пирамиды.
. Найдите объем пирамиды.
Практическая работа 23.
Цель: проверить умение вычислять элементы, площади поверхностей и объемы цилиндра и конуса.
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
Объём первого цилиндра равен 12  . У второго цилиндра высота в три раза больше, а радиус основания - в два раза меньше, чем у первого. Найдите объём второго цилиндра. Ответ дайте в кубических метрах.
. У второго цилиндра высота в три раза больше, а радиус основания - в два раза меньше, чем у первого. Найдите объём второго цилиндра. Ответ дайте в кубических метрах.
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, делённую на 
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
Боковая поверхность конуса равна S б, а его радиус r. Найти высоту конуса, если: S б = 16p, r =3.
Образующая конуса а см, составляет с плоскостью основания угол b °. Определить объем конуса, если: а = 4, b = 30°.
Образующая конуса равна 30 см, образует с плоскостью основания угол 300. Найти высоту конуса.
Диаметр конуса равен 4 см, высота 6 см. Найти образующую конуса и боковую поверхность.
Практическая работа 24.
Цель: проверить умение находить объем шара и площадь сферы.
1. Поверхность шара равна  см2. Определить диаметр шара.
см2. Определить диаметр шара.
2. Поверхность шара равна  см2. Найти его радиус.
см2. Найти его радиус.
3. Сфера  проходит через вершины квадрата ABCD, сторона которого равна 12 см. Найдите расстояние от центра сферы – точки О до плоскости квадрата, если радиус OD образует с плоскостью квадрата угол, равный 60
проходит через вершины квадрата ABCD, сторона которого равна 12 см. Найдите расстояние от центра сферы – точки О до плоскости квадрата, если радиус OD образует с плоскостью квадрата угол, равный 60  .
.
4. Стороны треугольника АВС касаются шара. Найдите радиус шара, если АВ = 8 см, ВС= 10 см, АС = 12 см и расстояние от центра шара О до плоскости треугольника АВС равно  см.
см.
5. Сфера  проходит через вершины квадрата CDEF, сторона которого равна 18 см. Найдите расстояние от центра сферы – точки О до плоскости квадрата, если радиус сферы OЕ образует с плоскостью квадрата угол, равный 30
проходит через вершины квадрата CDEF, сторона которого равна 18 см. Найдите расстояние от центра сферы – точки О до плоскости квадрата, если радиус сферы OЕ образует с плоскостью квадрата угол, равный 30  .
.
6. Стороны треугольника MKN касаются шара. Найдите радиус шара, если MK = 9 см, MN= 13 см, KN = 14 см и расстояние от центра шара О до плоскости MKN равно  см.
см.
7. Куб, диагональ которого равна 4  см, описан около шара. Объём этого шара равен…
см, описан около шара. Объём этого шара равен…
|
|
|
Тест 4.
| Вариант 1. |
Назовите элемент, не принадлежащий цилиндру:
а) апофема; б) высота; в) образующая; г) радиус.
Осевым сечением цилиндра является:
а) треугольник; б) круг; в) прямоугольник; г) трапеция.
Полная поверхность цилиндра определяется по формуле, где R – радиус основания, L – образующая, Н – высота:
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  .
Выявите формулу, не относящуюся к вычислению поверхности или объема конуса, где L – образующая, R – радиус, Н – высота:
а) .
Выявите формулу, не относящуюся к вычислению поверхности или объема конуса, где L – образующая, R – радиус, Н – высота:
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  .
Площадь поверхности сферы определяется по формуле, где R – радиус сферы:
а) .
Площадь поверхности сферы определяется по формуле, где R – радиус сферы:
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
|
Какой не может быть призма?
а) прямой; б) наклонной; в) правильной; г) усеченной.
Прямоугольный параллелепипед – это:
а) пирамида; б) призма; в) октаэдр; г) тетраэдр.
Объем конуса определяется по формуле:
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  .
Апофема - это:
а) образующая б) высота в) высота боковой г) высота усечен-
цилиндра; конуса; грани пирамиды; ого конуса.
Если высота конуса равна 15, а радиус основания 8, то образующая конуса равна:
а) 14; б) 17; в) 13; г) 6.
Кирпич 2´3´6. Его диагональ равна:
а) 10; б) 6; в) 7; г) 5.
Радиус основания цилиндра равен 2 м, высота 3 м. Диагональ осевого сечения равна:
а) 5 м; б) 7 м; в) 8 м; г) 4 м. .
Апофема - это:
а) образующая б) высота в) высота боковой г) высота усечен-
цилиндра; конуса; грани пирамиды; ого конуса.
Если высота конуса равна 15, а радиус основания 8, то образующая конуса равна:
а) 14; б) 17; в) 13; г) 6.
Кирпич 2´3´6. Его диагональ равна:
а) 10; б) 6; в) 7; г) 5.
Радиус основания цилиндра равен 2 м, высота 3 м. Диагональ осевого сечения равна:
а) 5 м; б) 7 м; в) 8 м; г) 4 м.
|
Диаметр шара равен 2 см. Его объем и поверхность равны:
а)  см3 и 4p см2; б) см3 и 4p см2; б)  см2 и 4p см3; в) 4p2 см3 и p м; г) 2p см3 и p см2. см2 и 4p см3; в) 4p2 см3 и p м; г) 2p см3 и p см2.
|
| II вариант |
Цилиндром называется тело, ограниченное поверхностью:
а) конической; б) концентрической; в) цилиндрической; г) сферической.
Боковая поверхность цилиндра определяется по формуле, где R – радиус, L – образующая, Н – высота:
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  .
Конус не может быть получен вращением:
а) прямоугольника вокруг одной из сторон;
б) равностороннего треугольника вокруг медианы;
в) прямоугольного треугольника вокруг одного из катетов.
Назовите элемент, не принадлежащий конусу:
а) образующая; б) ось; в) высота; г) медиана.
Боковая поверхность усеченного конуса является:
а) частью цилиндрической поверхности;
б) частью конической поверхности;
в) частью сферической поверхности:
г) частью поверхности шара.
Сфера является поверхностью:
а) конуса; б) усеченного конуса; в) цилиндра; г) шара. .
Конус не может быть получен вращением:
а) прямоугольника вокруг одной из сторон;
б) равностороннего треугольника вокруг медианы;
в) прямоугольного треугольника вокруг одного из катетов.
Назовите элемент, не принадлежащий конусу:
а) образующая; б) ось; в) высота; г) медиана.
Боковая поверхность усеченного конуса является:
а) частью цилиндрической поверхности;
б) частью конической поверхности;
в) частью сферической поверхности:
г) частью поверхности шара.
Сфера является поверхностью:
а) конуса; б) усеченного конуса; в) цилиндра; г) шара.
|
Какая формула используется как для вычисления объема призмы, так и цилиндра, где R – радиус основания, Н – высота:
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  .
Назовите, какая фигура не является правильным многогранником:
а) куб; б) додекаэдр; в) октаэдр; г) параллелепипед.
Объем пирадмиды определяется по формуле, где S осн – площадь основания, Н – высота, R – радиус сферы:
а) .
Назовите, какая фигура не является правильным многогранником:
а) куб; б) додекаэдр; в) октаэдр; г) параллелепипед.
Объем пирадмиды определяется по формуле, где S осн – площадь основания, Н – высота, R – радиус сферы:
а) 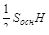 ; б) ; б)  ; в) ; в)  ; г) ; г)  .
Объем правильной треугольной пирамиды, высота которой равна 12 см, а сторона 13 см, равняется:
а) 156 см3; б) 207 см3; в) .
Объем правильной треугольной пирамиды, высота которой равна 12 см, а сторона 13 см, равняется:
а) 156 см3; б) 207 см3; в)  см3; г) см3; г)  см3.
Радиус основания цилиндра равен 2 м, высота 3 м. Диагональ осевого сечения равна:
а) 5 м; б) 7 м; в) 8 м; г) 4 м.
В основании прямого параллелепипеда лежит:
а) квадрат; б) параллелограмм; в) ромб; г) прямоугольник.
Диаметр шара равен 2 см. Его объем и поверхность равны:
а) см3.
Радиус основания цилиндра равен 2 м, высота 3 м. Диагональ осевого сечения равна:
а) 5 м; б) 7 м; в) 8 м; г) 4 м.
В основании прямого параллелепипеда лежит:
а) квадрат; б) параллелограмм; в) ромб; г) прямоугольник.
Диаметр шара равен 2 см. Его объем и поверхность равны:
а) 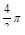 см3 и 4p см2; б) см3 и 4p см2; б) 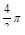 см2 и 4p см3; в) 4p2 см3 и p м; г) 2p см3 и p см2. см2 и 4p см3; в) 4p2 см3 и p м; г) 2p см3 и p см2.
|
|
|
|



 ,
, 

 найдите множество значений функции
найдите множество значений функции расположен в
расположен в