 |
Контрольная работа по теме «Интеграл и его применение».
|
|
|
|
Вариант 1.
1. Докажите, что функция 𝐹 является первообразной для функции 𝑓 на множестве 𝑅:
а) 𝐹 (𝓍) = 𝓍 4 – 3, 𝑓 (𝓍) = 4 𝓍 3 ;
б) 𝐹 (𝓍) = 
, 𝑓 (𝓍) = 
2. Вычислите интеграл:
а) 
;
б) 
3. Найдите общий вид первообразной для функции: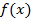 
= 𝐶𝑜𝑠2 𝓍 - 𝑆𝑖𝑛 2 𝓍.
4. Вычислите площадь фигуры, ограниченной линиями: 𝑦 = 2 – 𝓍 2 , 𝑦 = 0, 𝓍 = - 1, 𝑥 = 0.
Вариант 2.
1. Докажите, что функция 𝐹 является первообразной для функции 𝑓 на множестве 𝑅:
а) 𝐹 (𝓍) = 4𝓍 – 𝑥 3, 𝑓 (𝓍) = 4 – 3 𝓍2 ;
б) 𝐹 (𝓍) = 
, 𝑓 (𝓍) = 
.
2. Вычислите интеграл:
а) 
б) 
3. Найдите общий вид первообразной для функции: 
= 4 𝑆𝑖𝑛 𝓍 𝐶𝑜𝑠 𝓍.
4. Вычислите площадь фигуры, ограниченной линиями: 𝑦 = 4 – 𝓍2, 𝑦 = 0.
Внеаудиторная самостоятельная работа.
1.Выполнение домашнего задания.
2.Составить сообщение на тему: «История возникновения и обозначение интеграла».
3.Создать презентацию на тему: «Применение интегралов для вычисления площадей и объёмов нестандартных геометрических фигур»
Тема 11. Элементы теории вероятностей и математической статистики.
Устный опрос.
1. Что называется перестановкой элементов? По какой формуле вычисляется число перестановок?
2. Что называется размещением? По какой формуле вычисляется число размещений?
3. Что называется сочетанием? По каким формулам вычисляется число сочетаний?
4. Перечислите свойства сочетаний.
5. Что называют опытом или испытанием?
6. Что называют событием, случайным, достоверным и невозможным событиями?
7. Какие события называют совместными и несовместными?
|
|
|
8. Какие события называют противоположными?
9. Что называют полной группой событий?
10. Напишите формулу полной вероятности.
Практическая работа 33.
Цель: проверить умение находить вероятности событий.
1. В урне находиться 7 красных и 6 синих шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара красные (событие А)?
2. Девять различных книг расставлены наудачу на одной полке. Найти вероятность того, что четыре определенные книги окажутся поставленными рядом (событие С).
3. Из 10 билетов выигрышными являются 2. Определить вероятность того, что среди взятых наудачу 5 билетов, один выигрышный.
4. Из колоды карт (52 карты) наудачу извлекают 3 карты. Найти вероятность того, что это тройка, семерка, туз.
5. Ребенок играет с пятью буквами разрезной азбуки А, К, Р, Ш, Ы. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «Крыша».
6. В ящике находятся 6 белых и 4 красных шара. Наудачу берут два шара. Какова вероятность того, что они окажутся одного цвета?
7. В первой урне находятся 6 черных и 4 белых шара, во второй – 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми?
Практическая работа 34.
Цель: проверить умение применять вероятностные методы к решению практических задач.
1.Во время учебных маневров два танка пытаются прорваться в расположение противотанковой батареи «противника». Какова вероятность того, что будет подбит хотя бы один танк, если вероятность того, что будет подбит один танк, равна 2/3, а два танка – 2/5?
2. Электронный прибор состоит из двух последовательно включённых блоков. Вероятность выхода из строя за 1 месяц работы первого блока равна 1/3, второго – ¼, а обоих – 1/16. Найдите вероятность безаварийной работы прибора в течение месяца.
3. Вероятность рождения двух близнецов - мальчиков равна 0,33, а вероятность рождения мальчика равна 0,51. Найдите вероятность того, что второй из близнецов мальчик, при условии, что первый из них мальчик.
|
|
|
4. Было установлено, что при ремонте автомобильных двигателей деталь№1 заменялась в 45 % случаев, деталь №2 – в 40 % случаев, а обе эти детали – в 35 % случаев. Найти вероятность того, что при ремонте двигателя деталь №2 буде заменена при условии, что и деталь №1 заменена.
5. Вероятность того, что письмо находится в письменном столе, равна 4/5, причём с равной вероятностью оно может быть в любом, из восьми ящиков. Некто просмотрел 7 ящиков и письма не нашёл. Какова вероятность того, что письмо в восьмом ящике?
6. В ящике находится 12 деталей, из которых 8 стандартных. Рабочий берет наудачу одну за другой две детали. Найти вероятность того, что обе детали окажутся стандартными.
7. Рабочий обслуживает два автомата, работающих независимо друг от друга. Вероятность того, что в течение часа первый автомат не потребует внимания рабочего, равна 0,8, а для второго автомата эта вероятность равна 0,7. Найдите вероятность того, что в течение часа ни один и автоматов не потребует внимания рабочего.
8. В ящике в случайном порядке положены 10 деталей, из которых 4 стандартных. Контролер взял наудачу 3 детали. Найдите вероятность того, что хотя бы одна из взятых деталей окажется стандартной.
9. В ящике в случайном порядке положены 15 деталей, из которых 6 стандартных. Контролер по одной взял 4 детали. Найдите вероятность того, что все детали стандартные.
10. В ящике 15 красных и 5 синих пуговиц. Вынимаются наудачу 3 пуговицы. Какова вероятность, что пуговицы будут одноцветными?
|
|
|
