 |
Контрольная работа по теме «Многогранники и круглые тела».
|
|
|
|
Вариант 1.
1. Найдите боковое ребро правильной четырехугольной пирамиды, у которой сторона основания 8 м, а высота 10 м.
2. Основание прямой призмы АВСА1В1С1- прямоугольный треугольник с катетом 5 см и гипотенузой 13 см. Высота призмы 10 см. Найдите объем призмы.
3. Сторона основания правильной четырехугольной пирамиды равна 8 см, боковое ребро наклонено к плоскости основания под углом 45°. Найдите объем пирамиды.
4. Радиус основания цилиндра равен 5 см, а высота цилиндра равна 6 см. Найдите площадь сечения, проведённого параллельно оси цилиндра на расстоянии 4 см от неё.
5. Радиус шара равен 17 см. Найдите площадь сечения шара, удалённого от его центра на 15 см.
6. Радиус основания конуса равен 3 м, а высота – 4 м. Найдите образующую и площадь осевого сечения конуса.
Вариант 2.
1. В основании прямой треугольной призмы лежит прямоугольный треугольник с катетами 8 см и 6 см. Найдите боковое ребро призмы, если её боковая поверхность 120 см2.
2. Основание пирамиды – прямоугольник со сторонами 6 см и 8 см. Высота пирамиды равна 12 см и проходит через точку пересечения диагоналей основания. Найдите боковое ребро пирамиды.
3. В правильной четырехугольной пирамиде боковые грани наклонены к плоскости основания под углом 30°, а ребро основания равно 6 см. Найдите объем пирамиды.
4.Высота цилиндра – 8 дм, радиус основания – 5 дм. Цилиндр пересечён плоскостью параллельно оси так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси цилиндра.
5. Радиус сферы равен 15 см. Найдите длину окружности сечения, удалённого от центра сферы на 12 см.
6. Образующая конуса l наклонена к плоскости основания под углом в 30°. Найдите высоту конуса и площадь осевого сечения.
|
|
|
Внеаудиторная самостоятельная работа
1.Выполнение домашнего задания.
2.Выполнить макеты многогранников, описать их характеристики.
3. Создать презентацию «Геометрические тела вращения».
4.Работа со справочником.
5.Составление и решение задач прикладного и практического содержания.
Тема 9. Начала математического анализа»
Устный опрос
Сформулировать правила дифференцирования и записать производные основных элементарных функций:
| 1о. | 
| 8о. | 
|
| 2о. |
В частности, | 9о. | 
|
| 10о. | 
| ||
| 11о. | 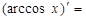
| ||
| 12о. | 
| ||
| 13о. | 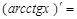
| ||
| 14о. | 
| ||
| 3о. | 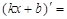
| 15о. | 
|
| 4о. |
В частности, | 16о. | 
|
| 17о. | 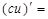
| ||
| 5о. |  В частности,
В частности, 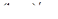

| 18о. |  В частности,
В частности, 
|
| 6о. | 
| ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ | |
| 7о. | 
| 19о. | 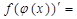
|
Практическая работа 25.
Цель: проверить умения вычислять производные элементарных функций.
| I вариант | II вариант |
| 1. Вычислить производную: | |
1)  ;
2) ;
2)  ;
3) ;
3)  ;
4) ;
4)  ;
5) ;
5)  ;
6) ;
6)  ;
7) ;
7)  ;
8) ;
8)  ; ;
| 1)  ;
2) ;
2)  ;
3) ;
3)  ;
4) ;
4)  ;
5) ;
5)  ;
6) ;
6)  ;
7) ;
7) 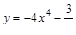 ;
8) ;
8)  . .
|
| 2. Вычислить производную функции, используя правила дифференцирования: | |
1)  ;
2) ;
2)  ;
3) ;
3)  ; ;
| 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
Практическая работа 26.
Цель: проверить умения находить производные от суммы, разности, произведения и частного.
| I вариант | II вариант |
| 1. Контрольные вопросы | |
| а) чему равна производная тригонометрических функций? б) вычислить у ¢, если | |
| 2. Вычислить производную: | |
1) 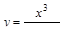 ;
2) ;
2) 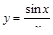 ;
3) ;
3)  ; ;
| 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
| 3. Решить уравнение у ¢=0, если: | |

| 
|
| 4. Решить неравенство у ¢>0, если: | |
1)  ;
2) ;
2)  ; ;
| 1)  ;
2) ;
2)  . .
|
Практическая работа 27.
Цель: проверить умения применять производную к исследованию функций.
| I вариант | II вариант | ||||||||||||||||||
| 1. Контрольные вопросы | |||||||||||||||||||
| а) что такое интервалы монотонности? б) что такое max и min для функции?
в) вспомнить алгоритм исследования функции на экстремумы. | |||||||||||||||||||
| 2. Записать общую схему исследования функции для построения графиков. | |||||||||||||||||||
| 3. Используя данные о производной у ¢, приведённые в таблице, ответить на вопросы: а) промежутки возрастания; б) промежутки убывания; в) точки максимума; г) точки минимума. | |||||||||||||||||||
| I вариант |
| ||||||||||||||||||
| II вариант |
| ||||||||||||||||||
| 4. Используя вышеизложенную схему, исследовать и построить график функции: | |||||||||||||||||||
| 1) 2) | 3) 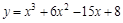 ;
4) ;
4)  . .
| ||||||||||||||||||
Практическая работа 28, 29.
Цель: проверить умение находить наибольшее и наименьшее значение функции на отрезке и применять знания к решению практических задач.
Вариант 1.
№1.Найдите наибольшее и наименьшее значения функции:
а)  на отрезке на отрезке 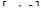 ;
б) ;
б)  на отрезке на отрезке  .
№2.Разбейте число 10 на два положительных слагаемых так, чтобы сумма квадратов этих слагаемых была наименьшей.
№3Периметр равнобедренного треугольника равен 60 см. При каком значении высоты, проведенной к основанию треугольника, площадь треугольника наибольшая? .
№2.Разбейте число 10 на два положительных слагаемых так, чтобы сумма квадратов этих слагаемых была наименьшей.
№3Периметр равнобедренного треугольника равен 60 см. При каком значении высоты, проведенной к основанию треугольника, площадь треугольника наибольшая?
|
Вариант 2.
№1. Найдите наибольшее и наименьшее значения функции
а) 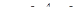 на отрезке на отрезке 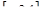 ;
б) ;
б)  на отрезке на отрезке 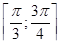 .
№2. Разбейте число 40 на два положительных слагаемых так, чтобы их произведение было наибольшим.
№3. Площадь прямоугольника равна 25 см2 .Найдите наименьший возможный периметр этого прямоугольника. .
№2. Разбейте число 40 на два положительных слагаемых так, чтобы их произведение было наибольшим.
№3. Площадь прямоугольника равна 25 см2 .Найдите наименьший возможный периметр этого прямоугольника.
|
Вариант 3.
№1.Найдите наибольшее и наименьшее значения функции
а)  на отрезке на отрезке  ;
б) ;
б)  на отрезке на отрезке  .
№2.Разбейте число 18 на два положительных слагаемых так, чтобы сумма удвоенного первого слагаемого и квадрата второго слагаемого была наименьшей.
№3. Площадь прямоугольника равна 81 см2. Найдите наименьший возможный периметр этого прямоугольника. .
№2.Разбейте число 18 на два положительных слагаемых так, чтобы сумма удвоенного первого слагаемого и квадрата второго слагаемого была наименьшей.
№3. Площадь прямоугольника равна 81 см2. Найдите наименьший возможный периметр этого прямоугольника.
|
Вариант 4.
№1. Найдите наибольшее и наименьшее значения функции
а) 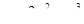 на отрезке на отрезке 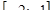 ;
б) ;
б) 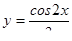 на отрезке на отрезке 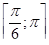 .
№2.Разбейте число 18 на два положительных слагаемых так, чтобы произведение квадрата первого слагаемого и второго слагаемого было наибольшим.
№3.Периметр равнобедренного треугольника равен 20 см. При каком значении боковой стороны площадь треугольника наибольшая? .
№2.Разбейте число 18 на два положительных слагаемых так, чтобы произведение квадрата первого слагаемого и второго слагаемого было наибольшим.
№3.Периметр равнобедренного треугольника равен 20 см. При каком значении боковой стороны площадь треугольника наибольшая?
|
|
|
|
|
|
|





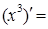
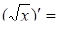



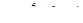 ;
; .
. ;
; ;
;