 |
Контрольная работа по теме «Комбинаторика»
|
|
|
|
1 вариант.
Сколько различных трехзначных чисел можно составить из пяти цифр 1, 2, 3, 4, 5?
Были куплены билеты в театр для шести ребят. Сколькими способами эти ребята могут занять свои места в театре.
У покупателя имелись в кошельке по одной купюре 10 руб., 50 руб., 100 руб. и 500 руб., а у продавца не было денег, чтобы сдать сдачу. Сколько различных товаров мог купить покупатель, чтобы ему не нужно было требовать сдачу (предполагается, что в магазине есть товары на любую сумму, доступную покупателю)?
Шифр пакета, содержащего конкурсные задания, состоит из трех различных букв и последующих 4 цифр (цифры могут повторяться). Сколько может быть различных пакетов, если в них используется 10букв и 5 цифр?
Сколькими способами можно поставить в две одинаковые вазы 8 различных цветков, если в каждой вазе их должно быть нечетное число?
Найти разложение бинома  .
.
2 вариант.
Пять ребят решили поехать за город, но забыли договориться, в какой вагон всем следует садиться, поэтому каждый мог сесть в любой вагон. Сколько существует различных вариантов распределения ребят по вагонам, если в поезде было 10 вагонов?
Учеников попросили нарисовать прямоугольник, разбить его на шесть прямоугольников параллельными отрезками и раскрасить шестью разными красками. Сколько может получится различных раскрасок?
К началу учебного года в магазине покупателям предлагались комплекты тетрадей, альбомы, ручки, линейки, краски и наборы цветных карандашей. Сколько можно было сделать различных покупок, если брать не более одного предмета каждого наименования?
Сколько можно изготовить кодовых замков, у которых код состоит из двух различных цифр и трех любых букв, если можно использовать 10 цифр и 15 букв. Порядок набора цифр и букв не имеет значения.
|
|
|
Сколькими способами можно разложить 10 различных конфет в два одинаковых пакета, если в них должно быть четное число конфет?
Найти разложение бинома  .
.
Внеаудиторная самостоятельная работа
1.Выполнение домашнего задания.
2.Составление примеров применения задач комбинаторики в различных сферах жизни.
Тема 5. Координаты и векторы
Устный опрос
1. Как складываются вектора.
2. Как вектор умножается на число.
3. Как найти длину вектора, зная его координаты.
4. Как найти середину отрезка, зная координаты его концов.
Практическая работа 10.
Цель: проверить умение нахождение вектора по рисунку, разложение вектора через другие, действия с векторами в координатной форме.
Вариант 1
1. Дан параллелепипед ABCDA 1 B 1 C 1 D 1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный: 1) 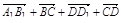 ; 2)
; 2)  .
.
2. DABC – тетраэдр. Точка М – середина ребра ВС, точка N – середина отрезка D М. Выразите вектор  через векторы
через векторы  ,
, 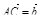 ,
, 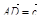 .
.
3. Медианы D BDC пересекаются в точке Р, точка K – середина отрезка AP (точка А не лежит в плоскости BDC). Разложите вектор  по векторам
по векторам  ,
, 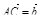 ,
, 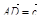 .
.
4. В параллелепипеде ABCDA 1 B 1 C 1 D 1 М лежит на BB 1, причем B М: М B 1 = 3: 4, а Р лежит на B 1 D 1, причем B 1 P: Р D 1 = 2: 1. Разложите вектор 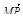 по векторам
по векторам  ,
,  и
и  .
.
5. Даны векторы  {2; –4; 3} и
{2; –4; 3} и 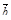 {–3; 1; 1}. Найдите координаты вектора
{–3; 1; 1}. Найдите координаты вектора  =
=  +
+  .
.
6. Даны векторы  {1; –2; 0},
{1; –2; 0}, 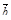 {3; –6; 0} и
{3; –6; 0} и  {0; –3; 4}. Найдите координаты вектора
{0; –3; 4}. Найдите координаты вектора 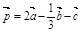 .
.
Вариант 2
1. ABCDA 1 B 1 C 1 D 1 – параллелепипед. Изобразите на рисунке векторы, равные: 1)  ;2)
;2)  .
.
2. В тетраэдре DABC точка N – середина ребра AB, точка P – середина отрезка DN. Выразите вектор  через векторы
через векторы  ,
,  ,
, 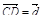 .
.
3. Медианы грани DBC тетраэдра DABC пересекаются в точке О, точка R – середина отрезка AO. Разложите вектор 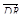 по векторам
по векторам  ,
,  ,
, 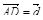 .
.
4. Дан параллелепипед ABCDA 1 B 1 C 1 D 1. Точка М лежит на AB, причем A М: М B = 5: 2, а K Î AD 1, причем AK: К D 1 = 3: 5. Разложите вектор  по векторам
по векторам  ,
,  и
и  .
.
|
|
|
5. Даны векторы  {1; –3; 1} и
{1; –3; 1} и 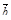 {–1; 2; 2}. Найдите координаты вектора
{–1; 2; 2}. Найдите координаты вектора  =
=  –
–  .
.
6. Даны векторы  {2; 4; –6},
{2; 4; –6}, 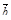 {–3; 1; 0} и
{–3; 1; 0} и  {3; 0; –1}. Найдите координаты вектора
{3; 0; –1}. Найдите координаты вектора  .
.
Вариант 3
1. ABCDA 1 B 1 C 1 D 1 – параллелепипед. Изобразите на рисунке векторы, равные: 1)  ;2)
;2) 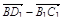
2. Точка S – середина ребра A С тетраэдра DABC, точка N – середина отрезка DS. Выразите вектор  через векторы
через векторы 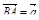 ,
, 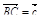 ,
,  .
.
3. В треугольнике KLM точка С – пересечение медиан, T – середина отрезка N С (N не лежит в плоскости KLM). Разложите  по векторам
по векторам  ,
, 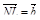 ,
, 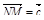 .
.
4. В параллелепипеде ABCDA 1 B 1 C 1 D 1 точка N делит CC 1 так, что CN: NC 1 = 1: 3, а точка H делит A 1 С 1 так, что А 1 Н: НС 1 = 5: 2. Разложите вектор  по векторам
по векторам  ,
, 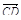 и
и  .
.
5. Даны векторы  {–3; 1; 4} и
{–3; 1; 4} и 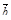 {2; –2; 1}. Найдите координаты вектора
{2; –2; 1}. Найдите координаты вектора  =
=  +
+ 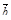 .
.
6. Даны векторы  {8; –4; 2},
{8; –4; 2}, 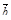 {0; –3; –2} и
{0; –3; –2} и  {2; 0; 1}. Найдите координаты вектора
{2; 0; 1}. Найдите координаты вектора  .
.
Вариант 4
1. Укажите вектор с началом и концом в вершинах параллелепипеда ABCDA 1 B 1 C 1 D 1, равный: 1)  ; 2)
; 2)  .
.
2. Дан тетраэдр DABC. Точка P – середина ребра AB, точка R – середина отрезка CP. Выразите вектор 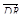 через векторы
через векторы  ,
, 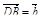 ,
, 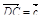 .
.
3. DABC – тетраэдр. Медианы грани DAB пересекаются в точке N, точка O – середина отрезка CN. Разложите вектор 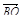 по векторам
по векторам  ,
,  ,
,  .
.
4. ABCDA 1 B 1 C 1 D 1 – параллелепипед. Точка E лежит на ребре DC так, что DE: EC = 1: 4, а F Î С B 1, причем CF: FB 1 =
= 2: 3. Разложите вектор  по векторам
по векторам 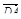 ,
,  и
и  .
.
5. Даны векторы  {–2; 2; 2} и
{–2; 2; 2} и 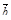 {1; –1; 4}. Найдите координаты вектора
{1; –1; 4}. Найдите координаты вектора  =
=  –
– 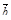 .
.
6. Даны векторы  {3; 2; 0},
{3; 2; 0}, 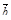 {9; 0; 3} и
{9; 0; 3} и  {2; –5; 4}. Найдите координаты вектора
{2; –5; 4}. Найдите координаты вектора  .
.
Вариант 5
1. ABCDA 1 B 1 C 1 D 1 – параллелепипед. Изобразите на рисунке векторы, равные: 1) 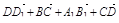 ; 2)
; 2)  .
.
2. На середине ребра ВС тетраэдра DABC лежит точка T, а на середине отрезка DT – точка H. Выразите вектор  через векторы
через векторы  ,
, 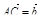 ,
,  .
.
3. R – точка пересечения медиан треугольника SPQ, M – середина отрезка FR (точка F не лежит в плоскости SPQ). Разложите вектор 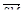 по векторам
по векторам 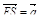 ,
,  ,
,  .
.
4. Точка K лежит на ребре BB 1 параллелепипеда ABCDA 1 B 1 C 1 D 1 так, что BK: KB 1 = 3: 4, а N Î D 1 B 1, причем D 1 N: NB 1 = 1: 2. Разложите вектор  по векторам
по векторам  ,
,  и
и  .
.
5. Даны векторы  {2; 3; –4} и
{2; 3; –4} и 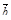 {3; –4; 2}. Найдите координаты вектора
{3; –4; 2}. Найдите координаты вектора  =
=  +
+ 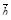 .
.
6. Даны векторы  {4; 3; –1},
{4; 3; –1}, 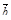 {0; 2; –3} и
{0; 2; –3} и  {–3; 0; 6}. Найдите координаты вектора
{–3; 0; 6}. Найдите координаты вектора  .
.
Вариант 6
1. Дан параллелепипед ABCDA 1 B 1 C 1 D 1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный:
1)  ; 2)
; 2)  .
.
2. DABC – тетраэдр. На середине ребра AB лежит точка К, точка M – середина отрезка DK. Выразите вектор  через векторы
через векторы  ,
, 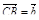 ,
,  .
.
|
|
|
3. В тетраэдре ABCD медианы грани DBC пересекаются в точке E, на середине отрезка AE лежит точка N. Разложите вектор  по векторам
по векторам  ,
,  ,
,  .
.
4. Точка S лежит на ребре BA, а точка Р лежит на диагонали AD 1 параллелепипеда ABCDA 1 B 1 C 1 D 1, BS: SA = 2: 5, AP: Р D 1 = 3: 5. Разложите вектор 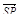 по векторам
по векторам  ,
,  и
и  .
.
5. Даны векторы  {2; –3; 2} и
{2; –3; 2} и 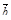 {5; 1; –3}. Найдите координаты вектора
{5; 1; –3}. Найдите координаты вектора 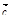 =
=  –
– 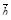 .
.
6. Даны векторы  {0; –3; 2},
{0; –3; 2}, 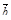 {1; 2; –2} и
{1; 2; –2} и  {6; 4; 0}. Найдите координаты вектора
{6; 4; 0}. Найдите координаты вектора  .
.
Практическая работа 11.
Цель: проверить умение решать математические и прикладные задачи с использованием векторов.
1. Векторы a, b и c заданы декартовыми координатами: а(1; 2; -1), b(3; -1; 7) и c(0; 2; 4). Найдите координаты следующих векторов: а)  ; б)
; б)  в)
в) 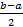 .
.
2. Векторы a, b и c заданы декартовыми координатами: а(1;2;-1), b(3; -1; 7) и c(0; 2; 4). Найдите координаты следующих векторов: а) (ас)b – c (ab); б) (2bb)(b-2c).
3. Докажите, что четырехугольник ABCD – квадрат, если вершины имеют координаты А(-3;5;6), В(1;-5;7), С(8;-3;-1) и D(4;7;-2).
4. Отрезок, концы которого расположены в точках А(-4; 2), В(8; -4), разделен на 4 части. Найдите координаты точек деления.
5. Вычислить работу, произведенную силой F=(6;-3;4), если точка ее приложения, двигаясь прямолинейно, переместилась из А(1;2;3) в В(3;3;3). (F.AB)
Самостоятельная работа 4.
Вариант 1
1. Найдите скалярное произведение  × × 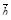 , если: , если:
 2. При каком значении п векторы
2. При каком значении п векторы  (2 п; –3; –6) и (2 п; –3; –6) и 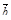 (3; – п; –3) будут перпендикулярными?
3. Найдите угол между векторами (3; – п; –3) будут перпендикулярными?
3. Найдите угол между векторами  (5; –2; 7) и (5; –2; 7) и 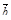 (7; 5; 2). (7; 5; 2).
| Вариант 2
1. Найдите скалярное произведение  × ×  , если: , если:
 2. При каком значении п векторы
2. При каком значении п векторы  (5; 2 п; –3) и (5; 2 п; –3) и 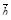 (п; –1; 4) будут перпендикулярными?
3. Найдите угол между векторами (п; –1; 4) будут перпендикулярными?
3. Найдите угол между векторами  (2; 1; 1) и (2; 1; 1) и 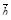 (–1; –1; 0). (–1; –1; 0).
|
Вариант 3
1. Найдите скалярное произведение  × × 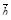 , если: , если:
 2. При каком значении п векторы
2. При каком значении п векторы  (3; –2 п; – п) и (3; –2 п; – п) и 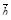 (2; 2; –3) будут перпендикулярными?
3. Найдите угол между векторами (2; 2; –3) будут перпендикулярными?
3. Найдите угол между векторами  (7; 0; –1) и (7; 0; –1) и 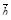 (7; 4; 4). (7; 4; 4).
| Вариант 4
1. Найдите скалярное произведение  × × 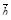 , если: , если:
 2. При каком значении п векторы
2. При каком значении п векторы  (1; –5; 3) и (1; –5; 3) и 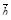 (2 п; –4; –2 п) будут перпендикулярными?
3. Найдите угол между векторами (2 п; –4; –2 п) будут перпендикулярными?
3. Найдите угол между векторами  (7; 2; 1) и (7; 2; 1) и 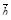 (1; 1; 0). (1; 1; 0).
|
Вариант 5
1. Найдите скалярное произведение  × × 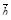 , если: , если:
 2. При каком значении п векторы
2. При каком значении п векторы  (–2 п; 1; –4) и (–2 п; 1; –4) и 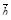 (2; –2 п; –3) будут перпендикулярными?
3. Найдите угол между векторами (2; –2 п; –3) будут перпендикулярными?
3. Найдите угол между векторами  (4; 5; –2) и (4; 5; –2) и 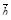 (–7; –5; –4). (–7; –5; –4).
| Вариант 6
1. Найдите скалярное произведение  × × 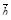 , если: , если:
 2. При каком значении п векторы
2. При каком значении п векторы  (–5 п; 4; –3) и (–5 п; 4; –3) и  (1; –2; – п) будут перпендикулярными?
3. Найдите угол между векторами (1; –2; – п) будут перпендикулярными?
3. Найдите угол между векторами  (–4; 1; 1) и (–4; 1; 1) и 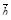 (–1; –1; 0). (–1; –1; 0).
|
Самостоятельная работа 5.
|
|
|
Вариант 1
1. В треугольнике ABC отрезок ВО является медианой.
а) Постройте вектор  , равный сумме векторов
, равный сумме векторов  .
.
б) Докажите, что четырехугольник ВАКС является параллелограммом.
в) Выразите вектор  через векторы
через векторы  .
.
г) Укажите вектор, выходящий из точки В, который является разностью векторов  .
.
2. Даны три точки с координатами: F(8;1;0), E(0;0;4), K(0;5;1).
а) Постройте их в декартовой системе координат.
б) Укажите, в каких координатных плоскостях или на каких координатных осях они находятся.
в) Докажите, что треугольник FKE равнобедренный.
г) Вычислите площадь треугольника FKE с точностью до целых.
Вариант 2.
1. Диагонали прямоугольника ABCD пересекаются в точке О.
а) Постройте вектор  , равный сумме векторов
, равный сумме векторов  .
.
б) Докажите, что четырехугольник OAFD – ромб.
в) Выразите вектор  через векторы
через векторы  .
.
г) Укажите вектор,. Выходящий из точки В, который является разностью векторов  .
.
2. Даны три точки с координатами: Р(4;0;0), К(0;2;0), Т(2;0;4).
а) Постройте их в декартовой системе координат.
б) Укажите, в каких координатных плоскостях или на каких координатных осях они находятся.
в) Докажите, что треугольник РКТ - равнобедренный.
г) Вычислите площадь треугольника РКТ.
|
|
|


