 |
Контрольная работа по теме «Прямые и плоскости в пространстве»
|
|
|
|
1 вариант.
1. Точки А, В, С, D не лежат в одной плоскости. Точки K, L, M, N – середины отрезков АВ, ВC, CD, AD соответственно. Укажите прямые, параллельные прямой АС.
1) KL 2) нет 3) KL и MN 4) MN
2. В тетраэдре ABCD точки K, L, M, N – середины ребер АС, ВС, BD, AD соответственно. Определите вид четырехугольника KLMN и его периметр, если АВ = 16 см и CD = 18 см.
3. Точка О – центр квадрата со стороной, равной 6 см, ОА – отрезок, перпендикулярный к плоскости квадрата и равный 3 см. найдите расстояние от точки А до вершин квадрата.
1) 7 см 2) 5 см 3)3 
см 4) 4 см
4. В треугольнике АВС: АВ = ВС = 25, АС = 48, BD – перпендикуляр к плоскости АВС, BD = 
. Найдите расстояние от точки D до прямой АС.
2 вариант.
1. Точки А, В, С, D не лежат в одной плоскости. Точки K, L, M, N – середины отрезков АВ, ВC, CD, AD соответственно. Укажите прямые, параллельные прямой BD.
1) нет 2) KN и LM 3) KN 4) LM
2. В тетраэдре ABCD точки K, L, M, N – середины ребер АС, ВС, BD, AD соответственно. Определите вид четырехугольника KLMN и его периметр, если АВ = 12 см и CD = 24 см.
3. Точка О – центр квадрата со стороной, равной 4 см, ОА – отрезок, перпендикулярный к плоскости квадрата и равный 2 см. найдите расстояние от точки А до вершин квадрата.
1) 2 см 2) 5 см 3)3 см 4) 4 см
4. В треугольнике АВС: АВ = ВС = 17, АС = 30, BD – перпендикуляр к плоскости АВС, BD = 
. Найдите расстояние от точки D до прямой АС.
Внеаудиторная самостоятельная работа
1.Выполнение домашнего задания.
|
|
|
2.Составить опорный конспект «Стереометрия. Элементы стереометрии. Аксиомы стереометрии и их следствия»
3. Подготовить примеры заданий на доказательство перпендикулярности прямой и плоскости, перпендикулярность плоскостей.
| 1. Составить алгоритмы вычисления угла между прямыми, между плоскостями. 3.Составить алгоритмы вычисления расстояния между скрещивающимися прямыми. |
4.Начертить развёртки многогранников.
5.Создать презентацию на тему «Симметрия в стереометрии»
Тема 4. Комбинаторика
Устный опрос
1. Что такое перестановка?
2. Сколько существует перестановок из 6 букв?
3. Как связаны между собой понятия «размещение» и «перестановка»?
4. Во сколько раз число размещений 10 объектов на четырех местах меньше числа размещений тех же объектов на шести местах?
5. Изобразить треугольник Паскаля.
6. Записать бином Ньютона.
Практическая работа 8.
Цель: проверить умение решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул.
1 вариант
1. Вычислить:
а) 
; б)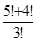 
.
2. Упростить:
а) 
; б) в) 
.
3. Решите задачи:
Учащиеся 9 классов изучают 10 предметов. Сколькими способами можно составить расписание уроков на один день так, чтобы 6 уроков были различными?
(
)
Серия и номер паспорта советского образца состоят из 2-х букв и 6-и цифр. Сколько может быть паспортов с различными сериями и номерами, если римские цифры серии зафиксировать? (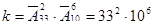
)
Петя, Вася, Галя, Света и Фекла садятся на скамейку. Сколькими способами можно это сделать? (Р5 = 5!)
Сколько слов можно получить, переставляя буквы в словах: сорока, математика?
(
, 
)
На 5 сотрудников выделено 3 путевки в санаторий. Сколькими способами можно распределить эти путевки, если все путевки одинаковые. (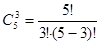
)
У 6 взрослых и 11 детей обнаружены признаки инфекционного заболевания. Чтобы проверить диагноз выбирают 2-х взрослых и 3-х детей для сдачи анализов. Сколькими способами можно это сделать? (
)
|
|
|
В кондитерской продаются пирожные эклер, корзиночка, бисквит, безе, картошка, заварное (всего 6 сортов). Надо купить 10 пирожных. Сколькими способами можно это сделать? (
)
2 вариант
1. Вычислить:
а) 
; б) 
.
2. Упростить:
а)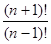 
; б) 
.
3. Решите задачи:
Сколькими способами можно составить трехцветный полосатый флаг, если имеются 5 различных цветов ткани? (
)
Сколькими способами можно разложить 12 различных деталей по трем ящикам?
(
)
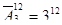Петя, Вася, Галя, Света и Фекла садятся на скамейку. Сколькими способами они могут сесть, чтобы Петя и Фекла были рядом? (
)
Сколькими способами можно разложить 28 различных предметов по 4 различным мешочкам так, чтобы в каждом мешочке было 7 предметов? (
)
Сколькими способами можно разложить в ряд 5 белых и 4 черных шара так, чтобы черные шары не лежали рядом, если: шары одного цвета не отличаются друг от друга, все шары разные. (
; 
)
У одного ученика есть 11 книг по математике, а у другого – 15. Сколькими способами они могут выбрать по 3 книги каждый для обмена? (
)
В почтовым отделении продаются открытки 10 сортов. Сколькими способами можно купить 12 открыток. (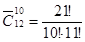
)
Практическая работа 9.
Цель: проверить умение решать задачи с использованием бинома Ньютона и его свойств.
1 вариант
1 Найдите разложения биномов:
а) (х+а)4; б) 
; в) (х+2)5; г) 
.
2. Найдите член, не содержащий х в разложении бинома 
.
3. Дан бином (2a3 + b)n. Найдите n, если сумма всех биномиальных коэффициентов равна 256.
4. С помощью формулы бинома Ньютона вычислите 1013.
2 вариант
1 Найдите разложения биномов:
а) (х-а)4; б) 
; в) (х-2)3; г) 
.
2. Найдите член, не содержащий х в разложении бинома 
.
3. Дан бином (3a-b)n. Найдите n, если сумма всех биномиальных коэффициентов равна 128.
4. С помощью формулы бинома Ньютона вычислите 993.
Тест 2.
1. В трех группах 20, 25 и 30 человек соответственно. Каким количеством способов можно выбрать по одному представителю от каждой группы?
| а | б | в | г |
| 75 | 15000 | 1500 | 150 |
2. Бросаются три шестигранных кубика разных цветов. Сколько различных комбинаций может при этом получится?
| а | б | в | г |
| 36 | 243 | 120 | 216 |
3. Сколькими способами можно набрать подряд четыре различные цифры?
|
|
|
| а | б | в | г |
| 5040 | 10000 | 4536 | 3024 |
4. Сколько анаграмм у слова ОБМОРОК?
| а | б | в | г |
| 140 | 840 | 420 | 120 |
5. В буфете пять чашек и пять блюдец. Каким количеством способов можно выбрать две чашки и два блюдца?
| а | б | в | г |
| 400 | 625 | 100 | 210 |
|
|
|
